Theorem lsmcss 20036

Description: A subset of a pre-Hilbert space whose double orthocomplement has a projection decomposition is a closed subspace. This is the core of the proof that a topologically closed subspace is algebraically closed in a Hilbert space. (Contributed by Mario Carneiro, 13-Oct-2015.)

Hypotheses

Ref	Expression
lsmcss.c	|- C = ( CSubSp ` W )
lsmcss.j	|- V = ( Base ` W )
lsmcss.o	|- ._|_ = ( ocv ` W )
lsmcss.p	|- .(+) = ( LSSum ` W )
lsmcss.1	|- ( ph -> W e. PreHil )
lsmcss.2	|- ( ph -> S C_ V )
lsmcss.3	|- ( ph -> ( ._|_ ` ( ._|_ ` S ) ) C_ ( S .(+) ( ._|_ ` S ) ) )

Assertion

Ref	Expression
lsmcss	|- ( ph -> S e. C )

Proof of Theorem lsmcss

Dummy variables x y z are mutually distinct and distinct from all other variables.

Step	Hyp	Ref	Expression
1		lsmcss.3	. . . . . . 7 |- ( ph -> ( ._|_ ` ( ._|_ ` S ) ) C_ ( S .(+) ( ._|_ ` S ) ) )
2	1	sseld 3602	. . . . . 6 |- ( ph -> ( x e. ( ._|_ ` ( ._|_ ` S ) ) -> x e. ( S .(+) ( ._|_ ` S ) ) ) )
3		lsmcss.1	. . . . . . . 8 |- ( ph -> W e. PreHil )
4		phllmod 19975	. . . . . . . 8 |- ( W e. PreHil -> W e. LMod )
5	3, 4	syl 17	. . . . . . 7 |- ( ph -> W e. LMod )
6		lsmcss.2	. . . . . . 7 |- ( ph -> S C_ V )
7		lsmcss.j	. . . . . . . . 9 |- V = ( Base ` W )
8		lsmcss.o	. . . . . . . . 9 |- ._|_ = ( ocv ` W )
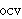9	7, 8	ocvss 20014	. . . . . . . 8 |- ( ._|_ ` S ) C_ V
10	9	a1i 11	. . . . . . 7 |- ( ph -> ( ._|_ ` S ) C_ V )
11		eqid 2622	. . . . . . . 8 |- ( +g ` W ) = ( +g ` W )
12		lsmcss.p	. . . . . . . 8 |- .(+) = ( LSSum ` W )
13	7, 11, 12	lsmelvalx 18055	. . . . . . 7 |- ( ( W e. LMod /\ S C_ V /\ ( ._|_ ` S ) C_ V ) -> ( x e. ( S .(+) ( ._|_ ` S ) ) <-> E. y e. S E. z e. ( ._|_ ` S ) x = ( y ( +g ` W ) z ) ) )
14	5, 6, 10, 13	syl3anc 1326	. . . . . 6 |- ( ph -> ( x e. ( S .(+) ( ._|_ ` S ) ) <-> E. y e. S E. z e. ( ._|_ ` S ) x = ( y ( +g ` W ) z ) ) )
15	2, 14	sylibd 229	. . . . 5 |- ( ph -> ( x e. ( ._|_ ` ( ._|_ ` S ) ) -> E. y e. S E. z e. ( ._|_ ` S ) x = ( y ( +g ` W ) z ) ) )
16	3	ad2antrr 762	. . . . . . . . . . . . . . 15 |- ( ( ( ph /\ ( y e. S /\ z e. ( ._|_ ` S ) ) ) /\ ( y ( +g ` W ) z ) e. ( ._|_ ` ( ._|_ ` S ) ) ) -> W e. PreHil )
17	6	ad2antrr 762	. . . . . . . . . . . . . . . 16 |- ( ( ( ph /\ ( y e. S /\ z e. ( ._|_ ` S ) ) ) /\ ( y ( +g ` W ) z ) e. ( ._|_ ` ( ._|_ ` S ) ) ) -> S C_ V )
18		simplrl 800	. . . . . . . . . . . . . . . 16 |- ( ( ( ph /\ ( y e. S /\ z e. ( ._|_ ` S ) ) ) /\ ( y ( +g ` W ) z ) e. ( ._|_ ` ( ._|_ ` S ) ) ) -> y e. S )
19	17, 18	sseldd 3604	. . . . . . . . . . . . . . 15 |- ( ( ( ph /\ ( y e. S /\ z e. ( ._|_ ` S ) ) ) /\ ( y ( +g ` W ) z ) e. ( ._|_ ` ( ._|_ ` S ) ) ) -> y e. V )
20		simplrr 801	. . . . . . . . . . . . . . . 16 |- ( ( ( ph /\ ( y e. S /\ z e. ( ._|_ ` S ) ) ) /\ ( y ( +g ` W ) z ) e. ( ._|_ ` ( ._|_ ` S ) ) ) -> z e. ( ._|_ ` S ) )
21	9, 20	sseldi 3601	. . . . . . . . . . . . . . 15 |- ( ( ( ph /\ ( y e. S /\ z e. ( ._|_ ` S ) ) ) /\ ( y ( +g ` W ) z ) e. ( ._|_ ` ( ._|_ ` S ) ) ) -> z e. V )
22		eqid 2622	. . . . . . . . . . . . . . . 16 |- (Scalar ` W ) = (Scalar ` W )
23		eqid 2622	. . . . . . . . . . . . . . . 16 |- ( .i ` W ) = ( .i ` W )
24		eqid 2622	. . . . . . . . . . . . . . . 16 |- ( +g ` (Scalar ` W ) ) = ( +g ` (Scalar ` W ) )
25	22, 23, 7, 11, 24	ipdir 19984	. . . . . . . . . . . . . . 15 |- ( ( W e. PreHil /\ ( y e. V /\ z e. V /\ z e. V ) ) -> ( ( y ( +g ` W ) z ) ( .i ` W ) z ) = ( ( y ( .i ` W ) z ) ( +g ` (Scalar ` W ) ) ( z ( .i ` W ) z ) ) )
26	16, 19, 21, 21, 25	syl13anc 1328	. . . . . . . . . . . . . 14 |- ( ( ( ph /\ ( y e. S /\ z e. ( ._|_ ` S ) ) ) /\ ( y ( +g ` W ) z ) e. ( ._|_ ` ( ._|_ ` S ) ) ) -> ( ( y ( +g ` W ) z ) ( .i ` W ) z ) = ( ( y ( .i ` W ) z ) ( +g ` (Scalar ` W ) ) ( z ( .i ` W ) z ) ) )
27		eqid 2622	. . . . . . . . . . . . . . . . . 18 |- ( 0g ` (Scalar ` W ) ) = ( 0g ` (Scalar ` W ) )
28	7, 23, 22, 27, 8	ocvi 20013	. . . . . . . . . . . . . . . . 17 |- ( ( z e. ( ._|_ ` S ) /\ y e. S ) -> ( z ( .i ` W ) y ) = ( 0g ` (Scalar ` W ) ) )
29	20, 18, 28	syl2anc 693	. . . . . . . . . . . . . . . 16 |- ( ( ( ph /\ ( y e. S /\ z e. ( ._|_ ` S ) ) ) /\ ( y ( +g ` W ) z ) e. ( ._|_ ` ( ._|_ ` S ) ) ) -> ( z ( .i ` W ) y ) = ( 0g ` (Scalar ` W ) ) )
30	22, 23, 7, 27	iporthcom 19980	. . . . . . . . . . . . . . . . 17 |- ( ( W e. PreHil /\ z e. V /\ y e. V ) -> ( ( z ( .i ` W ) y ) = ( 0g ` (Scalar ` W ) ) <-> ( y ( .i ` W ) z ) = ( 0g ` (Scalar ` W ) ) ) )
31	16, 21, 19, 30	syl3anc 1326	. . . . . . . . . . . . . . . 16 |- ( ( ( ph /\ ( y e. S /\ z e. ( ._|_ ` S ) ) ) /\ ( y ( +g ` W ) z ) e. ( ._|_ ` ( ._|_ ` S ) ) ) -> ( ( z ( .i ` W ) y ) = ( 0g ` (Scalar ` W ) ) <-> ( y ( .i ` W ) z ) = ( 0g ` (Scalar ` W ) ) ) )
32	29, 31	mpbid 222	. . . . . . . . . . . . . . 15 |- ( ( ( ph /\ ( y e. S /\ z e. ( ._|_ ` S ) ) ) /\ ( y ( +g ` W ) z ) e. ( ._|_ ` ( ._|_ ` S ) ) ) -> ( y ( .i ` W ) z ) = ( 0g ` (Scalar ` W ) ) )
33	32	oveq1d 6665	. . . . . . . . . . . . . 14 |- ( ( ( ph /\ ( y e. S /\ z e. ( ._|_ ` S ) ) ) /\ ( y ( +g ` W ) z ) e. ( ._|_ ` ( ._|_ ` S ) ) ) -> ( ( y ( .i ` W ) z ) ( +g ` (Scalar ` W ) ) ( z ( .i ` W ) z ) ) = ( ( 0g ` (Scalar ` W ) ) ( +g ` (Scalar ` W ) ) ( z ( .i ` W ) z ) ) )
34	16, 4	syl 17	. . . . . . . . . . . . . . . 16 |- ( ( ( ph /\ ( y e. S /\ z e. ( ._|_ ` S ) ) ) /\ ( y ( +g ` W ) z ) e. ( ._|_ ` ( ._|_ ` S ) ) ) -> W e. LMod )
35	22	lmodfgrp 18872	. . . . . . . . . . . . . . . 16 |- ( W e. LMod -> (Scalar ` W ) e. Grp )
36	34, 35	syl 17	. . . . . . . . . . . . . . 15 |- ( ( ( ph /\ ( y e. S /\ z e. ( ._|_ ` S ) ) ) /\ ( y ( +g ` W ) z ) e. ( ._|_ ` ( ._|_ ` S ) ) ) -> (Scalar ` W ) e. Grp )
37		eqid 2622	. . . . . . . . . . . . . . . . 17 |- ( Base ` (Scalar ` W ) ) = ( Base ` (Scalar ` W ) )
38	22, 23, 7, 37	ipcl 19978	. . . . . . . . . . . . . . . 16 |- ( ( W e. PreHil /\ z e. V /\ z e. V ) -> ( z ( .i ` W ) z ) e. ( Base ` (Scalar ` W ) ) )
39	16, 21, 21, 38	syl3anc 1326	. . . . . . . . . . . . . . 15 |- ( ( ( ph /\ ( y e. S /\ z e. ( ._|_ ` S ) ) ) /\ ( y ( +g ` W ) z ) e. ( ._|_ ` ( ._|_ ` S ) ) ) -> ( z ( .i ` W ) z ) e. ( Base ` (Scalar ` W ) ) )
40	37, 24, 27	grplid 17452	. . . . . . . . . . . . . . 15 |- ( ( (Scalar ` W ) e. Grp /\ ( z ( .i ` W ) z ) e. ( Base ` (Scalar ` W ) ) ) -> ( ( 0g ` (Scalar ` W ) ) ( +g ` (Scalar ` W ) ) ( z ( .i ` W ) z ) ) = ( z ( .i ` W ) z ) )
41	36, 39, 40	syl2anc 693	. . . . . . . . . . . . . 14 |- ( ( ( ph /\ ( y e. S /\ z e. ( ._|_ ` S ) ) ) /\ ( y ( +g ` W ) z ) e. ( ._|_ ` ( ._|_ ` S ) ) ) -> ( ( 0g ` (Scalar ` W ) ) ( +g ` (Scalar ` W ) ) ( z ( .i ` W ) z ) ) = ( z ( .i ` W ) z ) )
42	26, 33, 41	3eqtrd 2660	. . . . . . . . . . . . 13 |- ( ( ( ph /\ ( y e. S /\ z e. ( ._|_ ` S ) ) ) /\ ( y ( +g ` W ) z ) e. ( ._|_ ` ( ._|_ ` S ) ) ) -> ( ( y ( +g ` W ) z ) ( .i ` W ) z ) = ( z ( .i ` W ) z ) )
43		simpr 477	. . . . . . . . . . . . . 14 |- ( ( ( ph /\ ( y e. S /\ z e. ( ._|_ ` S ) ) ) /\ ( y ( +g ` W ) z ) e. ( ._|_ ` ( ._|_ ` S ) ) ) -> ( y ( +g ` W ) z ) e. ( ._|_ ` ( ._|_ ` S ) ) )
44	7, 23, 22, 27, 8	ocvi 20013	. . . . . . . . . . . . . 14 |- ( ( ( y ( +g ` W ) z ) e. ( ._|_ ` ( ._|_ ` S ) ) /\ z e. ( ._|_ ` S ) ) -> ( ( y ( +g ` W ) z ) ( .i ` W ) z ) = ( 0g ` (Scalar ` W ) ) )
45	43, 20, 44	syl2anc 693	. . . . . . . . . . . . 13 |- ( ( ( ph /\ ( y e. S /\ z e. ( ._|_ ` S ) ) ) /\ ( y ( +g ` W ) z ) e. ( ._|_ ` ( ._|_ ` S ) ) ) -> ( ( y ( +g ` W ) z ) ( .i ` W ) z ) = ( 0g ` (Scalar ` W ) ) )
46	42, 45	eqtr3d 2658	. . . . . . . . . . . 12 |- ( ( ( ph /\ ( y e. S /\ z e. ( ._|_ ` S ) ) ) /\ ( y ( +g ` W ) z ) e. ( ._|_ ` ( ._|_ ` S ) ) ) -> ( z ( .i ` W ) z ) = ( 0g ` (Scalar ` W ) ) )
47		eqid 2622	. . . . . . . . . . . . . 14 |- ( 0g ` W ) = ( 0g ` W )
48	22, 23, 7, 27, 47	ipeq0 19983	. . . . . . . . . . . . 13 |- ( ( W e. PreHil /\ z e. V ) -> ( ( z ( .i ` W ) z ) = ( 0g ` (Scalar ` W ) ) <-> z = ( 0g ` W ) ) )
49	16, 21, 48	syl2anc 693	. . . . . . . . . . . 12 |- ( ( ( ph /\ ( y e. S /\ z e. ( ._|_ ` S ) ) ) /\ ( y ( +g ` W ) z ) e. ( ._|_ ` ( ._|_ ` S ) ) ) -> ( ( z ( .i ` W ) z ) = ( 0g ` (Scalar ` W ) ) <-> z = ( 0g ` W ) ) )
50	46, 49	mpbid 222	. . . . . . . . . . 11 |- ( ( ( ph /\ ( y e. S /\ z e. ( ._|_ ` S ) ) ) /\ ( y ( +g ` W ) z ) e. ( ._|_ ` ( ._|_ ` S ) ) ) -> z = ( 0g ` W ) )
51	50	oveq2d 6666	. . . . . . . . . 10 |- ( ( ( ph /\ ( y e. S /\ z e. ( ._|_ ` S ) ) ) /\ ( y ( +g ` W ) z ) e. ( ._|_ ` ( ._|_ ` S ) ) ) -> ( y ( +g ` W ) z ) = ( y ( +g ` W ) ( 0g ` W ) ) )
52		lmodgrp 18870	. . . . . . . . . . . . 13 |- ( W e. LMod -> W e. Grp )
53	5, 52	syl 17	. . . . . . . . . . . 12 |- ( ph -> W e. Grp )
54	53	ad2antrr 762	. . . . . . . . . . 11 |- ( ( ( ph /\ ( y e. S /\ z e. ( ._|_ ` S ) ) ) /\ ( y ( +g ` W ) z ) e. ( ._|_ ` ( ._|_ ` S ) ) ) -> W e. Grp )
55	7, 11, 47	grprid 17453	. . . . . . . . . . 11 |- ( ( W e. Grp /\ y e. V ) -> ( y ( +g ` W ) ( 0g ` W ) ) = y )
56	54, 19, 55	syl2anc 693	. . . . . . . . . 10 |- ( ( ( ph /\ ( y e. S /\ z e. ( ._|_ ` S ) ) ) /\ ( y ( +g ` W ) z ) e. ( ._|_ ` ( ._|_ ` S ) ) ) -> ( y ( +g ` W ) ( 0g ` W ) ) = y )
57	51, 56	eqtrd 2656	. . . . . . . . 9 |- ( ( ( ph /\ ( y e. S /\ z e. ( ._|_ ` S ) ) ) /\ ( y ( +g ` W ) z ) e. ( ._|_ ` ( ._|_ ` S ) ) ) -> ( y ( +g ` W ) z ) = y )
58	57, 18	eqeltrd 2701	. . . . . . . 8 |- ( ( ( ph /\ ( y e. S /\ z e. ( ._|_ ` S ) ) ) /\ ( y ( +g ` W ) z ) e. ( ._|_ ` ( ._|_ ` S ) ) ) -> ( y ( +g ` W ) z ) e. S )
59	58	ex 450	. . . . . . 7 |- ( ( ph /\ ( y e. S /\ z e. ( ._|_ ` S ) ) ) -> ( ( y ( +g ` W ) z ) e. ( ._|_ ` ( ._|_ ` S ) ) -> ( y ( +g ` W ) z ) e. S ) )
60		eleq1 2689	. . . . . . . 8 |- ( x = ( y ( +g ` W ) z ) -> ( x e. ( ._|_ ` ( ._|_ ` S ) ) <-> ( y ( +g ` W ) z ) e. ( ._|_ ` ( ._|_ ` S ) ) ) )
61		eleq1 2689	. . . . . . . 8 |- ( x = ( y ( +g ` W ) z ) -> ( x e. S <-> ( y ( +g ` W ) z ) e. S ) )
62	60, 61	imbi12d 334	. . . . . . 7 |- ( x = ( y ( +g ` W ) z ) -> ( ( x e. ( ._|_ ` ( ._|_ ` S ) ) -> x e. S ) <-> ( ( y ( +g ` W ) z ) e. ( ._|_ ` ( ._|_ ` S ) ) -> ( y ( +g ` W ) z ) e. S ) ) )
63	59, 62	syl5ibrcom 237	. . . . . 6 |- ( ( ph /\ ( y e. S /\ z e. ( ._|_ ` S ) ) ) -> ( x = ( y ( +g ` W ) z ) -> ( x e. ( ._|_ ` ( ._|_ ` S ) ) -> x e. S ) ) )
64	63	rexlimdvva 3038	. . . . 5 |- ( ph -> ( E. y e. S E. z e. ( ._|_ ` S ) x = ( y ( +g ` W ) z ) -> ( x e. ( ._|_ ` ( ._|_ ` S ) ) -> x e. S ) ) )
65	15, 64	syld 47	. . . 4 |- ( ph -> ( x e. ( ._|_ ` ( ._|_ ` S ) ) -> ( x e. ( ._|_ ` ( ._|_ ` S ) ) -> x e. S ) ) )
66	65	pm2.43d 53	. . 3 |- ( ph -> ( x e. ( ._|_ ` ( ._|_ ` S ) ) -> x e. S ) )
67	66	ssrdv 3609	. 2 |- ( ph -> ( ._|_ ` ( ._|_ ` S ) ) C_ S )
68		lsmcss.c	. . . 4 |- C = ( CSubSp ` W )
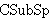69	7, 68, 8	iscss2 20030	. . 3 |- ( ( W e. PreHil /\ S C_ V ) -> ( S e. C <-> ( ._|_ ` ( ._|_ ` S ) ) C_ S ) )
70	3, 6, 69	syl2anc 693	. 2 |- ( ph -> ( S e. C <-> ( ._|_ ` ( ._|_ ` S ) ) C_ S ) )
71	67, 70	mpbird 247	1 |- ( ph -> S e. C )

Syntax hints:   -> wi 4   <-> wb 196   /\ wa 384   = wceq 1483   e. wcel 1990   E.wrex 2913   C_ wss 3574   ` cfv 5888  (class class class)co 6650   Basecbs 15857   +g cplusg 15941  Scalarcsca 15944   .icip 15946   0gc0g 16100   Grpcgrp 17422   LSSumclsm 18049   LModclmod 18863   PreHilcphl 19969   ocvcocv 20004   CSubSpccss 20005

This theorem was proved from axioms:  ax-mp 5  ax-1 6  ax-2 7  ax-3 8  ax-gen 1722  ax-4 1737  ax-5 1839  ax-6 1888  ax-7 1935  ax-8 1992  ax-9 1999  ax-10 2019  ax-11 2034  ax-12 2047  ax-13 2246  ax-ext 2602  ax-rep 4771  ax-sep 4781  ax-nul 4789  ax-pow 4843  ax-pr 4906  ax-un 6949  ax-cnex 9992  ax-resscn 9993  ax-1cn 9994  ax-icn 9995  ax-addcl 9996  ax-addrcl 9997  ax-mulcl 9998  ax-mulrcl 9999  ax-mulcom 10000  ax-addass 10001  ax-mulass 10002  ax-distr 10003  ax-i2m1 10004  ax-1ne0 10005  ax-1rid 10006  ax-rnegex 10007  ax-rrecex 10008  ax-cnre 10009  ax-pre-lttri 10010  ax-pre-lttrn 10011  ax-pre-ltadd 10012  ax-pre-mulgt0 10013

This theorem depends on definitions:  df-bi 197  df-or 385  df-an 386  df-3or 1038  df-3an 1039  df-tru 1486  df-ex 1705  df-nf 1710  df-sb 1881  df-eu 2474  df-mo 2475  df-clab 2609  df-cleq 2615  df-clel 2618  df-nfc 2753  df-ne 2795  df-nel 2898  df-ral 2917  df-rex 2918  df-reu 2919  df-rmo 2920  df-rab 2921  df-v 3202  df-sbc 3436  df-csb 3534  df-dif 3577  df-un 3579  df-in 3581  df-ss 3588  df-pss 3590  df-nul 3916  df-if 4087  df-pw 4160  df-sn 4178  df-pr 4180  df-tp 4182  df-op 4184  df-uni 4437  df-iun 4522  df-br 4654  df-opab 4713  df-mpt 4730  df-tr 4753  df-id 5024  df-eprel 5029  df-po 5035  df-so 5036  df-fr 5073  df-we 5075  df-xp 5120  df-rel 5121  df-cnv 5122  df-co 5123  df-dm 5124  df-rn 5125  df-res 5126  df-ima 5127  df-pred 5680  df-ord 5726  df-on 5727  df-lim 5728  df-suc 5729  df-iota 5851  df-fun 5890  df-fn 5891  df-f 5892  df-f1 5893  df-fo 5894  df-f1o 5895  df-fv 5896  df-riota 6611  df-ov 6653  df-oprab 6654  df-mpt2 6655  df-om 7066  df-1st 7168  df-2nd 7169  df-tpos 7352  df-wrecs 7407  df-recs 7468  df-rdg 7506  df-er 7742  df-map 7859  df-en 7956  df-dom 7957  df-sdom 7958  df-pnf 10076  df-mnf 10077  df-xr 10078  df-ltxr 10079  df-le 10080  df-sub 10268  df-neg 10269  df-nn 11021  df-2 11079  df-3 11080  df-4 11081  df-5 11082  df-6 11083  df-7 11084  df-8 11085  df-ndx 15860  df-slot 15861  df-base 15863  df-sets 15864  df-plusg 15954  df-mulr 15955  df-sca 15957  df-vsca 15958  df-ip 15959  df-0g 16102  df-mgm 17242  df-sgrp 17284  df-mnd 17295  df-mhm 17335  df-grp 17425  df-ghm 17658  df-lsm 18051  df-mgp 18490  df-ur 18502  df-ring 18549  df-oppr 18623  df-rnghom 18715  df-staf 18845  df-srng 18846  df-lmod 18865  df-lmhm 19022  df-lvec 19103  df-sra 19172  df-rgmod 19173  df-phl 19971  df-ocv 20007  df-css 20008

This theorem is referenced by:  pjcss  20060