Theorem pj1lmhm 19100

Description: The left projection function is a linear operator. (Contributed by Mario Carneiro, 15-Oct-2015.) (Revised by Mario Carneiro, 21-Apr-2016.)

Hypotheses

Ref	Expression
pj1lmhm.l	|- L = ( LSubSp ` W )
pj1lmhm.s	|- .(+) = ( LSSum ` W )
pj1lmhm.z	|- .0. = ( 0g ` W )
pj1lmhm.p	|- P = ( proj1 ` W )
pj1lmhm.1	|- ( ph -> W e. LMod )
pj1lmhm.2	|- ( ph -> T e. L )
pj1lmhm.3	|- ( ph -> U e. L )
pj1lmhm.4	|- ( ph -> ( T i^i U ) = { .0. } )

Assertion

Ref	Expression
pj1lmhm	|- ( ph -> ( T P U ) e. ( ( W ↾s ( T .(+) U ) ) LMHom W ) )

Proof of Theorem pj1lmhm

Dummy variables x y are mutually distinct and distinct from all other variables.

Step	Hyp	Ref	Expression
1		eqid 2622	. . 3 |- ( +g ` W ) = ( +g ` W )
2		pj1lmhm.s	. . 3 |- .(+) = ( LSSum ` W )
3		pj1lmhm.z	. . 3 |- .0. = ( 0g ` W )
4		eqid 2622	. . 3 |- (Cntz ` W ) = (Cntz ` W )
5		pj1lmhm.1	. . . . 5 |- ( ph -> W e. LMod )
6		pj1lmhm.l	. . . . . 6 |- L = ( LSubSp ` W )
7	6	lsssssubg 18958	. . . . 5 |- ( W e. LMod -> L C_ (SubGrp ` W ) )
8	5, 7	syl 17	. . . 4 |- ( ph -> L C_ (SubGrp ` W ) )
9		pj1lmhm.2	. . . 4 |- ( ph -> T e. L )
10	8, 9	sseldd 3604	. . 3 |- ( ph -> T e. (SubGrp ` W ) )
11		pj1lmhm.3	. . . 4 |- ( ph -> U e. L )
12	8, 11	sseldd 3604	. . 3 |- ( ph -> U e. (SubGrp ` W ) )
13		pj1lmhm.4	. . 3 |- ( ph -> ( T i^i U ) = { .0. } )
14		lmodabl 18910	. . . . 5 |- ( W e. LMod -> W e. Abel )
15	5, 14	syl 17	. . . 4 |- ( ph -> W e. Abel )
16	4, 15, 10, 12	ablcntzd 18260	. . 3 |- ( ph -> T C_ ( (Cntz ` W ) ` U ) )
17		pj1lmhm.p	. . 3 |- P = ( proj1 ` W )
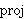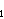18	1, 2, 3, 4, 10, 12, 13, 16, 17	pj1ghm 18116	. 2 |- ( ph -> ( T P U ) e. ( ( W ↾s ( T .(+) U ) ) GrpHom W ) )
19		eqid 2622	. . 3 |- (Scalar ` W ) = (Scalar ` W )
20	19	a1i 11	. 2 |- ( ph -> (Scalar ` W ) = (Scalar ` W ) )
21	1, 2, 3, 4, 10, 12, 13, 16, 17	pj1id 18112	. . . . . . . . 9 |- ( ( ph /\ y e. ( T .(+) U ) ) -> y = ( ( ( T P U ) ` y ) ( +g ` W ) ( ( U P T ) ` y ) ) )
22	21	adantrl 752	. . . . . . . 8 |- ( ( ph /\ ( x e. ( Base ` (Scalar ` W ) ) /\ y e. ( T .(+) U ) ) ) -> y = ( ( ( T P U ) ` y ) ( +g ` W ) ( ( U P T ) ` y ) ) )
23	22	oveq2d 6666	. . . . . . 7 |- ( ( ph /\ ( x e. ( Base ` (Scalar ` W ) ) /\ y e. ( T .(+) U ) ) ) -> ( x ( .s ` W ) y ) = ( x ( .s ` W ) ( ( ( T P U ) ` y ) ( +g ` W ) ( ( U P T ) ` y ) ) ) )
24	5	adantr 481	. . . . . . . 8 |- ( ( ph /\ ( x e. ( Base ` (Scalar ` W ) ) /\ y e. ( T .(+) U ) ) ) -> W e. LMod )
25		simprl 794	. . . . . . . 8 |- ( ( ph /\ ( x e. ( Base ` (Scalar ` W ) ) /\ y e. ( T .(+) U ) ) ) -> x e. ( Base ` (Scalar ` W ) ) )
26	9	adantr 481	. . . . . . . . . 10 |- ( ( ph /\ ( x e. ( Base ` (Scalar ` W ) ) /\ y e. ( T .(+) U ) ) ) -> T e. L )
27		eqid 2622	. . . . . . . . . . 11 |- ( Base ` W ) = ( Base ` W )
28	27, 6	lssss 18937	. . . . . . . . . 10 |- ( T e. L -> T C_ ( Base ` W ) )
29	26, 28	syl 17	. . . . . . . . 9 |- ( ( ph /\ ( x e. ( Base ` (Scalar ` W ) ) /\ y e. ( T .(+) U ) ) ) -> T C_ ( Base ` W ) )
30	10	adantr 481	. . . . . . . . . . 11 |- ( ( ph /\ ( x e. ( Base ` (Scalar ` W ) ) /\ y e. ( T .(+) U ) ) ) -> T e. (SubGrp ` W ) )
31	12	adantr 481	. . . . . . . . . . 11 |- ( ( ph /\ ( x e. ( Base ` (Scalar ` W ) ) /\ y e. ( T .(+) U ) ) ) -> U e. (SubGrp ` W ) )
32	13	adantr 481	. . . . . . . . . . 11 |- ( ( ph /\ ( x e. ( Base ` (Scalar ` W ) ) /\ y e. ( T .(+) U ) ) ) -> ( T i^i U ) = { .0. } )
33	16	adantr 481	. . . . . . . . . . 11 |- ( ( ph /\ ( x e. ( Base ` (Scalar ` W ) ) /\ y e. ( T .(+) U ) ) ) -> T C_ ( (Cntz ` W ) ` U ) )
34	1, 2, 3, 4, 30, 31, 32, 33, 17	pj1f 18110	. . . . . . . . . 10 |- ( ( ph /\ ( x e. ( Base ` (Scalar ` W ) ) /\ y e. ( T .(+) U ) ) ) -> ( T P U ) : ( T .(+) U ) --> T )
35		simprr 796	. . . . . . . . . 10 |- ( ( ph /\ ( x e. ( Base ` (Scalar ` W ) ) /\ y e. ( T .(+) U ) ) ) -> y e. ( T .(+) U ) )
36	34, 35	ffvelrnd 6360	. . . . . . . . 9 |- ( ( ph /\ ( x e. ( Base ` (Scalar ` W ) ) /\ y e. ( T .(+) U ) ) ) -> ( ( T P U ) ` y ) e. T )
37	29, 36	sseldd 3604	. . . . . . . 8 |- ( ( ph /\ ( x e. ( Base ` (Scalar ` W ) ) /\ y e. ( T .(+) U ) ) ) -> ( ( T P U ) ` y ) e. ( Base ` W ) )
38	11	adantr 481	. . . . . . . . . 10 |- ( ( ph /\ ( x e. ( Base ` (Scalar ` W ) ) /\ y e. ( T .(+) U ) ) ) -> U e. L )
39	27, 6	lssss 18937	. . . . . . . . . 10 |- ( U e. L -> U C_ ( Base ` W ) )
40	38, 39	syl 17	. . . . . . . . 9 |- ( ( ph /\ ( x e. ( Base ` (Scalar ` W ) ) /\ y e. ( T .(+) U ) ) ) -> U C_ ( Base ` W ) )
41	1, 2, 3, 4, 30, 31, 32, 33, 17	pj2f 18111	. . . . . . . . . 10 |- ( ( ph /\ ( x e. ( Base ` (Scalar ` W ) ) /\ y e. ( T .(+) U ) ) ) -> ( U P T ) : ( T .(+) U ) --> U )
42	41, 35	ffvelrnd 6360	. . . . . . . . 9 |- ( ( ph /\ ( x e. ( Base ` (Scalar ` W ) ) /\ y e. ( T .(+) U ) ) ) -> ( ( U P T ) ` y ) e. U )
43	40, 42	sseldd 3604	. . . . . . . 8 |- ( ( ph /\ ( x e. ( Base ` (Scalar ` W ) ) /\ y e. ( T .(+) U ) ) ) -> ( ( U P T ) ` y ) e. ( Base ` W ) )
44		eqid 2622	. . . . . . . . 9 |- ( .s ` W ) = ( .s ` W )
45		eqid 2622	. . . . . . . . 9 |- ( Base ` (Scalar ` W ) ) = ( Base ` (Scalar ` W ) )
46	27, 1, 19, 44, 45	lmodvsdi 18886	. . . . . . . 8 |- ( ( W e. LMod /\ ( x e. ( Base ` (Scalar ` W ) ) /\ ( ( T P U ) ` y ) e. ( Base ` W ) /\ ( ( U P T ) ` y ) e. ( Base ` W ) ) ) -> ( x ( .s ` W ) ( ( ( T P U ) ` y ) ( +g ` W ) ( ( U P T ) ` y ) ) ) = ( ( x ( .s ` W ) ( ( T P U ) ` y ) ) ( +g ` W ) ( x ( .s ` W ) ( ( U P T ) ` y ) ) ) )
47	24, 25, 37, 43, 46	syl13anc 1328	. . . . . . 7 |- ( ( ph /\ ( x e. ( Base ` (Scalar ` W ) ) /\ y e. ( T .(+) U ) ) ) -> ( x ( .s ` W ) ( ( ( T P U ) ` y ) ( +g ` W ) ( ( U P T ) ` y ) ) ) = ( ( x ( .s ` W ) ( ( T P U ) ` y ) ) ( +g ` W ) ( x ( .s ` W ) ( ( U P T ) ` y ) ) ) )
48	23, 47	eqtrd 2656	. . . . . 6 |- ( ( ph /\ ( x e. ( Base ` (Scalar ` W ) ) /\ y e. ( T .(+) U ) ) ) -> ( x ( .s ` W ) y ) = ( ( x ( .s ` W ) ( ( T P U ) ` y ) ) ( +g ` W ) ( x ( .s ` W ) ( ( U P T ) ` y ) ) ) )
49	6, 2	lsmcl 19083	. . . . . . . . . 10 |- ( ( W e. LMod /\ T e. L /\ U e. L ) -> ( T .(+) U ) e. L )
50	5, 9, 11, 49	syl3anc 1326	. . . . . . . . 9 |- ( ph -> ( T .(+) U ) e. L )
51	50	adantr 481	. . . . . . . 8 |- ( ( ph /\ ( x e. ( Base ` (Scalar ` W ) ) /\ y e. ( T .(+) U ) ) ) -> ( T .(+) U ) e. L )
52	19, 44, 45, 6	lssvscl 18955	. . . . . . . 8 |- ( ( ( W e. LMod /\ ( T .(+) U ) e. L ) /\ ( x e. ( Base ` (Scalar ` W ) ) /\ y e. ( T .(+) U ) ) ) -> ( x ( .s ` W ) y ) e. ( T .(+) U ) )
53	24, 51, 25, 35, 52	syl22anc 1327	. . . . . . 7 |- ( ( ph /\ ( x e. ( Base ` (Scalar ` W ) ) /\ y e. ( T .(+) U ) ) ) -> ( x ( .s ` W ) y ) e. ( T .(+) U ) )
54	19, 44, 45, 6	lssvscl 18955	. . . . . . . 8 |- ( ( ( W e. LMod /\ T e. L ) /\ ( x e. ( Base ` (Scalar ` W ) ) /\ ( ( T P U ) ` y ) e. T ) ) -> ( x ( .s ` W ) ( ( T P U ) ` y ) ) e. T )
55	24, 26, 25, 36, 54	syl22anc 1327	. . . . . . 7 |- ( ( ph /\ ( x e. ( Base ` (Scalar ` W ) ) /\ y e. ( T .(+) U ) ) ) -> ( x ( .s ` W ) ( ( T P U ) ` y ) ) e. T )
56	19, 44, 45, 6	lssvscl 18955	. . . . . . . 8 |- ( ( ( W e. LMod /\ U e. L ) /\ ( x e. ( Base ` (Scalar ` W ) ) /\ ( ( U P T ) ` y ) e. U ) ) -> ( x ( .s ` W ) ( ( U P T ) ` y ) ) e. U )
57	24, 38, 25, 42, 56	syl22anc 1327	. . . . . . 7 |- ( ( ph /\ ( x e. ( Base ` (Scalar ` W ) ) /\ y e. ( T .(+) U ) ) ) -> ( x ( .s ` W ) ( ( U P T ) ` y ) ) e. U )
58	1, 2, 3, 4, 30, 31, 32, 33, 17, 53, 55, 57	pj1eq 18113	. . . . . 6 |- ( ( ph /\ ( x e. ( Base ` (Scalar ` W ) ) /\ y e. ( T .(+) U ) ) ) -> ( ( x ( .s ` W ) y ) = ( ( x ( .s ` W ) ( ( T P U ) ` y ) ) ( +g ` W ) ( x ( .s ` W ) ( ( U P T ) ` y ) ) ) <-> ( ( ( T P U ) ` ( x ( .s ` W ) y ) ) = ( x ( .s ` W ) ( ( T P U ) ` y ) ) /\ ( ( U P T ) ` ( x ( .s ` W ) y ) ) = ( x ( .s ` W ) ( ( U P T ) ` y ) ) ) ) )
59	48, 58	mpbid 222	. . . . 5 |- ( ( ph /\ ( x e. ( Base ` (Scalar ` W ) ) /\ y e. ( T .(+) U ) ) ) -> ( ( ( T P U ) ` ( x ( .s ` W ) y ) ) = ( x ( .s ` W ) ( ( T P U ) ` y ) ) /\ ( ( U P T ) ` ( x ( .s ` W ) y ) ) = ( x ( .s ` W ) ( ( U P T ) ` y ) ) ) )
60	59	simpld 475	. . . 4 |- ( ( ph /\ ( x e. ( Base ` (Scalar ` W ) ) /\ y e. ( T .(+) U ) ) ) -> ( ( T P U ) ` ( x ( .s ` W ) y ) ) = ( x ( .s ` W ) ( ( T P U ) ` y ) ) )
61	60	ralrimivva 2971	. . 3 |- ( ph -> A. x e. ( Base ` (Scalar ` W ) ) A. y e. ( T .(+) U ) ( ( T P U ) ` ( x ( .s ` W ) y ) ) = ( x ( .s ` W ) ( ( T P U ) ` y ) ) )
62	8, 50	sseldd 3604	. . . . . 6 |- ( ph -> ( T .(+) U ) e. (SubGrp ` W ) )
63		eqid 2622	. . . . . . 7 |- ( W ↾s ( T .(+) U ) ) = ( W ↾s ( T .(+) U ) )
64	63	subgbas 17598	. . . . . 6 |- ( ( T .(+) U ) e. (SubGrp ` W ) -> ( T .(+) U ) = ( Base ` ( W ↾s ( T .(+) U ) ) ) )
65	62, 64	syl 17	. . . . 5 |- ( ph -> ( T .(+) U ) = ( Base ` ( W ↾s ( T .(+) U ) ) ) )
66	65	raleqdv 3144	. . . 4 |- ( ph -> ( A. y e. ( T .(+) U ) ( ( T P U ) ` ( x ( .s ` W ) y ) ) = ( x ( .s ` W ) ( ( T P U ) ` y ) ) <-> A. y e. ( Base ` ( W ↾s ( T .(+) U ) ) ) ( ( T P U ) ` ( x ( .s ` W ) y ) ) = ( x ( .s ` W ) ( ( T P U ) ` y ) ) ) )
67	66	ralbidv 2986	. . 3 |- ( ph -> ( A. x e. ( Base ` (Scalar ` W ) ) A. y e. ( T .(+) U ) ( ( T P U ) ` ( x ( .s ` W ) y ) ) = ( x ( .s ` W ) ( ( T P U ) ` y ) ) <-> A. x e. ( Base ` (Scalar ` W ) ) A. y e. ( Base ` ( W ↾s ( T .(+) U ) ) ) ( ( T P U ) ` ( x ( .s ` W ) y ) ) = ( x ( .s ` W ) ( ( T P U ) ` y ) ) ) )
68	61, 67	mpbid 222	. 2 |- ( ph -> A. x e. ( Base ` (Scalar ` W ) ) A. y e. ( Base ` ( W ↾s ( T .(+) U ) ) ) ( ( T P U ) ` ( x ( .s ` W ) y ) ) = ( x ( .s ` W ) ( ( T P U ) ` y ) ) )
69	63, 6	lsslmod 18960	. . . 4 |- ( ( W e. LMod /\ ( T .(+) U ) e. L ) -> ( W ↾s ( T .(+) U ) ) e. LMod )
70	5, 50, 69	syl2anc 693	. . 3 |- ( ph -> ( W ↾s ( T .(+) U ) ) e. LMod )
71		ovex 6678	. . . . 5 |- ( T .(+) U ) e. _V
72	63, 19	resssca 16031	. . . . 5 |- ( ( T .(+) U ) e. _V -> (Scalar ` W ) = (Scalar ` ( W ↾s ( T .(+) U ) ) ) )
73	71, 72	ax-mp 5	. . . 4 |- (Scalar ` W ) = (Scalar ` ( W ↾s ( T .(+) U ) ) )
74		eqid 2622	. . . 4 |- ( Base ` ( W ↾s ( T .(+) U ) ) ) = ( Base ` ( W ↾s ( T .(+) U ) ) )
75	63, 44	ressvsca 16032	. . . . 5 |- ( ( T .(+) U ) e. _V -> ( .s ` W ) = ( .s ` ( W ↾s ( T .(+) U ) ) ) )
76	71, 75	ax-mp 5	. . . 4 |- ( .s ` W ) = ( .s ` ( W ↾s ( T .(+) U ) ) )
77	73, 19, 45, 74, 76, 44	islmhm3 19028	. . 3 |- ( ( ( W ↾s ( T .(+) U ) ) e. LMod /\ W e. LMod ) -> ( ( T P U ) e. ( ( W ↾s ( T .(+) U ) ) LMHom W ) <-> ( ( T P U ) e. ( ( W ↾s ( T .(+) U ) ) GrpHom W ) /\ (Scalar ` W ) = (Scalar ` W ) /\ A. x e. ( Base ` (Scalar ` W ) ) A. y e. ( Base ` ( W ↾s ( T .(+) U ) ) ) ( ( T P U ) ` ( x ( .s ` W ) y ) ) = ( x ( .s ` W ) ( ( T P U ) ` y ) ) ) ) )
78	70, 5, 77	syl2anc 693	. 2 |- ( ph -> ( ( T P U ) e. ( ( W ↾s ( T .(+) U ) ) LMHom W ) <-> ( ( T P U ) e. ( ( W ↾s ( T .(+) U ) ) GrpHom W ) /\ (Scalar ` W ) = (Scalar ` W ) /\ A. x e. ( Base ` (Scalar ` W ) ) A. y e. ( Base ` ( W ↾s ( T .(+) U ) ) ) ( ( T P U ) ` ( x ( .s ` W ) y ) ) = ( x ( .s ` W ) ( ( T P U ) ` y ) ) ) ) )
79	18, 20, 68, 78	mpbir3and 1245	1 |- ( ph -> ( T P U ) e. ( ( W ↾s ( T .(+) U ) ) LMHom W ) )

Syntax hints:   -> wi 4   <-> wb 196   /\ wa 384   /\ w3a 1037   = wceq 1483   e. wcel 1990   A.wral 2912   _Vcvv 3200   i^i cin 3573   C_ wss 3574   {csn 4177   ` cfv 5888  (class class class)co 6650   Basecbs 15857   ↾_s cress 15858   +g cplusg 15941  Scalarcsca 15944   .scvsca 15945   0gc0g 16100  SubGrpcsubg 17588   GrpHom cghm 17657  Cntzccntz 17748   LSSumclsm 18049   proj1cpj1 18050   Abelcabl 18194   LModclmod 18863   LSubSpclss 18932   LMHom clmhm 19019

This theorem was proved from axioms:  ax-mp 5  ax-1 6  ax-2 7  ax-3 8  ax-gen 1722  ax-4 1737  ax-5 1839  ax-6 1888  ax-7 1935  ax-8 1992  ax-9 1999  ax-10 2019  ax-11 2034  ax-12 2047  ax-13 2246  ax-ext 2602  ax-rep 4771  ax-sep 4781  ax-nul 4789  ax-pow 4843  ax-pr 4906  ax-un 6949  ax-cnex 9992  ax-resscn 9993  ax-1cn 9994  ax-icn 9995  ax-addcl 9996  ax-addrcl 9997  ax-mulcl 9998  ax-mulrcl 9999  ax-mulcom 10000  ax-addass 10001  ax-mulass 10002  ax-distr 10003  ax-i2m1 10004  ax-1ne0 10005  ax-1rid 10006  ax-rnegex 10007  ax-rrecex 10008  ax-cnre 10009  ax-pre-lttri 10010  ax-pre-lttrn 10011  ax-pre-ltadd 10012  ax-pre-mulgt0 10013

This theorem depends on definitions:  df-bi 197  df-or 385  df-an 386  df-3or 1038  df-3an 1039  df-tru 1486  df-ex 1705  df-nf 1710  df-sb 1881  df-eu 2474  df-mo 2475  df-clab 2609  df-cleq 2615  df-clel 2618  df-nfc 2753  df-ne 2795  df-nel 2898  df-ral 2917  df-rex 2918  df-reu 2919  df-rmo 2920  df-rab 2921  df-v 3202  df-sbc 3436  df-csb 3534  df-dif 3577  df-un 3579  df-in 3581  df-ss 3588  df-pss 3590  df-nul 3916  df-if 4087  df-pw 4160  df-sn 4178  df-pr 4180  df-tp 4182  df-op 4184  df-uni 4437  df-iun 4522  df-br 4654  df-opab 4713  df-mpt 4730  df-tr 4753  df-id 5024  df-eprel 5029  df-po 5035  df-so 5036  df-fr 5073  df-we 5075  df-xp 5120  df-rel 5121  df-cnv 5122  df-co 5123  df-dm 5124  df-rn 5125  df-res 5126  df-ima 5127  df-pred 5680  df-ord 5726  df-on 5727  df-lim 5728  df-suc 5729  df-iota 5851  df-fun 5890  df-fn 5891  df-f 5892  df-f1 5893  df-fo 5894  df-f1o 5895  df-fv 5896  df-riota 6611  df-ov 6653  df-oprab 6654  df-mpt2 6655  df-om 7066  df-1st 7168  df-2nd 7169  df-wrecs 7407  df-recs 7468  df-rdg 7506  df-er 7742  df-en 7956  df-dom 7957  df-sdom 7958  df-pnf 10076  df-mnf 10077  df-xr 10078  df-ltxr 10079  df-le 10080  df-sub 10268  df-neg 10269  df-nn 11021  df-2 11079  df-3 11080  df-4 11081  df-5 11082  df-6 11083  df-ndx 15860  df-slot 15861  df-base 15863  df-sets 15864  df-ress 15865  df-plusg 15954  df-sca 15957  df-vsca 15958  df-0g 16102  df-mgm 17242  df-sgrp 17284  df-mnd 17295  df-submnd 17336  df-grp 17425  df-minusg 17426  df-sbg 17427  df-subg 17591  df-ghm 17658  df-cntz 17750  df-lsm 18051  df-pj1 18052  df-cmn 18195  df-abl 18196  df-mgp 18490  df-ur 18502  df-ring 18549  df-lmod 18865  df-lss 18933  df-lmhm 19022

This theorem is referenced by:  pj1lmhm2  19101  pjff  20056