Proof of Theorem btwnconn1lem8
| Step | Hyp | Ref
| Expression |
|---|
| 1 | | simpr2l 1120 |
. . . 4
           
    
                   Cgr Cgr      
              Cgr Cgr            
        Cgr Cgr  
              |
| 2 | 1 | ad2antll 765 |
. . 3
                
                    
                         
                 
        
                                                          
        Cgr Cgr            
        Cgr Cgr           
     
     Cgr Cgr                     Cgr Cgr               
    
               
      Cgr Cgr     
               Cgr Cgr            
        Cgr Cgr  
                |
| 3 | | simpr1r 1119 |
. . . . . 6
           
    
                   Cgr Cgr      
              Cgr Cgr            
        Cgr Cgr  
           Cgr Cgr      |
| 4 | 3 | ad2antll 765 |
. . . . 5
                
                    
                         
                 
        
                                                          
        Cgr Cgr            
        Cgr Cgr           
     
     Cgr Cgr                     Cgr Cgr               
    
               
      Cgr Cgr     
               Cgr Cgr            
        Cgr Cgr  
             Cgr Cgr      |
| 5 | | simp11 1091 |
. . . . . . . 8
                 
                
                                 
            
             
              |
| 6 | | simp2l1 1160 |
. . . . . . . 8
                 
                
                                 
            
             
                  |
| 7 | | simp31 1097 |
. . . . . . . 8
                 
                
                                 
            
             
                  |
| 8 | | simp2r1 1163 |
. . . . . . . 8
                 
                
                                 
            
             
                  |
| 9 | | cgrcomlr 32105 |
. . . . . . . 8
        
        
        
        
              Cgr Cgr           Cgr Cgr       |
| 10 | 5, 6, 7, 6, 8, 9 | syl122anc 1335 |
. . . . . . 7
                 
                
                                 
            
             
                Cgr Cgr  
        Cgr Cgr       |
| 11 | | cgrcom 32097 |
. . . . . . . 8
        
        
                                Cgr Cgr           Cgr Cgr       |
| 12 | 5, 7, 6, 8, 6, 11 | syl122anc 1335 |
. . . . . . 7
                 
                
                                 
            
             
                Cgr Cgr           Cgr Cgr       |
| 13 | 10, 12 | bitrd 268 |
. . . . . 6
                 
                
                                 
            
             
                Cgr Cgr  
        Cgr Cgr       |
| 14 | 13 | adantr 481 |
. . . . 5
                
                    
                         
                 
        
                                                          
        Cgr Cgr            
        Cgr Cgr           
     
     Cgr Cgr                     Cgr Cgr               
    
               
      Cgr Cgr     
               Cgr Cgr            
        Cgr Cgr  
              Cgr Cgr           Cgr Cgr  
    |
| 15 | 4, 14 | mpbid 222 |
. . . 4
                
                    
                         
                 
        
                                                          
        Cgr Cgr            
        Cgr Cgr           
     
     Cgr Cgr                     Cgr Cgr               
    
               
      Cgr Cgr     
               Cgr Cgr            
        Cgr Cgr  
             Cgr Cgr      |
| 16 | | simp33 1099 |
. . . . 5
                 
                
                                 
            
             
                  |
| 17 | | simp2r3 1165 |
. . . . 5
                 
                
                                 
            
             
                  |
| 18 | | simp2l3 1162 |
. . . . . . 7
                 
                
                                 
            
             
                  |
| 19 | | simpr1l 1118 |
. . . . . . . 8
           
    
                   Cgr Cgr      
              Cgr Cgr            
        Cgr Cgr  
              |
| 20 | 19 | ad2antll 765 |
. . . . . . 7
                
                    
                         
                 
        
                                                          
        Cgr Cgr            
        Cgr Cgr           
     
     Cgr Cgr                     Cgr Cgr               
    
               
      Cgr Cgr     
               Cgr Cgr            
        Cgr Cgr  
                |
| 21 | 5, 6, 18, 7, 20 | btwncomand 32122 |
. . . . . 6
                
                    
                         
                 
        
                                                          
        Cgr Cgr            
        Cgr Cgr           
     
     Cgr Cgr                     Cgr Cgr               
    
               
      Cgr Cgr     
               Cgr Cgr            
        Cgr Cgr  
                |
| 22 | | simprll 802 |
. . . . . . 7
                                            
        Cgr Cgr            
        Cgr Cgr           
     
     Cgr Cgr                     Cgr Cgr               
    
               
      Cgr Cgr     
               Cgr Cgr            
        Cgr Cgr  
               |
| 23 | 22 | adantl 482 |
. . . . . 6
                
                    
                         
                 
        
                                                          
        Cgr Cgr            
        Cgr Cgr           
     
     Cgr Cgr                     Cgr Cgr               
    
               
      Cgr Cgr     
               Cgr Cgr            
        Cgr Cgr  
                |
| 24 | | btwnintr 32126 |
. . . . . . . 8
        
        
        
        
                                    |
| 25 | 5, 7, 6, 17, 18, 24 | syl122anc 1335 |
. . . . . . 7
                 
                
                                 
            
             
                   
    
             |
| 26 | 25 | adantr 481 |
. . . . . 6
                
                    
                         
                 
        
                                                          
        Cgr Cgr            
        Cgr Cgr           
     
     Cgr Cgr                     Cgr Cgr               
    
               
      Cgr Cgr     
               Cgr Cgr            
        Cgr Cgr  
                                    |
| 27 | 21, 23, 26 | mp2and 715 |
. . . . 5
                
                    
                         
                 
        
                                                          
        Cgr Cgr            
        Cgr Cgr           
     
     Cgr Cgr                     Cgr Cgr               
    
               
      Cgr Cgr     
               Cgr Cgr            
        Cgr Cgr  
                |
| 28 | | simpr2r 1121 |
. . . . . 6
           
    
                   Cgr Cgr      
              Cgr Cgr            
        Cgr Cgr  
           Cgr Cgr      |
| 29 | 28 | ad2antll 765 |
. . . . 5
                
                    
                         
                 
        
                                                          
        Cgr Cgr            
        Cgr Cgr           
     
     Cgr Cgr                     Cgr Cgr               
    
               
      Cgr Cgr     
               Cgr Cgr            
        Cgr Cgr  
             Cgr Cgr      |
| 30 | 5, 8, 6, 16, 7, 6,
17, 2, 27, 15, 29 | cgrextendand 32116 |
. . . 4
                
                    
                         
                 
        
                                                          
        Cgr Cgr            
        Cgr Cgr           
     
     Cgr Cgr                     Cgr Cgr               
    
               
      Cgr Cgr     
               Cgr Cgr            
        Cgr Cgr  
             Cgr Cgr      |
| 31 | | brcgr3 32153 |
. . . . . 6
                                                 
                    Cgr3 Cgr3         
      Cgr Cgr     
     Cgr Cgr           Cgr Cgr        |
| 32 | 5, 8, 6, 16, 7, 6,
17, 31 | syl133anc 1349 |
. . . . 5
                 
                
                                 
            
             
                    Cgr3 Cgr3         
      Cgr Cgr     
     Cgr Cgr           Cgr Cgr        |
| 33 | 32 | adantr 481 |
. . . 4
                
                    
                         
                 
        
                                                          
        Cgr Cgr            
        Cgr Cgr           
     
     Cgr Cgr                     Cgr Cgr               
    
               
      Cgr Cgr     
               Cgr Cgr            
        Cgr Cgr  
                  Cgr3 Cgr3         
      Cgr Cgr     
     Cgr Cgr           Cgr Cgr        |
| 34 | 15, 30, 29, 33 | mpbir3and 1245 |
. . 3
                
                    
                         
                 
        
                                                          
        Cgr Cgr            
        Cgr Cgr           
     
     Cgr Cgr                     Cgr Cgr               
    
               
      Cgr Cgr     
               Cgr Cgr            
        Cgr Cgr  
                 Cgr3 Cgr3          |
| 35 | 5, 8, 7 | cgrrflx2d 32091 |
. . . . 5
                 
                
                                 
            
             
               Cgr Cgr      |
| 36 | 35 | adantr 481 |
. . . 4
                
                    
                         
                 
        
                                                          
        Cgr Cgr            
        Cgr Cgr           
     
     Cgr Cgr                     Cgr Cgr               
    
               
      Cgr Cgr     
               Cgr Cgr            
        Cgr Cgr  
             Cgr Cgr      |
| 37 | 36, 4 | jca 554 |
. . 3
                
                    
                         
                 
        
                                                          
        Cgr Cgr            
        Cgr Cgr           
     
     Cgr Cgr                     Cgr Cgr               
    
               
      Cgr Cgr     
               Cgr Cgr            
        Cgr Cgr  
              Cgr Cgr           Cgr Cgr       |
| 38 | 2, 34, 37 | 3jca 1242 |
. 2
                
                    
                         
                 
        
                                                          
        Cgr Cgr            
        Cgr Cgr           
     
     Cgr Cgr                     Cgr Cgr               
    
               
      Cgr Cgr     
               Cgr Cgr            
        Cgr Cgr  
                          Cgr3 Cgr3                Cgr Cgr  
        Cgr Cgr  
     |
| 39 | | simp1 1061 |
. . . . 5
                 
                
                                 
            
             
            
         
         |
| 40 | | simp2l 1087 |
. . . . 5
                 
                
                                 
            
             
            
             
         |
| 41 | | simp2r 1088 |
. . . . 5
                 
                
                                 
            
             
                    
               |
| 42 | 39, 40, 41 | 3jca 1242 |
. . . 4
                 
                
                                 
            
             
                         
        
        
                         
                |
| 43 | | simpl 473 |
. . . . 5
                                            
        Cgr Cgr            
        Cgr Cgr           
     
     Cgr Cgr                     Cgr Cgr               
    
               
      Cgr Cgr     
               Cgr Cgr            
        Cgr Cgr  
                                                
        Cgr Cgr            
        Cgr Cgr           
     
     Cgr Cgr                     Cgr Cgr         |
| 44 | | simprl 794 |
. . . . 5
                                            
        Cgr Cgr            
        Cgr Cgr           
     
     Cgr Cgr                     Cgr Cgr               
    
               
      Cgr Cgr     
               Cgr Cgr            
        Cgr Cgr  
               
    
    |
| 45 | 43, 44 | jca 554 |
. . . 4
                                            
        Cgr Cgr            
        Cgr Cgr           
     
     Cgr Cgr                     Cgr Cgr               
    
               
      Cgr Cgr     
               Cgr Cgr            
        Cgr Cgr  
                                                 
        Cgr Cgr            
        Cgr Cgr           
     
     Cgr Cgr                     Cgr Cgr          
      
    
     |
| 46 | | btwnconn1lem7 32200 |
. . . 4
                
                         
                         
                                                    
        Cgr Cgr            
        Cgr Cgr           
     
     Cgr Cgr                     Cgr Cgr          
      
    
          |
| 47 | 42, 45, 46 | syl2an 494 |
. . 3
                
                    
                         
                 
        
                                                          
        Cgr Cgr            
        Cgr Cgr           
     
     Cgr Cgr                     Cgr Cgr               
    
               
      Cgr Cgr     
               Cgr Cgr            
        Cgr Cgr  
            |
| 48 | 47 | necomd 2849 |
. 2
                
                    
                         
                 
        
                                                          
        Cgr Cgr            
        Cgr Cgr           
     
     Cgr Cgr                     Cgr Cgr               
    
               
      Cgr Cgr     
               Cgr Cgr            
        Cgr Cgr  
            |
| 49 | | brofs2 32184 |
. . . . . 6
                 
        
        
                 
             
                        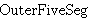                      
          Cgr3 Cgr3                Cgr Cgr  
        Cgr Cgr  
      |
| 50 | 49 | anbi1d 741 |
. . . . 5
                 
        
        
                 
             
                         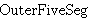              
                        Cgr3 Cgr3                Cgr Cgr           Cgr Cgr              |
| 51 | | 5segofs 32113 |
. . . . 5
                 
        
        
                 
             
                         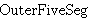              
    
     Cgr Cgr       |
| 52 | 50, 51 | sylbird 250 |
. . . 4
                 
        
        
                 
             
                              Cgr3 Cgr3                Cgr Cgr  
        Cgr Cgr  
               Cgr Cgr       |
| 53 | 5, 8, 6, 16, 7, 7,
6, 17, 8, 52 | syl333anc 1358 |
. . 3
                 
                
                                 
            
             
                              Cgr3 Cgr3                Cgr Cgr  
        Cgr Cgr  
               Cgr Cgr       |
| 54 | 53 | adantr 481 |
. 2
                
                    
                         
                 
        
                                                          
        Cgr Cgr            
        Cgr Cgr           
     
     Cgr Cgr                     Cgr Cgr               
    
               
      Cgr Cgr     
               Cgr Cgr            
        Cgr Cgr  
            
    
          Cgr3 Cgr3                Cgr Cgr  
        Cgr Cgr  
               Cgr Cgr       |
| 55 | 38, 48, 54 | mp2and 715 |
1
                
                    
                         
                 
        
                                                          
        Cgr Cgr            
        Cgr Cgr           
     
     Cgr Cgr                     Cgr Cgr               
    
               
      Cgr Cgr     
               Cgr Cgr            
        Cgr Cgr  
             Cgr Cgr      |