| Step | Hyp | Ref
| Expression |
|---|
| 1 | | simpl 473 |
. . . . . 6
        
        
                 
  |
| 2 | | simpr1 1067 |
. . . . . 6
        
        
                 
      |
| 3 | | simpr2 1068 |
. . . . . 6
        
        
                 
      |
| 4 | | simpr3 1069 |
. . . . . 6
        
        
                 
      |
| 5 | | brsegle2 32216 |
. . . . . 6
        
        
        
        
              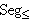        
        
     
     Cgr Cgr        |
| 6 | 1, 2, 3, 2, 4, 5 | syl122anc 1335 |
. . . . 5
        
        
                      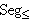         
                   Cgr Cgr        |
| 7 | 6 | adantr 481 |
. . . 4
                                    OutsideOf OutsideOf  
          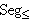        
        
     
     Cgr Cgr        |
| 8 | | simprl 794 |
. . . . . . . . . 10
                         
                     OutsideOf OutsideOf              
     Cgr Cgr          OutsideOf OutsideOf      |
| 9 | | outsideofcom 32235 |
. . . . . . . . . . 11
        
        
                  OutsideOf OutsideOf       OutsideOf OutsideOf       |
| 10 | 9 | ad2antrr 762 |
. . . . . . . . . 10
                         
                     OutsideOf OutsideOf              
     Cgr Cgr           OutsideOf OutsideOf       OutsideOf OutsideOf       |
| 11 | 8, 10 | mpbid 222 |
. . . . . . . . 9
                         
                     OutsideOf OutsideOf              
     Cgr Cgr          OutsideOf OutsideOf      |
| 12 | | simpll 790 |
. . . . . . . . . . 11
                                                |
| 13 | | simplr1 1103 |
. . . . . . . . . . 11
                                                    |
| 14 | | simplr3 1105 |
. . . . . . . . . . 11
                                                    |
| 15 | 12, 13, 14 | cgrrflxd 32095 |
. . . . . . . . . 10
                                                 Cgr Cgr      |
| 16 | 15 | adantr 481 |
. . . . . . . . 9
                         
                     OutsideOf OutsideOf              
     Cgr Cgr              Cgr Cgr  
   |
| 17 | 11, 16 | jca 554 |
. . . . . . . 8
                         
                     OutsideOf OutsideOf              
     Cgr Cgr           OutsideOf OutsideOf           Cgr Cgr       |
| 18 | | simprrl 804 |
. . . . . . . . . . 11
                         
                     OutsideOf OutsideOf              
     Cgr Cgr                 |
| 19 | | simpr 477 |
. . . . . . . . . . . . 13
                                                    |
| 20 | | simplr2 1104 |
. . . . . . . . . . . . 13
                                                    |
| 21 | | btwncolinear1 32176 |
. . . . . . . . . . . . 13
        
        
                        
         |
| 22 | 12, 13, 19, 20, 21 | syl13anc 1328 |
. . . . . . . . . . . 12
                                                              |
| 23 | 22 | adantr 481 |
. . . . . . . . . . 11
                         
                     OutsideOf OutsideOf              
     Cgr Cgr                 
         |
| 24 | 18, 23 | mpd 15 |
. . . . . . . . . 10
                         
                     OutsideOf OutsideOf              
     Cgr Cgr                 |
| 25 | | outsidene1 32230 |
. . . . . . . . . . . . . 14
        
        
                  OutsideOf OutsideOf           |
| 26 | 25 | ad2antrr 762 |
. . . . . . . . . . . . 13
                         
                     OutsideOf OutsideOf              
     Cgr Cgr           OutsideOf OutsideOf           |
| 27 | 8, 26 | mpd 15 |
. . . . . . . . . . . 12
                         
                     OutsideOf OutsideOf              
     Cgr Cgr             |
| 28 | 27 | neneqd 2799 |
. . . . . . . . . . 11
                         
                     OutsideOf OutsideOf              
     Cgr Cgr          
   |
| 29 | | df-3an 1039 |
. . . . . . . . . . . . 13
    OutsideOf OutsideOf           
        Cgr Cgr               
   OutsideOf OutsideOf              
     Cgr Cgr                 |
| 30 | | simpr2l 1120 |
. . . . . . . . . . . . . . 15
                         
                     OutsideOf OutsideOf              
     Cgr Cgr                
    
   |
| 31 | 12, 20, 13, 19, 30 | btwncomand 32122 |
. . . . . . . . . . . . . 14
                         
                     OutsideOf OutsideOf              
     Cgr Cgr                
        |
| 32 | | simpr3 1069 |
. . . . . . . . . . . . . 14
                         
                     OutsideOf OutsideOf              
     Cgr Cgr                
        |
| 33 | | btwnswapid2 32125 |
. . . . . . . . . . . . . . . 16
        
        
                           
            |
| 34 | 12, 20, 19, 13, 33 | syl13anc 1328 |
. . . . . . . . . . . . . . 15
                                                    
               |
| 35 | 34 | adantr 481 |
. . . . . . . . . . . . . 14
                         
                     OutsideOf OutsideOf              
     Cgr Cgr                
                        |
| 36 | 31, 32, 35 | mp2and 715 |
. . . . . . . . . . . . 13
                         
                     OutsideOf OutsideOf              
     Cgr Cgr                
    |
| 37 | 29, 36 | sylan2br 493 |
. . . . . . . . . . . 12
                         
                      OutsideOf OutsideOf           
        Cgr Cgr                 
    |
| 38 | 37 | expr 643 |
. . . . . . . . . . 11
                         
                     OutsideOf OutsideOf              
     Cgr Cgr                
      |
| 39 | 28, 38 | mtod 189 |
. . . . . . . . . 10
                         
                     OutsideOf OutsideOf              
     Cgr Cgr          
       |
| 40 | | broutsideof 32228 |
. . . . . . . . . 10
   OutsideOf OutsideOf                         |
| 41 | 24, 39, 40 | sylanbrc 698 |
. . . . . . . . 9
                         
                     OutsideOf OutsideOf              
     Cgr Cgr          OutsideOf OutsideOf      |
| 42 | | simprrr 805 |
. . . . . . . . 9
                         
                     OutsideOf OutsideOf              
     Cgr Cgr              Cgr Cgr      |
| 43 | 41, 42 | jca 554 |
. . . . . . . 8
                         
                     OutsideOf OutsideOf              
     Cgr Cgr           OutsideOf OutsideOf           Cgr Cgr       |
| 44 | | outsideofeq 32237 |
. . . . . . . . . 10
        
        
                 
             
              OutsideOf OutsideOf     
     Cgr Cgr         OutsideOf OutsideOf           Cgr Cgr       
     |
| 45 | 12, 13, 20, 13, 14, 14, 19, 44 | syl133anc 1349 |
. . . . . . . . 9
                                                OutsideOf OutsideOf     
     Cgr Cgr         OutsideOf OutsideOf           Cgr Cgr       
     |
| 46 | 45 | adantr 481 |
. . . . . . . 8
                         
                     OutsideOf OutsideOf              
     Cgr Cgr             OutsideOf OutsideOf           Cgr Cgr  
      OutsideOf OutsideOf    
      Cgr Cgr             |
| 47 | 17, 43, 46 | mp2and 715 |
. . . . . . 7
                         
                     OutsideOf OutsideOf              
     Cgr Cgr          
  |
| 48 | | opeq2 4403 |
. . . . . . . . 9
                  |
| 49 | 48 | breq2d 4665 |
. . . . . . . 8
                
       |
| 50 | 18, 49 | syl5ibrcom 237 |
. . . . . . 7
                         
                     OutsideOf OutsideOf              
     Cgr Cgr                       |
| 51 | 47, 50 | mpd 15 |
. . . . . 6
                         
                     OutsideOf OutsideOf              
     Cgr Cgr                 |
| 52 | 51 | an4s 869 |
. . . . 5
                         
           OutsideOf OutsideOf  
            
              Cgr Cgr                 |
| 53 | 52 | rexlimdvaa 3032 |
. . . 4
                                    OutsideOf OutsideOf  
                  
        Cgr Cgr                |
| 54 | 7, 53 | sylbid 230 |
. . 3
                                    OutsideOf OutsideOf  
          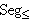                |
| 55 | | btwnsegle 32224 |
. . . 4
        
        
                        
     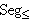        |
| 56 | 55 | adantr 481 |
. . 3
                                    OutsideOf OutsideOf  
         
        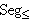   
    |
| 57 | 54, 56 | impbid 202 |
. 2
                                    OutsideOf OutsideOf  
          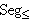        
       |
| 58 | 57 | ex 450 |
1
        
        
                  OutsideOf OutsideOf            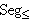        
        |