Theorem funcrngcsetc 41998

Description: The "natural forgetful functor" from the category of non-unital rings into the category of sets which sends each non-unital ring to its underlying set (base set) and the morphisms (non-unital ring homomorphisms) to mappings of the corresponding base sets. An alternate proof is provided in funcrngcsetcALT 41999, using cofuval2 16547 to construct the "natural forgetful functor" from the category of non-unital rings into the category of sets by composing the "inclusion functor" from the category of non-unital rings into the category of extensible structures, see rngcifuestrc 41997, and the "natural forgetful functor" from the category of extensible structures into the category of sets, see funcestrcsetc 16789. (Contributed by AV, 26-Mar-2020.)

Hypotheses

Ref	Expression
funcrngcsetc.r	|- R = (RngCat ` U )
funcrngcsetc.s	|- S = ( SetCat ` U )
funcrngcsetc.b	|- B = ( Base ` R )
funcrngcsetc.u	|- ( ph -> U e. WUni )
funcrngcsetc.f	|- ( ph -> F = ( x e. B |-> ( Base ` x ) ) )
funcrngcsetc.g	|- ( ph -> G = ( x e. B , y e. B |-> ( _I |` ( x RngHomo y ) ) ) )

Assertion

Ref	Expression
funcrngcsetc	|- ( ph -> F ( R Func S ) G )

Distinct variable groups:   x, B, y   x, R, y   x, S   x, U, y   ph, x, y

Allowed substitution hints:   S( y)   F( x, y)   G( x, y)

Proof of Theorem funcrngcsetc

Dummy variables a b f are mutually distinct and distinct from all other variables.

Step	Hyp	Ref	Expression
1		eqid 2622	. . . . . 6 |- (ExtStrCat ` U ) = (ExtStrCat ` U )
2		funcrngcsetc.s	. . . . . 6 |- S = ( SetCat ` U )
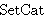3		eqid 2622	. . . . . 6 |- ( Base ` (ExtStrCat ` U ) ) = ( Base ` (ExtStrCat ` U ) )
4		eqid 2622	. . . . . 6 |- ( Base ` S ) = ( Base ` S )
5		funcrngcsetc.u	. . . . . 6 |- ( ph -> U e. WUni )
6	1, 5	estrcbas 16765	. . . . . . 7 |- ( ph -> U = ( Base ` (ExtStrCat ` U ) ) )
7	6	mpteq1d 4738	. . . . . 6 |- ( ph -> ( x e. U |-> ( Base ` x ) ) = ( x e. ( Base ` (ExtStrCat ` U ) ) |-> ( Base ` x ) ) )
8		mpt2eq12 6715	. . . . . . 7 |- ( ( U = ( Base ` (ExtStrCat ` U ) ) /\ U = ( Base ` (ExtStrCat ` U ) ) ) -> ( x e. U , y e. U |-> ( _I |` ( ( Base ` y ) ^m ( Base ` x ) ) ) ) = ( x e. ( Base ` (ExtStrCat ` U ) ) , y e. ( Base ` (ExtStrCat ` U ) ) |-> ( _I |` ( ( Base ` y ) ^m ( Base ` x ) ) ) ) )
9	6, 6, 8	syl2anc 693	. . . . . 6 |- ( ph -> ( x e. U , y e. U |-> ( _I |` ( ( Base ` y ) ^m ( Base ` x ) ) ) ) = ( x e. ( Base ` (ExtStrCat ` U ) ) , y e. ( Base ` (ExtStrCat ` U ) ) |-> ( _I |` ( ( Base ` y ) ^m ( Base ` x ) ) ) ) )
10	1, 2, 3, 4, 5, 7, 9	funcestrcsetc 16789	. . . . 5 |- ( ph -> ( x e. U |-> ( Base ` x ) ) ( (ExtStrCat ` U ) Func S ) ( x e. U , y e. U |-> ( _I |` ( ( Base ` y ) ^m ( Base ` x ) ) ) ) )
11		df-br 4654	. . . . 5 |- ( ( x e. U |-> ( Base ` x ) ) ( (ExtStrCat ` U ) Func S ) ( x e. U , y e. U |-> ( _I |` ( ( Base ` y ) ^m ( Base ` x ) ) ) ) <-> <. ( x e. U |-> ( Base ` x ) ) , ( x e. U , y e. U |-> ( _I |` ( ( Base ` y ) ^m ( Base ` x ) ) ) ) >. e. ( (ExtStrCat ` U ) Func S ) )
12	10, 11	sylib 208	. . . 4 |- ( ph -> <. ( x e. U |-> ( Base ` x ) ) , ( x e. U , y e. U |-> ( _I |` ( ( Base ` y ) ^m ( Base ` x ) ) ) ) >. e. ( (ExtStrCat ` U ) Func S ) )
13		funcrngcsetc.r	. . . . . . 7 |- R = (RngCat ` U )
14		eqid 2622	. . . . . . 7 |- ( Base ` R ) = ( Base ` R )
15	13, 14, 5	rngcbas 41965	. . . . . 6 |- ( ph -> ( Base ` R ) = ( U i^i Rng ) )
16		incom 3805	. . . . . 6 |- ( U i^i Rng ) = (Rng i^i U )
17	15, 16	syl6eq 2672	. . . . 5 |- ( ph -> ( Base ` R ) = (Rng i^i U ) )
18		eqid 2622	. . . . . 6 |- ( Hom ` R ) = ( Hom ` R )
19	13, 14, 5, 18	rngchomfval 41966	. . . . 5 |- ( ph -> ( Hom ` R ) = ( RngHomo |` ( ( Base ` R ) X. ( Base ` R ) ) ) )
20	1, 5, 17, 19	rnghmsubcsetc 41977	. . . 4 |- ( ph -> ( Hom ` R ) e. (Subcat ` (ExtStrCat ` U ) ) )
21	12, 20	funcres 16556	. . 3 |- ( ph -> ( <. ( x e. U |-> ( Base ` x ) ) , ( x e. U , y e. U |-> ( _I |` ( ( Base ` y ) ^m ( Base ` x ) ) ) ) >. |`f ( Hom ` R ) ) e. ( ( (ExtStrCat ` U ) |`cat ( Hom ` R ) ) Func S ) )
22		mptexg 6484	. . . . . 6 |- ( U e. WUni -> ( x e. U |-> ( Base ` x ) ) e. _V )
23	5, 22	syl 17	. . . . 5 |- ( ph -> ( x e. U |-> ( Base ` x ) ) e. _V )
24		fvex 6201	. . . . . 6 |- ( Hom ` R ) e. _V
25	24	a1i 11	. . . . 5 |- ( ph -> ( Hom ` R ) e. _V )
26		mpt2exga 7246	. . . . . 6 |- ( ( U e. WUni /\ U e. WUni ) -> ( x e. U , y e. U |-> ( _I |` ( ( Base ` y ) ^m ( Base ` x ) ) ) ) e. _V )
27	5, 5, 26	syl2anc 693	. . . . 5 |- ( ph -> ( x e. U , y e. U |-> ( _I |` ( ( Base ` y ) ^m ( Base ` x ) ) ) ) e. _V )
28	15, 19	rnghmresfn 41963	. . . . 5 |- ( ph -> ( Hom ` R ) Fn ( ( Base ` R ) X. ( Base ` R ) ) )
29	23, 25, 27, 28	resfval2 16553	. . . 4 |- ( ph -> ( <. ( x e. U |-> ( Base ` x ) ) , ( x e. U , y e. U |-> ( _I |` ( ( Base ` y ) ^m ( Base ` x ) ) ) ) >. |`f ( Hom ` R ) ) = <. ( ( x e. U |-> ( Base ` x ) ) |` ( Base ` R ) ) , ( a e. ( Base ` R ) , b e. ( Base ` R ) |-> ( ( a ( x e. U , y e. U |-> ( _I |` ( ( Base ` y ) ^m ( Base ` x ) ) ) ) b ) |` ( a ( Hom ` R ) b ) ) ) >. )
30		inss1 3833	. . . . . . . 8 |- ( U i^i Rng ) C_ U
31	15, 30	syl6eqss 3655	. . . . . . 7 |- ( ph -> ( Base ` R ) C_ U )
32	31	resmptd 5452	. . . . . 6 |- ( ph -> ( ( x e. U |-> ( Base ` x ) ) |` ( Base ` R ) ) = ( x e. ( Base ` R ) |-> ( Base ` x ) ) )
33		funcrngcsetc.f	. . . . . . 7 |- ( ph -> F = ( x e. B |-> ( Base ` x ) ) )
34		funcrngcsetc.b	. . . . . . . . 9 |- B = ( Base ` R )
35	34	a1i 11	. . . . . . . 8 |- ( ph -> B = ( Base ` R ) )
36	35	mpteq1d 4738	. . . . . . 7 |- ( ph -> ( x e. B |-> ( Base ` x ) ) = ( x e. ( Base ` R ) |-> ( Base ` x ) ) )
37	33, 36	eqtr2d 2657	. . . . . 6 |- ( ph -> ( x e. ( Base ` R ) |-> ( Base ` x ) ) = F )
38	32, 37	eqtrd 2656	. . . . 5 |- ( ph -> ( ( x e. U |-> ( Base ` x ) ) |` ( Base ` R ) ) = F )
39		funcrngcsetc.g	. . . . . 6 |- ( ph -> G = ( x e. B , y e. B |-> ( _I |` ( x RngHomo y ) ) ) )
40		oveq1 6657	. . . . . . . . 9 |- ( x = a -> ( x RngHomo y ) = ( a RngHomo y ) )
41	40	reseq2d 5396	. . . . . . . 8 |- ( x = a -> ( _I |` ( x RngHomo y ) ) = ( _I |` ( a RngHomo y ) ) )
42		oveq2 6658	. . . . . . . . 9 |- ( y = b -> ( a RngHomo y ) = ( a RngHomo b ) )
43	42	reseq2d 5396	. . . . . . . 8 |- ( y = b -> ( _I |` ( a RngHomo y ) ) = ( _I |` ( a RngHomo b ) ) )
44	41, 43	cbvmpt2v 6735	. . . . . . 7 |- ( x e. B , y e. B |-> ( _I |` ( x RngHomo y ) ) ) = ( a e. B , b e. B |-> ( _I |` ( a RngHomo b ) ) )
45	44	a1i 11	. . . . . 6 |- ( ph -> ( x e. B , y e. B |-> ( _I |` ( x RngHomo y ) ) ) = ( a e. B , b e. B |-> ( _I |` ( a RngHomo b ) ) ) )
46	34	a1i 11	. . . . . . 7 |- ( ( ph /\ a e. B ) -> B = ( Base ` R ) )
47		eqidd 2623	. . . . . . . . . 10 |- ( ( ph /\ ( a e. B /\ b e. B ) ) -> ( x e. U , y e. U |-> ( _I |` ( ( Base ` y ) ^m ( Base ` x ) ) ) ) = ( x e. U , y e. U |-> ( _I |` ( ( Base ` y ) ^m ( Base ` x ) ) ) ) )
48		fveq2 6191	. . . . . . . . . . . . 13 |- ( y = b -> ( Base ` y ) = ( Base ` b ) )
49		fveq2 6191	. . . . . . . . . . . . 13 |- ( x = a -> ( Base ` x ) = ( Base ` a ) )
50	48, 49	oveqan12rd 6670	. . . . . . . . . . . 12 |- ( ( x = a /\ y = b ) -> ( ( Base ` y ) ^m ( Base ` x ) ) = ( ( Base ` b ) ^m ( Base ` a ) ) )
51	50	reseq2d 5396	. . . . . . . . . . 11 |- ( ( x = a /\ y = b ) -> ( _I |` ( ( Base ` y ) ^m ( Base ` x ) ) ) = ( _I |` ( ( Base ` b ) ^m ( Base ` a ) ) ) )
52	51	adantl 482	. . . . . . . . . 10 |- ( ( ( ph /\ ( a e. B /\ b e. B ) ) /\ ( x = a /\ y = b ) ) -> ( _I |` ( ( Base ` y ) ^m ( Base ` x ) ) ) = ( _I |` ( ( Base ` b ) ^m ( Base ` a ) ) ) )
53	34, 31	syl5eqss 3649	. . . . . . . . . . . . . 14 |- ( ph -> B C_ U )
54	53	sseld 3602	. . . . . . . . . . . . 13 |- ( ph -> ( a e. B -> a e. U ) )
55	54	com12 32	. . . . . . . . . . . 12 |- ( a e. B -> ( ph -> a e. U ) )
56	55	adantr 481	. . . . . . . . . . 11 |- ( ( a e. B /\ b e. B ) -> ( ph -> a e. U ) )
57	56	impcom 446	. . . . . . . . . 10 |- ( ( ph /\ ( a e. B /\ b e. B ) ) -> a e. U )
58	53	sseld 3602	. . . . . . . . . . . 12 |- ( ph -> ( b e. B -> b e. U ) )
59	58	adantld 483	. . . . . . . . . . 11 |- ( ph -> ( ( a e. B /\ b e. B ) -> b e. U ) )
60	59	imp 445	. . . . . . . . . 10 |- ( ( ph /\ ( a e. B /\ b e. B ) ) -> b e. U )
61		ovexd 6680	. . . . . . . . . . 11 |- ( ( ph /\ ( a e. B /\ b e. B ) ) -> ( ( Base ` b ) ^m ( Base ` a ) ) e. _V )
62	61	resiexd 6480	. . . . . . . . . 10 |- ( ( ph /\ ( a e. B /\ b e. B ) ) -> ( _I |` ( ( Base ` b ) ^m ( Base ` a ) ) ) e. _V )
63	47, 52, 57, 60, 62	ovmpt2d 6788	. . . . . . . . 9 |- ( ( ph /\ ( a e. B /\ b e. B ) ) -> ( a ( x e. U , y e. U |-> ( _I |` ( ( Base ` y ) ^m ( Base ` x ) ) ) ) b ) = ( _I |` ( ( Base ` b ) ^m ( Base ` a ) ) ) )
64	63	reseq1d 5395	. . . . . . . 8 |- ( ( ph /\ ( a e. B /\ b e. B ) ) -> ( ( a ( x e. U , y e. U |-> ( _I |` ( ( Base ` y ) ^m ( Base ` x ) ) ) ) b ) |` ( a ( Hom ` R ) b ) ) = ( ( _I |` ( ( Base ` b ) ^m ( Base ` a ) ) ) |` ( a ( Hom ` R ) b ) ) )
65	5	adantr 481	. . . . . . . . . 10 |- ( ( ph /\ ( a e. B /\ b e. B ) ) -> U e. WUni )
66		simprl 794	. . . . . . . . . 10 |- ( ( ph /\ ( a e. B /\ b e. B ) ) -> a e. B )
67		simprr 796	. . . . . . . . . 10 |- ( ( ph /\ ( a e. B /\ b e. B ) ) -> b e. B )
68	13, 34, 65, 18, 66, 67	rngchom 41967	. . . . . . . . 9 |- ( ( ph /\ ( a e. B /\ b e. B ) ) -> ( a ( Hom ` R ) b ) = ( a RngHomo b ) )
69	68	reseq2d 5396	. . . . . . . 8 |- ( ( ph /\ ( a e. B /\ b e. B ) ) -> ( ( _I |` ( ( Base ` b ) ^m ( Base ` a ) ) ) |` ( a ( Hom ` R ) b ) ) = ( ( _I |` ( ( Base ` b ) ^m ( Base ` a ) ) ) |` ( a RngHomo b ) ) )
70		eqid 2622	. . . . . . . . . . . 12 |- ( Base ` a ) = ( Base ` a )
71		eqid 2622	. . . . . . . . . . . 12 |- ( Base ` b ) = ( Base ` b )
72	70, 71	rnghmf 41899	. . . . . . . . . . 11 |- ( f e. ( a RngHomo b ) -> f : ( Base ` a ) --> ( Base ` b ) )
73		fvex 6201	. . . . . . . . . . . . . 14 |- ( Base ` b ) e. _V
74		fvex 6201	. . . . . . . . . . . . . 14 |- ( Base ` a ) e. _V
75	73, 74	pm3.2i 471	. . . . . . . . . . . . 13 |- ( ( Base ` b ) e. _V /\ ( Base ` a ) e. _V )
76	75	a1i 11	. . . . . . . . . . . 12 |- ( ( ph /\ ( a e. B /\ b e. B ) ) -> ( ( Base ` b ) e. _V /\ ( Base ` a ) e. _V ) )
77		elmapg 7870	. . . . . . . . . . . 12 |- ( ( ( Base ` b ) e. _V /\ ( Base ` a ) e. _V ) -> ( f e. ( ( Base ` b ) ^m ( Base ` a ) ) <-> f : ( Base ` a ) --> ( Base ` b ) ) )
78	76, 77	syl 17	. . . . . . . . . . 11 |- ( ( ph /\ ( a e. B /\ b e. B ) ) -> ( f e. ( ( Base ` b ) ^m ( Base ` a ) ) <-> f : ( Base ` a ) --> ( Base ` b ) ) )
79	72, 78	syl5ibr 236	. . . . . . . . . 10 |- ( ( ph /\ ( a e. B /\ b e. B ) ) -> ( f e. ( a RngHomo b ) -> f e. ( ( Base ` b ) ^m ( Base ` a ) ) ) )
80	79	ssrdv 3609	. . . . . . . . 9 |- ( ( ph /\ ( a e. B /\ b e. B ) ) -> ( a RngHomo b ) C_ ( ( Base ` b ) ^m ( Base ` a ) ) )
81	80	resabs1d 5428	. . . . . . . 8 |- ( ( ph /\ ( a e. B /\ b e. B ) ) -> ( ( _I |` ( ( Base ` b ) ^m ( Base ` a ) ) ) |` ( a RngHomo b ) ) = ( _I |` ( a RngHomo b ) ) )
82	64, 69, 81	3eqtrrd 2661	. . . . . . 7 |- ( ( ph /\ ( a e. B /\ b e. B ) ) -> ( _I |` ( a RngHomo b ) ) = ( ( a ( x e. U , y e. U |-> ( _I |` ( ( Base ` y ) ^m ( Base ` x ) ) ) ) b ) |` ( a ( Hom ` R ) b ) ) )
83	35, 46, 82	mpt2eq123dva 6716	. . . . . 6 |- ( ph -> ( a e. B , b e. B |-> ( _I |` ( a RngHomo b ) ) ) = ( a e. ( Base ` R ) , b e. ( Base ` R ) |-> ( ( a ( x e. U , y e. U |-> ( _I |` ( ( Base ` y ) ^m ( Base ` x ) ) ) ) b ) |` ( a ( Hom ` R ) b ) ) ) )
84	39, 45, 83	3eqtrrd 2661	. . . . 5 |- ( ph -> ( a e. ( Base ` R ) , b e. ( Base ` R ) |-> ( ( a ( x e. U , y e. U |-> ( _I |` ( ( Base ` y ) ^m ( Base ` x ) ) ) ) b ) |` ( a ( Hom ` R ) b ) ) ) = G )
85	38, 84	opeq12d 4410	. . . 4 |- ( ph -> <. ( ( x e. U |-> ( Base ` x ) ) |` ( Base ` R ) ) , ( a e. ( Base ` R ) , b e. ( Base ` R ) |-> ( ( a ( x e. U , y e. U |-> ( _I |` ( ( Base ` y ) ^m ( Base ` x ) ) ) ) b ) |` ( a ( Hom ` R ) b ) ) ) >. = <. F , G >. )
86	29, 85	eqtr2d 2657	. . 3 |- ( ph -> <. F , G >. = ( <. ( x e. U |-> ( Base ` x ) ) , ( x e. U , y e. U |-> ( _I |` ( ( Base ` y ) ^m ( Base ` x ) ) ) ) >. |`f ( Hom ` R ) ) )
87	13, 5, 15, 19	rngcval 41962	. . . 4 |- ( ph -> R = ( (ExtStrCat ` U ) |`cat ( Hom ` R ) ) )
88	87	oveq1d 6665	. . 3 |- ( ph -> ( R Func S ) = ( ( (ExtStrCat ` U ) |`cat ( Hom ` R ) ) Func S ) )
89	21, 86, 88	3eltr4d 2716	. 2 |- ( ph -> <. F , G >. e. ( R Func S ) )
90		df-br 4654	. 2 |- ( F ( R Func S ) G <-> <. F , G >. e. ( R Func S ) )
91	89, 90	sylibr 224	1 |- ( ph -> F ( R Func S ) G )

Syntax hints:   -> wi 4   <-> wb 196   /\ wa 384   = wceq 1483   e. wcel 1990   _Vcvv 3200   i^i cin 3573   <.cop 4183   class class class wbr 4653   |-> cmpt 4729   _I cid 5023   |` cres 5116   -->wf 5884   ` cfv 5888  (class class class)co 6650   |-> cmpt2 6652   ^m cmap 7857  WUnicwun 9522   Basecbs 15857   Hom chom 15952   |`<sub>cat</sub> cresc 16468   Func cfunc 16514   |`_f cresf 16517   SetCatcsetc 16725  ExtStrCatcestrc 16762  Rngcrng 41874   RngHomo crngh 41885  RngCatcrngc 41957

This theorem was proved from axioms:  ax-mp 5  ax-1 6  ax-2 7  ax-3 8  ax-gen 1722  ax-4 1737  ax-5 1839  ax-6 1888  ax-7 1935  ax-8 1992  ax-9 1999  ax-10 2019  ax-11 2034  ax-12 2047  ax-13 2246  ax-ext 2602  ax-rep 4771  ax-sep 4781  ax-nul 4789  ax-pow 4843  ax-pr 4906  ax-un 6949  ax-cnex 9992  ax-resscn 9993  ax-1cn 9994  ax-icn 9995  ax-addcl 9996  ax-addrcl 9997  ax-mulcl 9998  ax-mulrcl 9999  ax-mulcom 10000  ax-addass 10001  ax-mulass 10002  ax-distr 10003  ax-i2m1 10004  ax-1ne0 10005  ax-1rid 10006  ax-rnegex 10007  ax-rrecex 10008  ax-cnre 10009  ax-pre-lttri 10010  ax-pre-lttrn 10011  ax-pre-ltadd 10012  ax-pre-mulgt0 10013

This theorem depends on definitions:  df-bi 197  df-or 385  df-an 386  df-3or 1038  df-3an 1039  df-tru 1486  df-fal 1489  df-ex 1705  df-nf 1710  df-sb 1881  df-eu 2474  df-mo 2475  df-clab 2609  df-cleq 2615  df-clel 2618  df-nfc 2753  df-ne 2795  df-nel 2898  df-ral 2917  df-rex 2918  df-reu 2919  df-rmo 2920  df-rab 2921  df-v 3202  df-sbc 3436  df-csb 3534  df-dif 3577  df-un 3579  df-in 3581  df-ss 3588  df-pss 3590  df-nul 3916  df-if 4087  df-pw 4160  df-sn 4178  df-pr 4180  df-tp 4182  df-op 4184  df-uni 4437  df-int 4476  df-iun 4522  df-br 4654  df-opab 4713  df-mpt 4730  df-tr 4753  df-id 5024  df-eprel 5029  df-po 5035  df-so 5036  df-fr 5073  df-we 5075  df-xp 5120  df-rel 5121  df-cnv 5122  df-co 5123  df-dm 5124  df-rn 5125  df-res 5126  df-ima 5127  df-pred 5680  df-ord 5726  df-on 5727  df-lim 5728  df-suc 5729  df-iota 5851  df-fun 5890  df-fn 5891  df-f 5892  df-f1 5893  df-fo 5894  df-f1o 5895  df-fv 5896  df-riota 6611  df-ov 6653  df-oprab 6654  df-mpt2 6655  df-om 7066  df-1st 7168  df-2nd 7169  df-wrecs 7407  df-recs 7468  df-rdg 7506  df-1o 7560  df-oadd 7564  df-er 7742  df-map 7859  df-pm 7860  df-ixp 7909  df-en 7956  df-dom 7957  df-sdom 7958  df-fin 7959  df-wun 9524  df-pnf 10076  df-mnf 10077  df-xr 10078  df-ltxr 10079  df-le 10080  df-sub 10268  df-neg 10269  df-nn 11021  df-2 11079  df-3 11080  df-4 11081  df-5 11082  df-6 11083  df-7 11084  df-8 11085  df-9 11086  df-n0 11293  df-z 11378  df-dec 11494  df-uz 11688  df-fz 12327  df-struct 15859  df-ndx 15860  df-slot 15861  df-base 15863  df-sets 15864  df-ress 15865  df-plusg 15954  df-hom 15966  df-cco 15967  df-0g 16102  df-cat 16329  df-cid 16330  df-homf 16331  df-ssc 16470  df-resc 16471  df-subc 16472  df-func 16518  df-resf 16521  df-setc 16726  df-estrc 16763  df-mgm 17242  df-sgrp 17284  df-mnd 17295  df-mhm 17335  df-grp 17425  df-ghm 17658  df-abl 18196  df-mgp 18490  df-mgmhm 41779  df-rng0 41875  df-rnghomo 41887  df-rngc 41959

This theorem is referenced by: (None)