Theorem obselocv 20072

Description: A basis element is in the orthocomplement of a subset of the basis iff it is not in the subset. (Contributed by Mario Carneiro, 23-Oct-2015.)

Hypothesis

Ref	Expression
obselocv.o	|- ._|_ = ( ocv ` W )

Assertion

Ref	Expression
obselocv	|- ( ( B e. (OBasis ` W ) /\ C C_ B /\ A e. B ) -> ( A e. ( ._|_ ` C ) <-> -. A e. C ) )

Proof of Theorem obselocv

Dummy variable x is distinct from all other variables.

Step	Hyp	Ref	Expression
1		eqid 2622	. . . . . . 7 |- ( 0g ` W ) = ( 0g ` W )
2	1	obsne0 20069	. . . . . 6 |- ( ( B e. (OBasis ` W ) /\ A e. B ) -> A =/= ( 0g ` W ) )
3	2	3adant2 1080	. . . . 5 |- ( ( B e. (OBasis ` W ) /\ C C_ B /\ A e. B ) -> A =/= ( 0g ` W ) )
4		elin 3796	. . . . . . . 8 |- ( A e. ( C i^i ( ._|_ ` C ) ) <-> ( A e. C /\ A e. ( ._|_ ` C ) ) )
5		obsrcl 20067	. . . . . . . . . . . . . 14 |- ( B e. (OBasis ` W ) -> W e. PreHil )
6	5	3ad2ant1 1082	. . . . . . . . . . . . 13 |- ( ( B e. (OBasis ` W ) /\ C C_ B /\ A e. B ) -> W e. PreHil )
7		phllmod 19975	. . . . . . . . . . . . 13 |- ( W e. PreHil -> W e. LMod )
8	6, 7	syl 17	. . . . . . . . . . . 12 |- ( ( B e. (OBasis ` W ) /\ C C_ B /\ A e. B ) -> W e. LMod )
9		simp2 1062	. . . . . . . . . . . . 13 |- ( ( B e. (OBasis ` W ) /\ C C_ B /\ A e. B ) -> C C_ B )
10		eqid 2622	. . . . . . . . . . . . . . 15 |- ( Base ` W ) = ( Base ` W )
11	10	obsss 20068	. . . . . . . . . . . . . 14 |- ( B e. (OBasis ` W ) -> B C_ ( Base ` W ) )
12	11	3ad2ant1 1082	. . . . . . . . . . . . 13 |- ( ( B e. (OBasis ` W ) /\ C C_ B /\ A e. B ) -> B C_ ( Base ` W ) )
13	9, 12	sstrd 3613	. . . . . . . . . . . 12 |- ( ( B e. (OBasis ` W ) /\ C C_ B /\ A e. B ) -> C C_ ( Base ` W ) )
14		eqid 2622	. . . . . . . . . . . . 13 |- ( LSpan ` W ) = ( LSpan ` W )
15	10, 14	lspssid 18985	. . . . . . . . . . . 12 |- ( ( W e. LMod /\ C C_ ( Base ` W ) ) -> C C_ ( ( LSpan ` W ) ` C ) )
16	8, 13, 15	syl2anc 693	. . . . . . . . . . 11 |- ( ( B e. (OBasis ` W ) /\ C C_ B /\ A e. B ) -> C C_ ( ( LSpan ` W ) ` C ) )
17		ssrin 3838	. . . . . . . . . . 11 |- ( C C_ ( ( LSpan ` W ) ` C ) -> ( C i^i ( ._|_ ` C ) ) C_ ( ( ( LSpan ` W ) ` C ) i^i ( ._|_ ` C ) ) )
18	16, 17	syl 17	. . . . . . . . . 10 |- ( ( B e. (OBasis ` W ) /\ C C_ B /\ A e. B ) -> ( C i^i ( ._|_ ` C ) ) C_ ( ( ( LSpan ` W ) ` C ) i^i ( ._|_ ` C ) ) )
19		obselocv.o	. . . . . . . . . . . . . 14 |- ._|_ = ( ocv ` W )
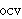20	10, 19, 14	ocvlsp 20020	. . . . . . . . . . . . 13 |- ( ( W e. PreHil /\ C C_ ( Base ` W ) ) -> ( ._|_ ` ( ( LSpan ` W ) ` C ) ) = ( ._|_ ` C ) )
21	6, 13, 20	syl2anc 693	. . . . . . . . . . . 12 |- ( ( B e. (OBasis ` W ) /\ C C_ B /\ A e. B ) -> ( ._|_ ` ( ( LSpan ` W ) ` C ) ) = ( ._|_ ` C ) )
22	21	ineq2d 3814	. . . . . . . . . . 11 |- ( ( B e. (OBasis ` W ) /\ C C_ B /\ A e. B ) -> ( ( ( LSpan ` W ) ` C ) i^i ( ._|_ ` ( ( LSpan ` W ) ` C ) ) ) = ( ( ( LSpan ` W ) ` C ) i^i ( ._|_ ` C ) ) )
23		eqid 2622	. . . . . . . . . . . . . 14 |- ( LSubSp ` W ) = ( LSubSp ` W )
24	10, 23, 14	lspcl 18976	. . . . . . . . . . . . 13 |- ( ( W e. LMod /\ C C_ ( Base ` W ) ) -> ( ( LSpan ` W ) ` C ) e. ( LSubSp ` W ) )
25	8, 13, 24	syl2anc 693	. . . . . . . . . . . 12 |- ( ( B e. (OBasis ` W ) /\ C C_ B /\ A e. B ) -> ( ( LSpan ` W ) ` C ) e. ( LSubSp ` W ) )
26	19, 23, 1	ocvin 20018	. . . . . . . . . . . 12 |- ( ( W e. PreHil /\ ( ( LSpan ` W ) ` C ) e. ( LSubSp ` W ) ) -> ( ( ( LSpan ` W ) ` C ) i^i ( ._|_ ` ( ( LSpan ` W ) ` C ) ) ) = { ( 0g ` W ) } )
27	6, 25, 26	syl2anc 693	. . . . . . . . . . 11 |- ( ( B e. (OBasis ` W ) /\ C C_ B /\ A e. B ) -> ( ( ( LSpan ` W ) ` C ) i^i ( ._|_ ` ( ( LSpan ` W ) ` C ) ) ) = { ( 0g ` W ) } )
28	22, 27	eqtr3d 2658	. . . . . . . . . 10 |- ( ( B e. (OBasis ` W ) /\ C C_ B /\ A e. B ) -> ( ( ( LSpan ` W ) ` C ) i^i ( ._|_ ` C ) ) = { ( 0g ` W ) } )
29	18, 28	sseqtrd 3641	. . . . . . . . 9 |- ( ( B e. (OBasis ` W ) /\ C C_ B /\ A e. B ) -> ( C i^i ( ._|_ ` C ) ) C_ { ( 0g ` W ) } )
30	29	sseld 3602	. . . . . . . 8 |- ( ( B e. (OBasis ` W ) /\ C C_ B /\ A e. B ) -> ( A e. ( C i^i ( ._|_ ` C ) ) -> A e. { ( 0g ` W ) } ) )
31	4, 30	syl5bir 233	. . . . . . 7 |- ( ( B e. (OBasis ` W ) /\ C C_ B /\ A e. B ) -> ( ( A e. C /\ A e. ( ._|_ ` C ) ) -> A e. { ( 0g ` W ) } ) )
32		elsni 4194	. . . . . . 7 |- ( A e. { ( 0g ` W ) } -> A = ( 0g ` W ) )
33	31, 32	syl6 35	. . . . . 6 |- ( ( B e. (OBasis ` W ) /\ C C_ B /\ A e. B ) -> ( ( A e. C /\ A e. ( ._|_ ` C ) ) -> A = ( 0g ` W ) ) )
34	33	necon3ad 2807	. . . . 5 |- ( ( B e. (OBasis ` W ) /\ C C_ B /\ A e. B ) -> ( A =/= ( 0g ` W ) -> -. ( A e. C /\ A e. ( ._|_ ` C ) ) ) )
35	3, 34	mpd 15	. . . 4 |- ( ( B e. (OBasis ` W ) /\ C C_ B /\ A e. B ) -> -. ( A e. C /\ A e. ( ._|_ ` C ) ) )
36		imnan 438	. . . 4 |- ( ( A e. C -> -. A e. ( ._|_ ` C ) ) <-> -. ( A e. C /\ A e. ( ._|_ ` C ) ) )
37	35, 36	sylibr 224	. . 3 |- ( ( B e. (OBasis ` W ) /\ C C_ B /\ A e. B ) -> ( A e. C -> -. A e. ( ._|_ ` C ) ) )
38	37	con2d 129	. 2 |- ( ( B e. (OBasis ` W ) /\ C C_ B /\ A e. B ) -> ( A e. ( ._|_ ` C ) -> -. A e. C ) )
39		simpr 477	. . . . . . 7 |- ( ( ( B e. (OBasis ` W ) /\ C C_ B /\ A e. B ) /\ x e. C ) -> x e. C )
40		eleq1 2689	. . . . . . 7 |- ( A = x -> ( A e. C <-> x e. C ) )
41	39, 40	syl5ibrcom 237	. . . . . 6 |- ( ( ( B e. (OBasis ` W ) /\ C C_ B /\ A e. B ) /\ x e. C ) -> ( A = x -> A e. C ) )
42	41	con3d 148	. . . . 5 |- ( ( ( B e. (OBasis ` W ) /\ C C_ B /\ A e. B ) /\ x e. C ) -> ( -. A e. C -> -. A = x ) )
43		simpl1 1064	. . . . . . 7 |- ( ( ( B e. (OBasis ` W ) /\ C C_ B /\ A e. B ) /\ x e. C ) -> B e. (OBasis ` W ) )
44		simpl3 1066	. . . . . . 7 |- ( ( ( B e. (OBasis ` W ) /\ C C_ B /\ A e. B ) /\ x e. C ) -> A e. B )
45	9	sselda 3603	. . . . . . 7 |- ( ( ( B e. (OBasis ` W ) /\ C C_ B /\ A e. B ) /\ x e. C ) -> x e. B )
46		eqid 2622	. . . . . . . 8 |- ( .i ` W ) = ( .i ` W )
47		eqid 2622	. . . . . . . 8 |- (Scalar ` W ) = (Scalar ` W )
48		eqid 2622	. . . . . . . 8 |- ( 1r ` (Scalar ` W ) ) = ( 1r ` (Scalar ` W ) )
49		eqid 2622	. . . . . . . 8 |- ( 0g ` (Scalar ` W ) ) = ( 0g ` (Scalar ` W ) )
50	10, 46, 47, 48, 49	obsip 20065	. . . . . . 7 |- ( ( B e. (OBasis ` W ) /\ A e. B /\ x e. B ) -> ( A ( .i ` W ) x ) = if ( A = x , ( 1r ` (Scalar ` W ) ) , ( 0g ` (Scalar ` W ) ) ) )
51	43, 44, 45, 50	syl3anc 1326	. . . . . 6 |- ( ( ( B e. (OBasis ` W ) /\ C C_ B /\ A e. B ) /\ x e. C ) -> ( A ( .i ` W ) x ) = if ( A = x , ( 1r ` (Scalar ` W ) ) , ( 0g ` (Scalar ` W ) ) ) )
52		iffalse 4095	. . . . . . 7 |- ( -. A = x -> if ( A = x , ( 1r ` (Scalar ` W ) ) , ( 0g ` (Scalar ` W ) ) ) = ( 0g ` (Scalar ` W ) ) )
53	52	eqeq2d 2632	. . . . . 6 |- ( -. A = x -> ( ( A ( .i ` W ) x ) = if ( A = x , ( 1r ` (Scalar ` W ) ) , ( 0g ` (Scalar ` W ) ) ) <-> ( A ( .i ` W ) x ) = ( 0g ` (Scalar ` W ) ) ) )
54	51, 53	syl5ibcom 235	. . . . 5 |- ( ( ( B e. (OBasis ` W ) /\ C C_ B /\ A e. B ) /\ x e. C ) -> ( -. A = x -> ( A ( .i ` W ) x ) = ( 0g ` (Scalar ` W ) ) ) )
55	42, 54	syld 47	. . . 4 |- ( ( ( B e. (OBasis ` W ) /\ C C_ B /\ A e. B ) /\ x e. C ) -> ( -. A e. C -> ( A ( .i ` W ) x ) = ( 0g ` (Scalar ` W ) ) ) )
56	55	ralrimdva 2969	. . 3 |- ( ( B e. (OBasis ` W ) /\ C C_ B /\ A e. B ) -> ( -. A e. C -> A. x e. C ( A ( .i ` W ) x ) = ( 0g ` (Scalar ` W ) ) ) )
57		simp3 1063	. . . . 5 |- ( ( B e. (OBasis ` W ) /\ C C_ B /\ A e. B ) -> A e. B )
58	12, 57	sseldd 3604	. . . 4 |- ( ( B e. (OBasis ` W ) /\ C C_ B /\ A e. B ) -> A e. ( Base ` W ) )
59	10, 46, 47, 49, 19	elocv 20012	. . . . . 6 |- ( A e. ( ._|_ ` C ) <-> ( C C_ ( Base ` W ) /\ A e. ( Base ` W ) /\ A. x e. C ( A ( .i ` W ) x ) = ( 0g ` (Scalar ` W ) ) ) )
60		df-3an 1039	. . . . . 6 |- ( ( C C_ ( Base ` W ) /\ A e. ( Base ` W ) /\ A. x e. C ( A ( .i ` W ) x ) = ( 0g ` (Scalar ` W ) ) ) <-> ( ( C C_ ( Base ` W ) /\ A e. ( Base ` W ) ) /\ A. x e. C ( A ( .i ` W ) x ) = ( 0g ` (Scalar ` W ) ) ) )
61	59, 60	bitri 264	. . . . 5 |- ( A e. ( ._|_ ` C ) <-> ( ( C C_ ( Base ` W ) /\ A e. ( Base ` W ) ) /\ A. x e. C ( A ( .i ` W ) x ) = ( 0g ` (Scalar ` W ) ) ) )
62	61	baib 944	. . . 4 |- ( ( C C_ ( Base ` W ) /\ A e. ( Base ` W ) ) -> ( A e. ( ._|_ ` C ) <-> A. x e. C ( A ( .i ` W ) x ) = ( 0g ` (Scalar ` W ) ) ) )
63	13, 58, 62	syl2anc 693	. . 3 |- ( ( B e. (OBasis ` W ) /\ C C_ B /\ A e. B ) -> ( A e. ( ._|_ ` C ) <-> A. x e. C ( A ( .i ` W ) x ) = ( 0g ` (Scalar ` W ) ) ) )
64	56, 63	sylibrd 249	. 2 |- ( ( B e. (OBasis ` W ) /\ C C_ B /\ A e. B ) -> ( -. A e. C -> A e. ( ._|_ ` C ) ) )
65	38, 64	impbid 202	1 |- ( ( B e. (OBasis ` W ) /\ C C_ B /\ A e. B ) -> ( A e. ( ._|_ ` C ) <-> -. A e. C ) )

Syntax hints:   -. wn 3   -> wi 4   <-> wb 196   /\ wa 384   /\ w3a 1037   = wceq 1483   e. wcel 1990   =/= wne 2794   A.wral 2912   i^i cin 3573   C_ wss 3574   ifcif 4086   {csn 4177   ` cfv 5888  (class class class)co 6650   Basecbs 15857  Scalarcsca 15944   .icip 15946   0gc0g 16100   1rcur 18501   LModclmod 18863   LSubSpclss 18932   LSpanclspn 18971   PreHilcphl 19969   ocvcocv 20004  OBasiscobs 20046

This theorem was proved from axioms:  ax-mp 5  ax-1 6  ax-2 7  ax-3 8  ax-gen 1722  ax-4 1737  ax-5 1839  ax-6 1888  ax-7 1935  ax-8 1992  ax-9 1999  ax-10 2019  ax-11 2034  ax-12 2047  ax-13 2246  ax-ext 2602  ax-rep 4771  ax-sep 4781  ax-nul 4789  ax-pow 4843  ax-pr 4906  ax-un 6949  ax-cnex 9992  ax-resscn 9993  ax-1cn 9994  ax-icn 9995  ax-addcl 9996  ax-addrcl 9997  ax-mulcl 9998  ax-mulrcl 9999  ax-mulcom 10000  ax-addass 10001  ax-mulass 10002  ax-distr 10003  ax-i2m1 10004  ax-1ne0 10005  ax-1rid 10006  ax-rnegex 10007  ax-rrecex 10008  ax-cnre 10009  ax-pre-lttri 10010  ax-pre-lttrn 10011  ax-pre-ltadd 10012  ax-pre-mulgt0 10013

This theorem depends on definitions:  df-bi 197  df-or 385  df-an 386  df-3or 1038  df-3an 1039  df-tru 1486  df-ex 1705  df-nf 1710  df-sb 1881  df-eu 2474  df-mo 2475  df-clab 2609  df-cleq 2615  df-clel 2618  df-nfc 2753  df-ne 2795  df-nel 2898  df-ral 2917  df-rex 2918  df-reu 2919  df-rmo 2920  df-rab 2921  df-v 3202  df-sbc 3436  df-csb 3534  df-dif 3577  df-un 3579  df-in 3581  df-ss 3588  df-pss 3590  df-nul 3916  df-if 4087  df-pw 4160  df-sn 4178  df-pr 4180  df-tp 4182  df-op 4184  df-uni 4437  df-int 4476  df-iun 4522  df-br 4654  df-opab 4713  df-mpt 4730  df-tr 4753  df-id 5024  df-eprel 5029  df-po 5035  df-so 5036  df-fr 5073  df-we 5075  df-xp 5120  df-rel 5121  df-cnv 5122  df-co 5123  df-dm 5124  df-rn 5125  df-res 5126  df-ima 5127  df-pred 5680  df-ord 5726  df-on 5727  df-lim 5728  df-suc 5729  df-iota 5851  df-fun 5890  df-fn 5891  df-f 5892  df-f1 5893  df-fo 5894  df-f1o 5895  df-fv 5896  df-riota 6611  df-ov 6653  df-oprab 6654  df-mpt2 6655  df-om 7066  df-1st 7168  df-2nd 7169  df-tpos 7352  df-wrecs 7407  df-recs 7468  df-rdg 7506  df-er 7742  df-map 7859  df-en 7956  df-dom 7957  df-sdom 7958  df-pnf 10076  df-mnf 10077  df-xr 10078  df-ltxr 10079  df-le 10080  df-sub 10268  df-neg 10269  df-nn 11021  df-2 11079  df-3 11080  df-4 11081  df-5 11082  df-6 11083  df-7 11084  df-8 11085  df-ndx 15860  df-slot 15861  df-base 15863  df-sets 15864  df-plusg 15954  df-mulr 15955  df-sca 15957  df-vsca 15958  df-ip 15959  df-0g 16102  df-mgm 17242  df-sgrp 17284  df-mnd 17295  df-mhm 17335  df-grp 17425  df-minusg 17426  df-sbg 17427  df-ghm 17658  df-mgp 18490  df-ur 18502  df-ring 18549  df-oppr 18623  df-dvdsr 18641  df-unit 18642  df-rnghom 18715  df-drng 18749  df-staf 18845  df-srng 18846  df-lmod 18865  df-lss 18933  df-lsp 18972  df-lmhm 19022  df-lvec 19103  df-sra 19172  df-rgmod 19173  df-phl 19971  df-ocv 20007  df-obs 20049

This theorem is referenced by:  obs2ss  20073  obslbs  20074