Theorem ocvlss 20016

Description: The orthocomplement of a subset is a linear subspace of the pre-Hilbert space. (Contributed by Mario Carneiro, 13-Oct-2015.)

Hypotheses

Ref	Expression
ocvss.v	|- V = ( Base ` W )
ocvss.o	|- ._|_ = ( ocv ` W )
ocvlss.l	|- L = ( LSubSp ` W )

Assertion

Ref	Expression
ocvlss	|- ( ( W e. PreHil /\ S C_ V ) -> ( ._|_ ` S ) e. L )

Proof of Theorem ocvlss

Dummy variables x r y z are mutually distinct and distinct from all other variables.

Step	Hyp	Ref	Expression
1		ocvss.v	. . . 4 |- V = ( Base ` W )
2		ocvss.o	. . . 4 |- ._|_ = ( ocv ` W )
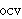3	1, 2	ocvss 20014	. . 3 |- ( ._|_ ` S ) C_ V
4	3	a1i 11	. 2 |- ( ( W e. PreHil /\ S C_ V ) -> ( ._|_ ` S ) C_ V )
5		simpr 477	. . . 4 |- ( ( W e. PreHil /\ S C_ V ) -> S C_ V )
6		phllmod 19975	. . . . . 6 |- ( W e. PreHil -> W e. LMod )
7	6	adantr 481	. . . . 5 |- ( ( W e. PreHil /\ S C_ V ) -> W e. LMod )
8		eqid 2622	. . . . . 6 |- ( 0g ` W ) = ( 0g ` W )
9	1, 8	lmod0vcl 18892	. . . . 5 |- ( W e. LMod -> ( 0g ` W ) e. V )
10	7, 9	syl 17	. . . 4 |- ( ( W e. PreHil /\ S C_ V ) -> ( 0g ` W ) e. V )
11		simpll 790	. . . . . 6 |- ( ( ( W e. PreHil /\ S C_ V ) /\ x e. S ) -> W e. PreHil )
12	5	sselda 3603	. . . . . 6 |- ( ( ( W e. PreHil /\ S C_ V ) /\ x e. S ) -> x e. V )
13		eqid 2622	. . . . . . 7 |- (Scalar ` W ) = (Scalar ` W )
14		eqid 2622	. . . . . . 7 |- ( .i ` W ) = ( .i ` W )
15		eqid 2622	. . . . . . 7 |- ( 0g ` (Scalar ` W ) ) = ( 0g ` (Scalar ` W ) )
16	13, 14, 1, 15, 8	ip0l 19981	. . . . . 6 |- ( ( W e. PreHil /\ x e. V ) -> ( ( 0g ` W ) ( .i ` W ) x ) = ( 0g ` (Scalar ` W ) ) )
17	11, 12, 16	syl2anc 693	. . . . 5 |- ( ( ( W e. PreHil /\ S C_ V ) /\ x e. S ) -> ( ( 0g ` W ) ( .i ` W ) x ) = ( 0g ` (Scalar ` W ) ) )
18	17	ralrimiva 2966	. . . 4 |- ( ( W e. PreHil /\ S C_ V ) -> A. x e. S ( ( 0g ` W ) ( .i ` W ) x ) = ( 0g ` (Scalar ` W ) ) )
19	1, 14, 13, 15, 2	elocv 20012	. . . 4 |- ( ( 0g ` W ) e. ( ._|_ ` S ) <-> ( S C_ V /\ ( 0g ` W ) e. V /\ A. x e. S ( ( 0g ` W ) ( .i ` W ) x ) = ( 0g ` (Scalar ` W ) ) ) )
20	5, 10, 18, 19	syl3anbrc 1246	. . 3 |- ( ( W e. PreHil /\ S C_ V ) -> ( 0g ` W ) e. ( ._|_ ` S ) )
21		ne0i 3921	. . 3 |- ( ( 0g ` W ) e. ( ._|_ ` S ) -> ( ._|_ ` S ) =/= (/) )
22	20, 21	syl 17	. 2 |- ( ( W e. PreHil /\ S C_ V ) -> ( ._|_ ` S ) =/= (/) )
23	5	adantr 481	. . . 4 |- ( ( ( W e. PreHil /\ S C_ V ) /\ ( r e. ( Base ` (Scalar ` W ) ) /\ y e. ( ._|_ ` S ) /\ z e. ( ._|_ ` S ) ) ) -> S C_ V )
24	7	adantr 481	. . . . 5 |- ( ( ( W e. PreHil /\ S C_ V ) /\ ( r e. ( Base ` (Scalar ` W ) ) /\ y e. ( ._|_ ` S ) /\ z e. ( ._|_ ` S ) ) ) -> W e. LMod )
25		simpr1 1067	. . . . . 6 |- ( ( ( W e. PreHil /\ S C_ V ) /\ ( r e. ( Base ` (Scalar ` W ) ) /\ y e. ( ._|_ ` S ) /\ z e. ( ._|_ ` S ) ) ) -> r e. ( Base ` (Scalar ` W ) ) )
26		simpr2 1068	. . . . . . 7 |- ( ( ( W e. PreHil /\ S C_ V ) /\ ( r e. ( Base ` (Scalar ` W ) ) /\ y e. ( ._|_ ` S ) /\ z e. ( ._|_ ` S ) ) ) -> y e. ( ._|_ ` S ) )
27	3, 26	sseldi 3601	. . . . . 6 |- ( ( ( W e. PreHil /\ S C_ V ) /\ ( r e. ( Base ` (Scalar ` W ) ) /\ y e. ( ._|_ ` S ) /\ z e. ( ._|_ ` S ) ) ) -> y e. V )
28		eqid 2622	. . . . . . 7 |- ( .s ` W ) = ( .s ` W )
29		eqid 2622	. . . . . . 7 |- ( Base ` (Scalar ` W ) ) = ( Base ` (Scalar ` W ) )
30	1, 13, 28, 29	lmodvscl 18880	. . . . . 6 |- ( ( W e. LMod /\ r e. ( Base ` (Scalar ` W ) ) /\ y e. V ) -> ( r ( .s ` W ) y ) e. V )
31	24, 25, 27, 30	syl3anc 1326	. . . . 5 |- ( ( ( W e. PreHil /\ S C_ V ) /\ ( r e. ( Base ` (Scalar ` W ) ) /\ y e. ( ._|_ ` S ) /\ z e. ( ._|_ ` S ) ) ) -> ( r ( .s ` W ) y ) e. V )
32		simpr3 1069	. . . . . 6 |- ( ( ( W e. PreHil /\ S C_ V ) /\ ( r e. ( Base ` (Scalar ` W ) ) /\ y e. ( ._|_ ` S ) /\ z e. ( ._|_ ` S ) ) ) -> z e. ( ._|_ ` S ) )
33	3, 32	sseldi 3601	. . . . 5 |- ( ( ( W e. PreHil /\ S C_ V ) /\ ( r e. ( Base ` (Scalar ` W ) ) /\ y e. ( ._|_ ` S ) /\ z e. ( ._|_ ` S ) ) ) -> z e. V )
34		eqid 2622	. . . . . 6 |- ( +g ` W ) = ( +g ` W )
35	1, 34	lmodvacl 18877	. . . . 5 |- ( ( W e. LMod /\ ( r ( .s ` W ) y ) e. V /\ z e. V ) -> ( ( r ( .s ` W ) y ) ( +g ` W ) z ) e. V )
36	24, 31, 33, 35	syl3anc 1326	. . . 4 |- ( ( ( W e. PreHil /\ S C_ V ) /\ ( r e. ( Base ` (Scalar ` W ) ) /\ y e. ( ._|_ ` S ) /\ z e. ( ._|_ ` S ) ) ) -> ( ( r ( .s ` W ) y ) ( +g ` W ) z ) e. V )
37	11	adantlr 751	. . . . . . 7 |- ( ( ( ( W e. PreHil /\ S C_ V ) /\ ( r e. ( Base ` (Scalar ` W ) ) /\ y e. ( ._|_ ` S ) /\ z e. ( ._|_ ` S ) ) ) /\ x e. S ) -> W e. PreHil )
38	31	adantr 481	. . . . . . 7 |- ( ( ( ( W e. PreHil /\ S C_ V ) /\ ( r e. ( Base ` (Scalar ` W ) ) /\ y e. ( ._|_ ` S ) /\ z e. ( ._|_ ` S ) ) ) /\ x e. S ) -> ( r ( .s ` W ) y ) e. V )
39	33	adantr 481	. . . . . . 7 |- ( ( ( ( W e. PreHil /\ S C_ V ) /\ ( r e. ( Base ` (Scalar ` W ) ) /\ y e. ( ._|_ ` S ) /\ z e. ( ._|_ ` S ) ) ) /\ x e. S ) -> z e. V )
40	12	adantlr 751	. . . . . . 7 |- ( ( ( ( W e. PreHil /\ S C_ V ) /\ ( r e. ( Base ` (Scalar ` W ) ) /\ y e. ( ._|_ ` S ) /\ z e. ( ._|_ ` S ) ) ) /\ x e. S ) -> x e. V )
41		eqid 2622	. . . . . . . 8 |- ( +g ` (Scalar ` W ) ) = ( +g ` (Scalar ` W ) )
42	13, 14, 1, 34, 41	ipdir 19984	. . . . . . 7 |- ( ( W e. PreHil /\ ( ( r ( .s ` W ) y ) e. V /\ z e. V /\ x e. V ) ) -> ( ( ( r ( .s ` W ) y ) ( +g ` W ) z ) ( .i ` W ) x ) = ( ( ( r ( .s ` W ) y ) ( .i ` W ) x ) ( +g ` (Scalar ` W ) ) ( z ( .i ` W ) x ) ) )
43	37, 38, 39, 40, 42	syl13anc 1328	. . . . . 6 |- ( ( ( ( W e. PreHil /\ S C_ V ) /\ ( r e. ( Base ` (Scalar ` W ) ) /\ y e. ( ._|_ ` S ) /\ z e. ( ._|_ ` S ) ) ) /\ x e. S ) -> ( ( ( r ( .s ` W ) y ) ( +g ` W ) z ) ( .i ` W ) x ) = ( ( ( r ( .s ` W ) y ) ( .i ` W ) x ) ( +g ` (Scalar ` W ) ) ( z ( .i ` W ) x ) ) )
44	25	adantr 481	. . . . . . . . 9 |- ( ( ( ( W e. PreHil /\ S C_ V ) /\ ( r e. ( Base ` (Scalar ` W ) ) /\ y e. ( ._|_ ` S ) /\ z e. ( ._|_ ` S ) ) ) /\ x e. S ) -> r e. ( Base ` (Scalar ` W ) ) )
45	27	adantr 481	. . . . . . . . 9 |- ( ( ( ( W e. PreHil /\ S C_ V ) /\ ( r e. ( Base ` (Scalar ` W ) ) /\ y e. ( ._|_ ` S ) /\ z e. ( ._|_ ` S ) ) ) /\ x e. S ) -> y e. V )
46		eqid 2622	. . . . . . . . . 10 |- ( .r ` (Scalar ` W ) ) = ( .r ` (Scalar ` W ) )
47	13, 14, 1, 29, 28, 46	ipass 19990	. . . . . . . . 9 |- ( ( W e. PreHil /\ ( r e. ( Base ` (Scalar ` W ) ) /\ y e. V /\ x e. V ) ) -> ( ( r ( .s ` W ) y ) ( .i ` W ) x ) = ( r ( .r ` (Scalar ` W ) ) ( y ( .i ` W ) x ) ) )
48	37, 44, 45, 40, 47	syl13anc 1328	. . . . . . . 8 |- ( ( ( ( W e. PreHil /\ S C_ V ) /\ ( r e. ( Base ` (Scalar ` W ) ) /\ y e. ( ._|_ ` S ) /\ z e. ( ._|_ ` S ) ) ) /\ x e. S ) -> ( ( r ( .s ` W ) y ) ( .i ` W ) x ) = ( r ( .r ` (Scalar ` W ) ) ( y ( .i ` W ) x ) ) )
49	1, 14, 13, 15, 2	ocvi 20013	. . . . . . . . . 10 |- ( ( y e. ( ._|_ ` S ) /\ x e. S ) -> ( y ( .i ` W ) x ) = ( 0g ` (Scalar ` W ) ) )
50	26, 49	sylan 488	. . . . . . . . 9 |- ( ( ( ( W e. PreHil /\ S C_ V ) /\ ( r e. ( Base ` (Scalar ` W ) ) /\ y e. ( ._|_ ` S ) /\ z e. ( ._|_ ` S ) ) ) /\ x e. S ) -> ( y ( .i ` W ) x ) = ( 0g ` (Scalar ` W ) ) )
51	50	oveq2d 6666	. . . . . . . 8 |- ( ( ( ( W e. PreHil /\ S C_ V ) /\ ( r e. ( Base ` (Scalar ` W ) ) /\ y e. ( ._|_ ` S ) /\ z e. ( ._|_ ` S ) ) ) /\ x e. S ) -> ( r ( .r ` (Scalar ` W ) ) ( y ( .i ` W ) x ) ) = ( r ( .r ` (Scalar ` W ) ) ( 0g ` (Scalar ` W ) ) ) )
52	24	adantr 481	. . . . . . . . . 10 |- ( ( ( ( W e. PreHil /\ S C_ V ) /\ ( r e. ( Base ` (Scalar ` W ) ) /\ y e. ( ._|_ ` S ) /\ z e. ( ._|_ ` S ) ) ) /\ x e. S ) -> W e. LMod )
53	13	lmodring 18871	. . . . . . . . . 10 |- ( W e. LMod -> (Scalar ` W ) e. Ring )
54	52, 53	syl 17	. . . . . . . . 9 |- ( ( ( ( W e. PreHil /\ S C_ V ) /\ ( r e. ( Base ` (Scalar ` W ) ) /\ y e. ( ._|_ ` S ) /\ z e. ( ._|_ ` S ) ) ) /\ x e. S ) -> (Scalar ` W ) e. Ring )
55	29, 46, 15	ringrz 18588	. . . . . . . . 9 |- ( ( (Scalar ` W ) e. Ring /\ r e. ( Base ` (Scalar ` W ) ) ) -> ( r ( .r ` (Scalar ` W ) ) ( 0g ` (Scalar ` W ) ) ) = ( 0g ` (Scalar ` W ) ) )
56	54, 44, 55	syl2anc 693	. . . . . . . 8 |- ( ( ( ( W e. PreHil /\ S C_ V ) /\ ( r e. ( Base ` (Scalar ` W ) ) /\ y e. ( ._|_ ` S ) /\ z e. ( ._|_ ` S ) ) ) /\ x e. S ) -> ( r ( .r ` (Scalar ` W ) ) ( 0g ` (Scalar ` W ) ) ) = ( 0g ` (Scalar ` W ) ) )
57	48, 51, 56	3eqtrd 2660	. . . . . . 7 |- ( ( ( ( W e. PreHil /\ S C_ V ) /\ ( r e. ( Base ` (Scalar ` W ) ) /\ y e. ( ._|_ ` S ) /\ z e. ( ._|_ ` S ) ) ) /\ x e. S ) -> ( ( r ( .s ` W ) y ) ( .i ` W ) x ) = ( 0g ` (Scalar ` W ) ) )
58	1, 14, 13, 15, 2	ocvi 20013	. . . . . . . 8 |- ( ( z e. ( ._|_ ` S ) /\ x e. S ) -> ( z ( .i ` W ) x ) = ( 0g ` (Scalar ` W ) ) )
59	32, 58	sylan 488	. . . . . . 7 |- ( ( ( ( W e. PreHil /\ S C_ V ) /\ ( r e. ( Base ` (Scalar ` W ) ) /\ y e. ( ._|_ ` S ) /\ z e. ( ._|_ ` S ) ) ) /\ x e. S ) -> ( z ( .i ` W ) x ) = ( 0g ` (Scalar ` W ) ) )
60	57, 59	oveq12d 6668	. . . . . 6 |- ( ( ( ( W e. PreHil /\ S C_ V ) /\ ( r e. ( Base ` (Scalar ` W ) ) /\ y e. ( ._|_ ` S ) /\ z e. ( ._|_ ` S ) ) ) /\ x e. S ) -> ( ( ( r ( .s ` W ) y ) ( .i ` W ) x ) ( +g ` (Scalar ` W ) ) ( z ( .i ` W ) x ) ) = ( ( 0g ` (Scalar ` W ) ) ( +g ` (Scalar ` W ) ) ( 0g ` (Scalar ` W ) ) ) )
61	13	lmodfgrp 18872	. . . . . . 7 |- ( W e. LMod -> (Scalar ` W ) e. Grp )
62	29, 15	grpidcl 17450	. . . . . . . 8 |- ( (Scalar ` W ) e. Grp -> ( 0g ` (Scalar ` W ) ) e. ( Base ` (Scalar ` W ) ) )
63	29, 41, 15	grplid 17452	. . . . . . . 8 |- ( ( (Scalar ` W ) e. Grp /\ ( 0g ` (Scalar ` W ) ) e. ( Base ` (Scalar ` W ) ) ) -> ( ( 0g ` (Scalar ` W ) ) ( +g ` (Scalar ` W ) ) ( 0g ` (Scalar ` W ) ) ) = ( 0g ` (Scalar ` W ) ) )
64	62, 63	mpdan 702	. . . . . . 7 |- ( (Scalar ` W ) e. Grp -> ( ( 0g ` (Scalar ` W ) ) ( +g ` (Scalar ` W ) ) ( 0g ` (Scalar ` W ) ) ) = ( 0g ` (Scalar ` W ) ) )
65	52, 61, 64	3syl 18	. . . . . 6 |- ( ( ( ( W e. PreHil /\ S C_ V ) /\ ( r e. ( Base ` (Scalar ` W ) ) /\ y e. ( ._|_ ` S ) /\ z e. ( ._|_ ` S ) ) ) /\ x e. S ) -> ( ( 0g ` (Scalar ` W ) ) ( +g ` (Scalar ` W ) ) ( 0g ` (Scalar ` W ) ) ) = ( 0g ` (Scalar ` W ) ) )
66	43, 60, 65	3eqtrd 2660	. . . . 5 |- ( ( ( ( W e. PreHil /\ S C_ V ) /\ ( r e. ( Base ` (Scalar ` W ) ) /\ y e. ( ._|_ ` S ) /\ z e. ( ._|_ ` S ) ) ) /\ x e. S ) -> ( ( ( r ( .s ` W ) y ) ( +g ` W ) z ) ( .i ` W ) x ) = ( 0g ` (Scalar ` W ) ) )
67	66	ralrimiva 2966	. . . 4 |- ( ( ( W e. PreHil /\ S C_ V ) /\ ( r e. ( Base ` (Scalar ` W ) ) /\ y e. ( ._|_ ` S ) /\ z e. ( ._|_ ` S ) ) ) -> A. x e. S ( ( ( r ( .s ` W ) y ) ( +g ` W ) z ) ( .i ` W ) x ) = ( 0g ` (Scalar ` W ) ) )
68	1, 14, 13, 15, 2	elocv 20012	. . . 4 |- ( ( ( r ( .s ` W ) y ) ( +g ` W ) z ) e. ( ._|_ ` S ) <-> ( S C_ V /\ ( ( r ( .s ` W ) y ) ( +g ` W ) z ) e. V /\ A. x e. S ( ( ( r ( .s ` W ) y ) ( +g ` W ) z ) ( .i ` W ) x ) = ( 0g ` (Scalar ` W ) ) ) )
69	23, 36, 67, 68	syl3anbrc 1246	. . 3 |- ( ( ( W e. PreHil /\ S C_ V ) /\ ( r e. ( Base ` (Scalar ` W ) ) /\ y e. ( ._|_ ` S ) /\ z e. ( ._|_ ` S ) ) ) -> ( ( r ( .s ` W ) y ) ( +g ` W ) z ) e. ( ._|_ ` S ) )
70	69	ralrimivvva 2972	. 2 |- ( ( W e. PreHil /\ S C_ V ) -> A. r e. ( Base ` (Scalar ` W ) ) A. y e. ( ._|_ ` S ) A. z e. ( ._|_ ` S ) ( ( r ( .s ` W ) y ) ( +g ` W ) z ) e. ( ._|_ ` S ) )
71		ocvlss.l	. . 3 |- L = ( LSubSp ` W )
72	13, 29, 1, 34, 28, 71	islss 18935	. 2 |- ( ( ._|_ ` S ) e. L <-> ( ( ._|_ ` S ) C_ V /\ ( ._|_ ` S ) =/= (/) /\ A. r e. ( Base ` (Scalar ` W ) ) A. y e. ( ._|_ ` S ) A. z e. ( ._|_ ` S ) ( ( r ( .s ` W ) y ) ( +g ` W ) z ) e. ( ._|_ ` S ) ) )
73	4, 22, 70, 72	syl3anbrc 1246	1 |- ( ( W e. PreHil /\ S C_ V ) -> ( ._|_ ` S ) e. L )

Syntax hints:   -> wi 4   /\ wa 384   /\ w3a 1037   = wceq 1483   e. wcel 1990   =/= wne 2794   A.wral 2912   C_ wss 3574   (/)c0 3915   ` cfv 5888  (class class class)co 6650   Basecbs 15857   +g cplusg 15941   .rcmulr 15942  Scalarcsca 15944   .scvsca 15945   .icip 15946   0gc0g 16100   Grpcgrp 17422   Ringcrg 18547   LModclmod 18863   LSubSpclss 18932   PreHilcphl 19969   ocvcocv 20004

This theorem was proved from axioms:  ax-mp 5  ax-1 6  ax-2 7  ax-3 8  ax-gen 1722  ax-4 1737  ax-5 1839  ax-6 1888  ax-7 1935  ax-8 1992  ax-9 1999  ax-10 2019  ax-11 2034  ax-12 2047  ax-13 2246  ax-ext 2602  ax-rep 4771  ax-sep 4781  ax-nul 4789  ax-pow 4843  ax-pr 4906  ax-un 6949  ax-cnex 9992  ax-resscn 9993  ax-1cn 9994  ax-icn 9995  ax-addcl 9996  ax-addrcl 9997  ax-mulcl 9998  ax-mulrcl 9999  ax-mulcom 10000  ax-addass 10001  ax-mulass 10002  ax-distr 10003  ax-i2m1 10004  ax-1ne0 10005  ax-1rid 10006  ax-rnegex 10007  ax-rrecex 10008  ax-cnre 10009  ax-pre-lttri 10010  ax-pre-lttrn 10011  ax-pre-ltadd 10012  ax-pre-mulgt0 10013

This theorem depends on definitions:  df-bi 197  df-or 385  df-an 386  df-3or 1038  df-3an 1039  df-tru 1486  df-ex 1705  df-nf 1710  df-sb 1881  df-eu 2474  df-mo 2475  df-clab 2609  df-cleq 2615  df-clel 2618  df-nfc 2753  df-ne 2795  df-nel 2898  df-ral 2917  df-rex 2918  df-reu 2919  df-rmo 2920  df-rab 2921  df-v 3202  df-sbc 3436  df-csb 3534  df-dif 3577  df-un 3579  df-in 3581  df-ss 3588  df-pss 3590  df-nul 3916  df-if 4087  df-pw 4160  df-sn 4178  df-pr 4180  df-tp 4182  df-op 4184  df-uni 4437  df-iun 4522  df-br 4654  df-opab 4713  df-mpt 4730  df-tr 4753  df-id 5024  df-eprel 5029  df-po 5035  df-so 5036  df-fr 5073  df-we 5075  df-xp 5120  df-rel 5121  df-cnv 5122  df-co 5123  df-dm 5124  df-rn 5125  df-res 5126  df-ima 5127  df-pred 5680  df-ord 5726  df-on 5727  df-lim 5728  df-suc 5729  df-iota 5851  df-fun 5890  df-fn 5891  df-f 5892  df-f1 5893  df-fo 5894  df-f1o 5895  df-fv 5896  df-riota 6611  df-ov 6653  df-oprab 6654  df-mpt2 6655  df-om 7066  df-wrecs 7407  df-recs 7468  df-rdg 7506  df-er 7742  df-en 7956  df-dom 7957  df-sdom 7958  df-pnf 10076  df-mnf 10077  df-xr 10078  df-ltxr 10079  df-le 10080  df-sub 10268  df-neg 10269  df-nn 11021  df-2 11079  df-3 11080  df-4 11081  df-5 11082  df-6 11083  df-7 11084  df-8 11085  df-ndx 15860  df-slot 15861  df-base 15863  df-sets 15864  df-plusg 15954  df-sca 15957  df-vsca 15958  df-ip 15959  df-0g 16102  df-mgm 17242  df-sgrp 17284  df-mnd 17295  df-grp 17425  df-ghm 17658  df-mgp 18490  df-ring 18549  df-lmod 18865  df-lss 18933  df-lmhm 19022  df-lvec 19103  df-sra 19172  df-rgmod 19173  df-phl 19971  df-ocv 20007

This theorem is referenced by:  ocvin  20018  ocvlsp  20020  csslss  20035  pjdm2  20055  pjff  20056  pjf2  20058  pjfo  20059  ocvpj  20061  pjthlem2  23209  pjth  23210