Theorem yonedalem3b 16919

Description: Lemma for yoneda 16923. (Contributed by Mario Carneiro, 29-Jan-2017.)

Hypotheses

Ref	Expression
yoneda.y	|- Y = (Yon ` C )
yoneda.b	|- B = ( Base ` C )
yoneda.1	|- .1. = ( Id ` C )
yoneda.o	|- O = (oppCat ` C )
yoneda.s	|- S = ( SetCat ` U )
yoneda.t	|- T = ( SetCat ` V )
yoneda.q	|- Q = ( O FuncCat S )
yoneda.h	|- H = (HomF ` Q )
yoneda.r	|- R = ( ( Q X.c O ) FuncCat T )
yoneda.e	|- E = ( O evalF S )
yoneda.z	|- Z = ( H o.func ( ( <. ( 1st ` Y ) , tpos ( 2nd ` Y ) >. o.func ( Q 2ndF O ) ) ⟨,⟩F ( Q 1stF O ) ) )
yoneda.c	|- ( ph -> C e. Cat )
yoneda.w	|- ( ph -> V e. W )
yoneda.u	|- ( ph -> ran ( Hom f ` C ) C_ U )
yoneda.v	|- ( ph -> ( ran ( Hom f ` Q ) u. U ) C_ V )
yonedalem21.f	|- ( ph -> F e. ( O Func S ) )
yonedalem21.x	|- ( ph -> X e. B )
yonedalem22.g	|- ( ph -> G e. ( O Func S ) )
yonedalem22.p	|- ( ph -> P e. B )
yonedalem22.a	|- ( ph -> A e. ( F ( O Nat S ) G ) )
yonedalem22.k	|- ( ph -> K e. ( P ( Hom ` C ) X ) )
yonedalem3.m	|- M = ( f e. ( O Func S ) , x e. B |-> ( a e. ( ( ( 1st ` Y ) ` x ) ( O Nat S ) f ) |-> ( ( a ` x ) ` ( .1. ` x ) ) ) )

Assertion

Ref	Expression
yonedalem3b	|- ( ph -> ( ( G M P ) ( <. ( F ( 1st ` Z ) X ) , ( G ( 1st ` Z ) P ) >. (comp ` T ) ( G ( 1st ` E ) P ) ) ( A ( <. F , X >. ( 2nd ` Z ) <. G , P >. ) K ) ) = ( ( A ( <. F , X >. ( 2nd ` E ) <. G , P >. ) K ) ( <. ( F ( 1st ` Z ) X ) , ( F ( 1st ` E ) X ) >. (comp ` T ) ( G ( 1st ` E ) P ) ) ( F M X ) ) )

Distinct variable groups:   f, a, x, .1.   A, a   C, a, f, x   E, a, f   F, a, f, x   K, a   B, a, f, x   G, a, f, x   O, a, f, x   S, a, f, x   Q, a, f, x   T, f   P, a, f, x   ph, a, f, x   Y, a, f, x   Z, a, f, x   X, a, f, x

Allowed substitution hints:   A( x, f)   R( x, f, a)   T( x, a)   U( x, f, a)   E( x)   H( x, f, a)   K( x, f)   M( x, f, a)   V( x, f, a)   W( x, f, a)

Proof of Theorem yonedalem3b

Dummy variables b y are mutually distinct and distinct from all other variables.

Step	Hyp	Ref	Expression
1		oveq2 6658	. . . . . . . 8 |- ( b = a -> ( A ( <. ( ( 1st ` Y ) ` X ) , F >. (comp ` Q ) G ) b ) = ( A ( <. ( ( 1st ` Y ) ` X ) , F >. (comp ` Q ) G ) a ) )
2	1	oveq1d 6665	. . . . . . 7 |- ( b = a -> ( ( A ( <. ( ( 1st ` Y ) ` X ) , F >. (comp ` Q ) G ) b ) ( <. ( ( 1st ` Y ) ` P ) , ( ( 1st ` Y ) ` X ) >. (comp ` Q ) G ) ( ( P ( 2nd ` Y ) X ) ` K ) ) = ( ( A ( <. ( ( 1st ` Y ) ` X ) , F >. (comp ` Q ) G ) a ) ( <. ( ( 1st ` Y ) ` P ) , ( ( 1st ` Y ) ` X ) >. (comp ` Q ) G ) ( ( P ( 2nd ` Y ) X ) ` K ) ) )
3	2	fveq1d 6193	. . . . . 6 |- ( b = a -> ( ( ( A ( <. ( ( 1st ` Y ) ` X ) , F >. (comp ` Q ) G ) b ) ( <. ( ( 1st ` Y ) ` P ) , ( ( 1st ` Y ) ` X ) >. (comp ` Q ) G ) ( ( P ( 2nd ` Y ) X ) ` K ) ) ` P ) = ( ( ( A ( <. ( ( 1st ` Y ) ` X ) , F >. (comp ` Q ) G ) a ) ( <. ( ( 1st ` Y ) ` P ) , ( ( 1st ` Y ) ` X ) >. (comp ` Q ) G ) ( ( P ( 2nd ` Y ) X ) ` K ) ) ` P ) )
4	3	fveq1d 6193	. . . . 5 |- ( b = a -> ( ( ( ( A ( <. ( ( 1st ` Y ) ` X ) , F >. (comp ` Q ) G ) b ) ( <. ( ( 1st ` Y ) ` P ) , ( ( 1st ` Y ) ` X ) >. (comp ` Q ) G ) ( ( P ( 2nd ` Y ) X ) ` K ) ) ` P ) ` ( .1. ` P ) ) = ( ( ( ( A ( <. ( ( 1st ` Y ) ` X ) , F >. (comp ` Q ) G ) a ) ( <. ( ( 1st ` Y ) ` P ) , ( ( 1st ` Y ) ` X ) >. (comp ` Q ) G ) ( ( P ( 2nd ` Y ) X ) ` K ) ) ` P ) ` ( .1. ` P ) ) )
5	4	cbvmptv 4750	. . . 4 |- ( b e. ( ( ( 1st ` Y ) ` X ) ( O Nat S ) F ) |-> ( ( ( ( A ( <. ( ( 1st ` Y ) ` X ) , F >. (comp ` Q ) G ) b ) ( <. ( ( 1st ` Y ) ` P ) , ( ( 1st ` Y ) ` X ) >. (comp ` Q ) G ) ( ( P ( 2nd ` Y ) X ) ` K ) ) ` P ) ` ( .1. ` P ) ) ) = ( a e. ( ( ( 1st ` Y ) ` X ) ( O Nat S ) F ) |-> ( ( ( ( A ( <. ( ( 1st ` Y ) ` X ) , F >. (comp ` Q ) G ) a ) ( <. ( ( 1st ` Y ) ` P ) , ( ( 1st ` Y ) ` X ) >. (comp ` Q ) G ) ( ( P ( 2nd ` Y ) X ) ` K ) ) ` P ) ` ( .1. ` P ) ) )
6		yoneda.q	. . . . . . . . 9 |- Q = ( O FuncCat S )
7		eqid 2622	. . . . . . . . 9 |- ( O Nat S ) = ( O Nat S )
8		yoneda.o	. . . . . . . . . 10 |- O = (oppCat ` C )
9		yoneda.b	. . . . . . . . . 10 |- B = ( Base ` C )
10	8, 9	oppcbas 16378	. . . . . . . . 9 |- B = ( Base ` O )
11		eqid 2622	. . . . . . . . 9 |- (comp ` S ) = (comp ` S )
12		eqid 2622	. . . . . . . . 9 |- (comp ` Q ) = (comp ` Q )
13		eqid 2622	. . . . . . . . . . . 12 |- ( Hom ` C ) = ( Hom ` C )
14	6, 7	fuchom 16621	. . . . . . . . . . . 12 |- ( O Nat S ) = ( Hom ` Q )
15		relfunc 16522	. . . . . . . . . . . . 13 |- Rel ( C Func Q )
16		yoneda.y	. . . . . . . . . . . . . 14 |- Y = (Yon ` C )
17		yoneda.c	. . . . . . . . . . . . . 14 |- ( ph -> C e. Cat )
18		yoneda.s	. . . . . . . . . . . . . 14 |- S = ( SetCat ` U )
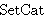19		yoneda.w	. . . . . . . . . . . . . . 15 |- ( ph -> V e. W )
20		yoneda.v	. . . . . . . . . . . . . . . 16 |- ( ph -> ( ran ( Hom f ` Q ) u. U ) C_ V )
21	20	unssbd 3791	. . . . . . . . . . . . . . 15 |- ( ph -> U C_ V )
22	19, 21	ssexd 4805	. . . . . . . . . . . . . 14 |- ( ph -> U e. _V )
23		yoneda.u	. . . . . . . . . . . . . 14 |- ( ph -> ran ( Hom f ` C ) C_ U )
24	16, 17, 8, 18, 6, 22, 23	yoncl 16902	. . . . . . . . . . . . 13 |- ( ph -> Y e. ( C Func Q ) )
25		1st2ndbr 7217	. . . . . . . . . . . . 13 |- ( ( Rel ( C Func Q ) /\ Y e. ( C Func Q ) ) -> ( 1st ` Y ) ( C Func Q ) ( 2nd ` Y ) )
26	15, 24, 25	sylancr 695	. . . . . . . . . . . 12 |- ( ph -> ( 1st ` Y ) ( C Func Q ) ( 2nd ` Y ) )
27		yonedalem22.p	. . . . . . . . . . . 12 |- ( ph -> P e. B )
28		yonedalem21.x	. . . . . . . . . . . 12 |- ( ph -> X e. B )
29	9, 13, 14, 26, 27, 28	funcf2 16528	. . . . . . . . . . 11 |- ( ph -> ( P ( 2nd ` Y ) X ) : ( P ( Hom ` C ) X ) --> ( ( ( 1st ` Y ) ` P ) ( O Nat S ) ( ( 1st ` Y ) ` X ) ) )
30		yonedalem22.k	. . . . . . . . . . 11 |- ( ph -> K e. ( P ( Hom ` C ) X ) )
31	29, 30	ffvelrnd 6360	. . . . . . . . . 10 |- ( ph -> ( ( P ( 2nd ` Y ) X ) ` K ) e. ( ( ( 1st ` Y ) ` P ) ( O Nat S ) ( ( 1st ` Y ) ` X ) ) )
32	31	adantr 481	. . . . . . . . 9 |- ( ( ph /\ a e. ( ( ( 1st ` Y ) ` X ) ( O Nat S ) F ) ) -> ( ( P ( 2nd ` Y ) X ) ` K ) e. ( ( ( 1st ` Y ) ` P ) ( O Nat S ) ( ( 1st ` Y ) ` X ) ) )
33		simpr 477	. . . . . . . . . 10 |- ( ( ph /\ a e. ( ( ( 1st ` Y ) ` X ) ( O Nat S ) F ) ) -> a e. ( ( ( 1st ` Y ) ` X ) ( O Nat S ) F ) )
34		yonedalem22.a	. . . . . . . . . . 11 |- ( ph -> A e. ( F ( O Nat S ) G ) )
35	34	adantr 481	. . . . . . . . . 10 |- ( ( ph /\ a e. ( ( ( 1st ` Y ) ` X ) ( O Nat S ) F ) ) -> A e. ( F ( O Nat S ) G ) )
36	6, 7, 12, 33, 35	fuccocl 16624	. . . . . . . . 9 |- ( ( ph /\ a e. ( ( ( 1st ` Y ) ` X ) ( O Nat S ) F ) ) -> ( A ( <. ( ( 1st ` Y ) ` X ) , F >. (comp ` Q ) G ) a ) e. ( ( ( 1st ` Y ) ` X ) ( O Nat S ) G ) )
37	27	adantr 481	. . . . . . . . 9 |- ( ( ph /\ a e. ( ( ( 1st ` Y ) ` X ) ( O Nat S ) F ) ) -> P e. B )
38	6, 7, 10, 11, 12, 32, 36, 37	fuccoval 16623	. . . . . . . 8 |- ( ( ph /\ a e. ( ( ( 1st ` Y ) ` X ) ( O Nat S ) F ) ) -> ( ( ( A ( <. ( ( 1st ` Y ) ` X ) , F >. (comp ` Q ) G ) a ) ( <. ( ( 1st ` Y ) ` P ) , ( ( 1st ` Y ) ` X ) >. (comp ` Q ) G ) ( ( P ( 2nd ` Y ) X ) ` K ) ) ` P ) = ( ( ( A ( <. ( ( 1st ` Y ) ` X ) , F >. (comp ` Q ) G ) a ) ` P ) ( <. ( ( 1st ` ( ( 1st ` Y ) ` P ) ) ` P ) , ( ( 1st ` ( ( 1st ` Y ) ` X ) ) ` P ) >. (comp ` S ) ( ( 1st ` G ) ` P ) ) ( ( ( P ( 2nd ` Y ) X ) ` K ) ` P ) ) )
39	6, 7, 10, 11, 12, 33, 35, 37	fuccoval 16623	. . . . . . . . . 10 |- ( ( ph /\ a e. ( ( ( 1st ` Y ) ` X ) ( O Nat S ) F ) ) -> ( ( A ( <. ( ( 1st ` Y ) ` X ) , F >. (comp ` Q ) G ) a ) ` P ) = ( ( A ` P ) ( <. ( ( 1st ` ( ( 1st ` Y ) ` X ) ) ` P ) , ( ( 1st ` F ) ` P ) >. (comp ` S ) ( ( 1st ` G ) ` P ) ) ( a ` P ) ) )
40	22	adantr 481	. . . . . . . . . . 11 |- ( ( ph /\ a e. ( ( ( 1st ` Y ) ` X ) ( O Nat S ) F ) ) -> U e. _V )
41		eqid 2622	. . . . . . . . . . . . . . 15 |- ( Base ` S ) = ( Base ` S )
42		relfunc 16522	. . . . . . . . . . . . . . . 16 |- Rel ( O Func S )
43	6	fucbas 16620	. . . . . . . . . . . . . . . . . 18 |- ( O Func S ) = ( Base ` Q )
44	9, 43, 26	funcf1 16526	. . . . . . . . . . . . . . . . 17 |- ( ph -> ( 1st ` Y ) : B --> ( O Func S ) )
45	44, 28	ffvelrnd 6360	. . . . . . . . . . . . . . . 16 |- ( ph -> ( ( 1st ` Y ) ` X ) e. ( O Func S ) )
46		1st2ndbr 7217	. . . . . . . . . . . . . . . 16 |- ( ( Rel ( O Func S ) /\ ( ( 1st ` Y ) ` X ) e. ( O Func S ) ) -> ( 1st ` ( ( 1st ` Y ) ` X ) ) ( O Func S ) ( 2nd ` ( ( 1st ` Y ) ` X ) ) )
47	42, 45, 46	sylancr 695	. . . . . . . . . . . . . . 15 |- ( ph -> ( 1st ` ( ( 1st ` Y ) ` X ) ) ( O Func S ) ( 2nd ` ( ( 1st ` Y ) ` X ) ) )
48	10, 41, 47	funcf1 16526	. . . . . . . . . . . . . 14 |- ( ph -> ( 1st ` ( ( 1st ` Y ) ` X ) ) : B --> ( Base ` S ) )
49	18, 22	setcbas 16728	. . . . . . . . . . . . . . 15 |- ( ph -> U = ( Base ` S ) )
50	49	feq3d 6032	. . . . . . . . . . . . . 14 |- ( ph -> ( ( 1st ` ( ( 1st ` Y ) ` X ) ) : B --> U <-> ( 1st ` ( ( 1st ` Y ) ` X ) ) : B --> ( Base ` S ) ) )
51	48, 50	mpbird 247	. . . . . . . . . . . . 13 |- ( ph -> ( 1st ` ( ( 1st ` Y ) ` X ) ) : B --> U )
52	51, 27	ffvelrnd 6360	. . . . . . . . . . . 12 |- ( ph -> ( ( 1st ` ( ( 1st ` Y ) ` X ) ) ` P ) e. U )
53	52	adantr 481	. . . . . . . . . . 11 |- ( ( ph /\ a e. ( ( ( 1st ` Y ) ` X ) ( O Nat S ) F ) ) -> ( ( 1st ` ( ( 1st ` Y ) ` X ) ) ` P ) e. U )
54		yonedalem21.f	. . . . . . . . . . . . . . . 16 |- ( ph -> F e. ( O Func S ) )
55		1st2ndbr 7217	. . . . . . . . . . . . . . . 16 |- ( ( Rel ( O Func S ) /\ F e. ( O Func S ) ) -> ( 1st ` F ) ( O Func S ) ( 2nd ` F ) )
56	42, 54, 55	sylancr 695	. . . . . . . . . . . . . . 15 |- ( ph -> ( 1st ` F ) ( O Func S ) ( 2nd ` F ) )
57	10, 41, 56	funcf1 16526	. . . . . . . . . . . . . 14 |- ( ph -> ( 1st ` F ) : B --> ( Base ` S ) )
58	49	feq3d 6032	. . . . . . . . . . . . . 14 |- ( ph -> ( ( 1st ` F ) : B --> U <-> ( 1st ` F ) : B --> ( Base ` S ) ) )
59	57, 58	mpbird 247	. . . . . . . . . . . . 13 |- ( ph -> ( 1st ` F ) : B --> U )
60	59, 27	ffvelrnd 6360	. . . . . . . . . . . 12 |- ( ph -> ( ( 1st ` F ) ` P ) e. U )
61	60	adantr 481	. . . . . . . . . . 11 |- ( ( ph /\ a e. ( ( ( 1st ` Y ) ` X ) ( O Nat S ) F ) ) -> ( ( 1st ` F ) ` P ) e. U )
62		yonedalem22.g	. . . . . . . . . . . . . . . 16 |- ( ph -> G e. ( O Func S ) )
63		1st2ndbr 7217	. . . . . . . . . . . . . . . 16 |- ( ( Rel ( O Func S ) /\ G e. ( O Func S ) ) -> ( 1st ` G ) ( O Func S ) ( 2nd ` G ) )
64	42, 62, 63	sylancr 695	. . . . . . . . . . . . . . 15 |- ( ph -> ( 1st ` G ) ( O Func S ) ( 2nd ` G ) )
65	10, 41, 64	funcf1 16526	. . . . . . . . . . . . . 14 |- ( ph -> ( 1st ` G ) : B --> ( Base ` S ) )
66	65, 27	ffvelrnd 6360	. . . . . . . . . . . . 13 |- ( ph -> ( ( 1st ` G ) ` P ) e. ( Base ` S ) )
67	66, 49	eleqtrrd 2704	. . . . . . . . . . . 12 |- ( ph -> ( ( 1st ` G ) ` P ) e. U )
68	67	adantr 481	. . . . . . . . . . 11 |- ( ( ph /\ a e. ( ( ( 1st ` Y ) ` X ) ( O Nat S ) F ) ) -> ( ( 1st ` G ) ` P ) e. U )
69	7, 33	nat1st2nd 16611	. . . . . . . . . . . . 13 |- ( ( ph /\ a e. ( ( ( 1st ` Y ) ` X ) ( O Nat S ) F ) ) -> a e. ( <. ( 1st ` ( ( 1st ` Y ) ` X ) ) , ( 2nd ` ( ( 1st ` Y ) ` X ) ) >. ( O Nat S ) <. ( 1st ` F ) , ( 2nd ` F ) >. ) )
70		eqid 2622	. . . . . . . . . . . . 13 |- ( Hom ` S ) = ( Hom ` S )
71	7, 69, 10, 70, 37	natcl 16613	. . . . . . . . . . . 12 |- ( ( ph /\ a e. ( ( ( 1st ` Y ) ` X ) ( O Nat S ) F ) ) -> ( a ` P ) e. ( ( ( 1st ` ( ( 1st ` Y ) ` X ) ) ` P ) ( Hom ` S ) ( ( 1st ` F ) ` P ) ) )
72	18, 40, 70, 53, 61	elsetchom 16731	. . . . . . . . . . . 12 |- ( ( ph /\ a e. ( ( ( 1st ` Y ) ` X ) ( O Nat S ) F ) ) -> ( ( a ` P ) e. ( ( ( 1st ` ( ( 1st ` Y ) ` X ) ) ` P ) ( Hom ` S ) ( ( 1st ` F ) ` P ) ) <-> ( a ` P ) : ( ( 1st ` ( ( 1st ` Y ) ` X ) ) ` P ) --> ( ( 1st ` F ) ` P ) ) )
73	71, 72	mpbid 222	. . . . . . . . . . 11 |- ( ( ph /\ a e. ( ( ( 1st ` Y ) ` X ) ( O Nat S ) F ) ) -> ( a ` P ) : ( ( 1st ` ( ( 1st ` Y ) ` X ) ) ` P ) --> ( ( 1st ` F ) ` P ) )
74	7, 34	nat1st2nd 16611	. . . . . . . . . . . . . 14 |- ( ph -> A e. ( <. ( 1st ` F ) , ( 2nd ` F ) >. ( O Nat S ) <. ( 1st ` G ) , ( 2nd ` G ) >. ) )
75	7, 74, 10, 70, 27	natcl 16613	. . . . . . . . . . . . 13 |- ( ph -> ( A ` P ) e. ( ( ( 1st ` F ) ` P ) ( Hom ` S ) ( ( 1st ` G ) ` P ) ) )
76	18, 22, 70, 60, 67	elsetchom 16731	. . . . . . . . . . . . 13 |- ( ph -> ( ( A ` P ) e. ( ( ( 1st ` F ) ` P ) ( Hom ` S ) ( ( 1st ` G ) ` P ) ) <-> ( A ` P ) : ( ( 1st ` F ) ` P ) --> ( ( 1st ` G ) ` P ) ) )
77	75, 76	mpbid 222	. . . . . . . . . . . 12 |- ( ph -> ( A ` P ) : ( ( 1st ` F ) ` P ) --> ( ( 1st ` G ) ` P ) )
78	77	adantr 481	. . . . . . . . . . 11 |- ( ( ph /\ a e. ( ( ( 1st ` Y ) ` X ) ( O Nat S ) F ) ) -> ( A ` P ) : ( ( 1st ` F ) ` P ) --> ( ( 1st ` G ) ` P ) )
79	18, 40, 11, 53, 61, 68, 73, 78	setcco 16733	. . . . . . . . . 10 |- ( ( ph /\ a e. ( ( ( 1st ` Y ) ` X ) ( O Nat S ) F ) ) -> ( ( A ` P ) ( <. ( ( 1st ` ( ( 1st ` Y ) ` X ) ) ` P ) , ( ( 1st ` F ) ` P ) >. (comp ` S ) ( ( 1st ` G ) ` P ) ) ( a ` P ) ) = ( ( A ` P ) o. ( a ` P ) ) )
80	39, 79	eqtrd 2656	. . . . . . . . 9 |- ( ( ph /\ a e. ( ( ( 1st ` Y ) ` X ) ( O Nat S ) F ) ) -> ( ( A ( <. ( ( 1st ` Y ) ` X ) , F >. (comp ` Q ) G ) a ) ` P ) = ( ( A ` P ) o. ( a ` P ) ) )
81	80	oveq1d 6665	. . . . . . . 8 |- ( ( ph /\ a e. ( ( ( 1st ` Y ) ` X ) ( O Nat S ) F ) ) -> ( ( ( A ( <. ( ( 1st ` Y ) ` X ) , F >. (comp ` Q ) G ) a ) ` P ) ( <. ( ( 1st ` ( ( 1st ` Y ) ` P ) ) ` P ) , ( ( 1st ` ( ( 1st ` Y ) ` X ) ) ` P ) >. (comp ` S ) ( ( 1st ` G ) ` P ) ) ( ( ( P ( 2nd ` Y ) X ) ` K ) ` P ) ) = ( ( ( A ` P ) o. ( a ` P ) ) ( <. ( ( 1st ` ( ( 1st ` Y ) ` P ) ) ` P ) , ( ( 1st ` ( ( 1st ` Y ) ` X ) ) ` P ) >. (comp ` S ) ( ( 1st ` G ) ` P ) ) ( ( ( P ( 2nd ` Y ) X ) ` K ) ` P ) ) )
82	44, 27	ffvelrnd 6360	. . . . . . . . . . . . . 14 |- ( ph -> ( ( 1st ` Y ) ` P ) e. ( O Func S ) )
83		1st2ndbr 7217	. . . . . . . . . . . . . 14 |- ( ( Rel ( O Func S ) /\ ( ( 1st ` Y ) ` P ) e. ( O Func S ) ) -> ( 1st ` ( ( 1st ` Y ) ` P ) ) ( O Func S ) ( 2nd ` ( ( 1st ` Y ) ` P ) ) )
84	42, 82, 83	sylancr 695	. . . . . . . . . . . . 13 |- ( ph -> ( 1st ` ( ( 1st ` Y ) ` P ) ) ( O Func S ) ( 2nd ` ( ( 1st ` Y ) ` P ) ) )
85	10, 41, 84	funcf1 16526	. . . . . . . . . . . 12 |- ( ph -> ( 1st ` ( ( 1st ` Y ) ` P ) ) : B --> ( Base ` S ) )
86	85, 27	ffvelrnd 6360	. . . . . . . . . . 11 |- ( ph -> ( ( 1st ` ( ( 1st ` Y ) ` P ) ) ` P ) e. ( Base ` S ) )
87	86, 49	eleqtrrd 2704	. . . . . . . . . 10 |- ( ph -> ( ( 1st ` ( ( 1st ` Y ) ` P ) ) ` P ) e. U )
88	87	adantr 481	. . . . . . . . 9 |- ( ( ph /\ a e. ( ( ( 1st ` Y ) ` X ) ( O Nat S ) F ) ) -> ( ( 1st ` ( ( 1st ` Y ) ` P ) ) ` P ) e. U )
89	7, 31	nat1st2nd 16611	. . . . . . . . . . . 12 |- ( ph -> ( ( P ( 2nd ` Y ) X ) ` K ) e. ( <. ( 1st ` ( ( 1st ` Y ) ` P ) ) , ( 2nd ` ( ( 1st ` Y ) ` P ) ) >. ( O Nat S ) <. ( 1st ` ( ( 1st ` Y ) ` X ) ) , ( 2nd ` ( ( 1st ` Y ) ` X ) ) >. ) )
90	7, 89, 10, 70, 27	natcl 16613	. . . . . . . . . . 11 |- ( ph -> ( ( ( P ( 2nd ` Y ) X ) ` K ) ` P ) e. ( ( ( 1st ` ( ( 1st ` Y ) ` P ) ) ` P ) ( Hom ` S ) ( ( 1st ` ( ( 1st ` Y ) ` X ) ) ` P ) ) )
91	18, 22, 70, 87, 52	elsetchom 16731	. . . . . . . . . . 11 |- ( ph -> ( ( ( ( P ( 2nd ` Y ) X ) ` K ) ` P ) e. ( ( ( 1st ` ( ( 1st ` Y ) ` P ) ) ` P ) ( Hom ` S ) ( ( 1st ` ( ( 1st ` Y ) ` X ) ) ` P ) ) <-> ( ( ( P ( 2nd ` Y ) X ) ` K ) ` P ) : ( ( 1st ` ( ( 1st ` Y ) ` P ) ) ` P ) --> ( ( 1st ` ( ( 1st ` Y ) ` X ) ) ` P ) ) )
92	90, 91	mpbid 222	. . . . . . . . . 10 |- ( ph -> ( ( ( P ( 2nd ` Y ) X ) ` K ) ` P ) : ( ( 1st ` ( ( 1st ` Y ) ` P ) ) ` P ) --> ( ( 1st ` ( ( 1st ` Y ) ` X ) ) ` P ) )
93	92	adantr 481	. . . . . . . . 9 |- ( ( ph /\ a e. ( ( ( 1st ` Y ) ` X ) ( O Nat S ) F ) ) -> ( ( ( P ( 2nd ` Y ) X ) ` K ) ` P ) : ( ( 1st ` ( ( 1st ` Y ) ` P ) ) ` P ) --> ( ( 1st ` ( ( 1st ` Y ) ` X ) ) ` P ) )
94		fco 6058	. . . . . . . . . 10 |- ( ( ( A ` P ) : ( ( 1st ` F ) ` P ) --> ( ( 1st ` G ) ` P ) /\ ( a ` P ) : ( ( 1st ` ( ( 1st ` Y ) ` X ) ) ` P ) --> ( ( 1st ` F ) ` P ) ) -> ( ( A ` P ) o. ( a ` P ) ) : ( ( 1st ` ( ( 1st ` Y ) ` X ) ) ` P ) --> ( ( 1st ` G ) ` P ) )
95	78, 73, 94	syl2anc 693	. . . . . . . . 9 |- ( ( ph /\ a e. ( ( ( 1st ` Y ) ` X ) ( O Nat S ) F ) ) -> ( ( A ` P ) o. ( a ` P ) ) : ( ( 1st ` ( ( 1st ` Y ) ` X ) ) ` P ) --> ( ( 1st ` G ) ` P ) )
96	18, 40, 11, 88, 53, 68, 93, 95	setcco 16733	. . . . . . . 8 |- ( ( ph /\ a e. ( ( ( 1st ` Y ) ` X ) ( O Nat S ) F ) ) -> ( ( ( A ` P ) o. ( a ` P ) ) ( <. ( ( 1st ` ( ( 1st ` Y ) ` P ) ) ` P ) , ( ( 1st ` ( ( 1st ` Y ) ` X ) ) ` P ) >. (comp ` S ) ( ( 1st ` G ) ` P ) ) ( ( ( P ( 2nd ` Y ) X ) ` K ) ` P ) ) = ( ( ( A ` P ) o. ( a ` P ) ) o. ( ( ( P ( 2nd ` Y ) X ) ` K ) ` P ) ) )
97	38, 81, 96	3eqtrd 2660	. . . . . . 7 |- ( ( ph /\ a e. ( ( ( 1st ` Y ) ` X ) ( O Nat S ) F ) ) -> ( ( ( A ( <. ( ( 1st ` Y ) ` X ) , F >. (comp ` Q ) G ) a ) ( <. ( ( 1st ` Y ) ` P ) , ( ( 1st ` Y ) ` X ) >. (comp ` Q ) G ) ( ( P ( 2nd ` Y ) X ) ` K ) ) ` P ) = ( ( ( A ` P ) o. ( a ` P ) ) o. ( ( ( P ( 2nd ` Y ) X ) ` K ) ` P ) ) )
98	97	fveq1d 6193	. . . . . 6 |- ( ( ph /\ a e. ( ( ( 1st ` Y ) ` X ) ( O Nat S ) F ) ) -> ( ( ( ( A ( <. ( ( 1st ` Y ) ` X ) , F >. (comp ` Q ) G ) a ) ( <. ( ( 1st ` Y ) ` P ) , ( ( 1st ` Y ) ` X ) >. (comp ` Q ) G ) ( ( P ( 2nd ` Y ) X ) ` K ) ) ` P ) ` ( .1. ` P ) ) = ( ( ( ( A ` P ) o. ( a ` P ) ) o. ( ( ( P ( 2nd ` Y ) X ) ` K ) ` P ) ) ` ( .1. ` P ) ) )
99		yoneda.1	. . . . . . . . . 10 |- .1. = ( Id ` C )
100	9, 13, 99, 17, 27	catidcl 16343	. . . . . . . . 9 |- ( ph -> ( .1. ` P ) e. ( P ( Hom ` C ) P ) )
101	16, 9, 17, 27, 13, 27	yon11 16904	. . . . . . . . 9 |- ( ph -> ( ( 1st ` ( ( 1st ` Y ) ` P ) ) ` P ) = ( P ( Hom ` C ) P ) )
102	100, 101	eleqtrrd 2704	. . . . . . . 8 |- ( ph -> ( .1. ` P ) e. ( ( 1st ` ( ( 1st ` Y ) ` P ) ) ` P ) )
103	102	adantr 481	. . . . . . 7 |- ( ( ph /\ a e. ( ( ( 1st ` Y ) ` X ) ( O Nat S ) F ) ) -> ( .1. ` P ) e. ( ( 1st ` ( ( 1st ` Y ) ` P ) ) ` P ) )
104		fvco3 6275	. . . . . . 7 |- ( ( ( ( ( P ( 2nd ` Y ) X ) ` K ) ` P ) : ( ( 1st ` ( ( 1st ` Y ) ` P ) ) ` P ) --> ( ( 1st ` ( ( 1st ` Y ) ` X ) ) ` P ) /\ ( .1. ` P ) e. ( ( 1st ` ( ( 1st ` Y ) ` P ) ) ` P ) ) -> ( ( ( ( A ` P ) o. ( a ` P ) ) o. ( ( ( P ( 2nd ` Y ) X ) ` K ) ` P ) ) ` ( .1. ` P ) ) = ( ( ( A ` P ) o. ( a ` P ) ) ` ( ( ( ( P ( 2nd ` Y ) X ) ` K ) ` P ) ` ( .1. ` P ) ) ) )
105	93, 103, 104	syl2anc 693	. . . . . 6 |- ( ( ph /\ a e. ( ( ( 1st ` Y ) ` X ) ( O Nat S ) F ) ) -> ( ( ( ( A ` P ) o. ( a ` P ) ) o. ( ( ( P ( 2nd ` Y ) X ) ` K ) ` P ) ) ` ( .1. ` P ) ) = ( ( ( A ` P ) o. ( a ` P ) ) ` ( ( ( ( P ( 2nd ` Y ) X ) ` K ) ` P ) ` ( .1. ` P ) ) ) )
106	93, 103	ffvelrnd 6360	. . . . . . . 8 |- ( ( ph /\ a e. ( ( ( 1st ` Y ) ` X ) ( O Nat S ) F ) ) -> ( ( ( ( P ( 2nd ` Y ) X ) ` K ) ` P ) ` ( .1. ` P ) ) e. ( ( 1st ` ( ( 1st ` Y ) ` X ) ) ` P ) )
107		fvco3 6275	. . . . . . . 8 |- ( ( ( a ` P ) : ( ( 1st ` ( ( 1st ` Y ) ` X ) ) ` P ) --> ( ( 1st ` F ) ` P ) /\ ( ( ( ( P ( 2nd ` Y ) X ) ` K ) ` P ) ` ( .1. ` P ) ) e. ( ( 1st ` ( ( 1st ` Y ) ` X ) ) ` P ) ) -> ( ( ( A ` P ) o. ( a ` P ) ) ` ( ( ( ( P ( 2nd ` Y ) X ) ` K ) ` P ) ` ( .1. ` P ) ) ) = ( ( A ` P ) ` ( ( a ` P ) ` ( ( ( ( P ( 2nd ` Y ) X ) ` K ) ` P ) ` ( .1. ` P ) ) ) ) )
108	73, 106, 107	syl2anc 693	. . . . . . 7 |- ( ( ph /\ a e. ( ( ( 1st ` Y ) ` X ) ( O Nat S ) F ) ) -> ( ( ( A ` P ) o. ( a ` P ) ) ` ( ( ( ( P ( 2nd ` Y ) X ) ` K ) ` P ) ` ( .1. ` P ) ) ) = ( ( A ` P ) ` ( ( a ` P ) ` ( ( ( ( P ( 2nd ` Y ) X ) ` K ) ` P ) ` ( .1. ` P ) ) ) ) )
109	17	adantr 481	. . . . . . . . . . . 12 |- ( ( ph /\ a e. ( ( ( 1st ` Y ) ` X ) ( O Nat S ) F ) ) -> C e. Cat )
110	28	adantr 481	. . . . . . . . . . . 12 |- ( ( ph /\ a e. ( ( ( 1st ` Y ) ` X ) ( O Nat S ) F ) ) -> X e. B )
111		eqid 2622	. . . . . . . . . . . 12 |- (comp ` C ) = (comp ` C )
112	30	adantr 481	. . . . . . . . . . . 12 |- ( ( ph /\ a e. ( ( ( 1st ` Y ) ` X ) ( O Nat S ) F ) ) -> K e. ( P ( Hom ` C ) X ) )
113	100	adantr 481	. . . . . . . . . . . 12 |- ( ( ph /\ a e. ( ( ( 1st ` Y ) ` X ) ( O Nat S ) F ) ) -> ( .1. ` P ) e. ( P ( Hom ` C ) P ) )
114	16, 9, 109, 37, 13, 110, 111, 37, 112, 113	yon2 16906	. . . . . . . . . . 11 |- ( ( ph /\ a e. ( ( ( 1st ` Y ) ` X ) ( O Nat S ) F ) ) -> ( ( ( ( P ( 2nd ` Y ) X ) ` K ) ` P ) ` ( .1. ` P ) ) = ( K ( <. P , P >. (comp ` C ) X ) ( .1. ` P ) ) )
115	9, 13, 99, 109, 37, 111, 110, 112	catrid 16345	. . . . . . . . . . 11 |- ( ( ph /\ a e. ( ( ( 1st ` Y ) ` X ) ( O Nat S ) F ) ) -> ( K ( <. P , P >. (comp ` C ) X ) ( .1. ` P ) ) = K )
116	114, 115	eqtrd 2656	. . . . . . . . . 10 |- ( ( ph /\ a e. ( ( ( 1st ` Y ) ` X ) ( O Nat S ) F ) ) -> ( ( ( ( P ( 2nd ` Y ) X ) ` K ) ` P ) ` ( .1. ` P ) ) = K )
117	116	fveq2d 6195	. . . . . . . . 9 |- ( ( ph /\ a e. ( ( ( 1st ` Y ) ` X ) ( O Nat S ) F ) ) -> ( ( a ` P ) ` ( ( ( ( P ( 2nd ` Y ) X ) ` K ) ` P ) ` ( .1. ` P ) ) ) = ( ( a ` P ) ` K ) )
118		eqid 2622	. . . . . . . . . . . . . . 15 |- ( Hom ` O ) = ( Hom ` O )
119	10, 118, 70, 47, 28, 27	funcf2 16528	. . . . . . . . . . . . . 14 |- ( ph -> ( X ( 2nd ` ( ( 1st ` Y ) ` X ) ) P ) : ( X ( Hom ` O ) P ) --> ( ( ( 1st ` ( ( 1st ` Y ) ` X ) ) ` X ) ( Hom ` S ) ( ( 1st ` ( ( 1st ` Y ) ` X ) ) ` P ) ) )
120	13, 8	oppchom 16375	. . . . . . . . . . . . . . 15 |- ( X ( Hom ` O ) P ) = ( P ( Hom ` C ) X )
121	30, 120	syl6eleqr 2712	. . . . . . . . . . . . . 14 |- ( ph -> K e. ( X ( Hom ` O ) P ) )
122	119, 121	ffvelrnd 6360	. . . . . . . . . . . . 13 |- ( ph -> ( ( X ( 2nd ` ( ( 1st ` Y ) ` X ) ) P ) ` K ) e. ( ( ( 1st ` ( ( 1st ` Y ) ` X ) ) ` X ) ( Hom ` S ) ( ( 1st ` ( ( 1st ` Y ) ` X ) ) ` P ) ) )
123	51, 28	ffvelrnd 6360	. . . . . . . . . . . . . 14 |- ( ph -> ( ( 1st ` ( ( 1st ` Y ) ` X ) ) ` X ) e. U )
124	18, 22, 70, 123, 52	elsetchom 16731	. . . . . . . . . . . . 13 |- ( ph -> ( ( ( X ( 2nd ` ( ( 1st ` Y ) ` X ) ) P ) ` K ) e. ( ( ( 1st ` ( ( 1st ` Y ) ` X ) ) ` X ) ( Hom ` S ) ( ( 1st ` ( ( 1st ` Y ) ` X ) ) ` P ) ) <-> ( ( X ( 2nd ` ( ( 1st ` Y ) ` X ) ) P ) ` K ) : ( ( 1st ` ( ( 1st ` Y ) ` X ) ) ` X ) --> ( ( 1st ` ( ( 1st ` Y ) ` X ) ) ` P ) ) )
125	122, 124	mpbid 222	. . . . . . . . . . . 12 |- ( ph -> ( ( X ( 2nd ` ( ( 1st ` Y ) ` X ) ) P ) ` K ) : ( ( 1st ` ( ( 1st ` Y ) ` X ) ) ` X ) --> ( ( 1st ` ( ( 1st ` Y ) ` X ) ) ` P ) )
126	125	adantr 481	. . . . . . . . . . 11 |- ( ( ph /\ a e. ( ( ( 1st ` Y ) ` X ) ( O Nat S ) F ) ) -> ( ( X ( 2nd ` ( ( 1st ` Y ) ` X ) ) P ) ` K ) : ( ( 1st ` ( ( 1st ` Y ) ` X ) ) ` X ) --> ( ( 1st ` ( ( 1st ` Y ) ` X ) ) ` P ) )
127	9, 13, 99, 17, 28	catidcl 16343	. . . . . . . . . . . . 13 |- ( ph -> ( .1. ` X ) e. ( X ( Hom ` C ) X ) )
128	16, 9, 17, 28, 13, 28	yon11 16904	. . . . . . . . . . . . 13 |- ( ph -> ( ( 1st ` ( ( 1st ` Y ) ` X ) ) ` X ) = ( X ( Hom ` C ) X ) )
129	127, 128	eleqtrrd 2704	. . . . . . . . . . . 12 |- ( ph -> ( .1. ` X ) e. ( ( 1st ` ( ( 1st ` Y ) ` X ) ) ` X ) )
130	129	adantr 481	. . . . . . . . . . 11 |- ( ( ph /\ a e. ( ( ( 1st ` Y ) ` X ) ( O Nat S ) F ) ) -> ( .1. ` X ) e. ( ( 1st ` ( ( 1st ` Y ) ` X ) ) ` X ) )
131		fvco3 6275	. . . . . . . . . . 11 |- ( ( ( ( X ( 2nd ` ( ( 1st ` Y ) ` X ) ) P ) ` K ) : ( ( 1st ` ( ( 1st ` Y ) ` X ) ) ` X ) --> ( ( 1st ` ( ( 1st ` Y ) ` X ) ) ` P ) /\ ( .1. ` X ) e. ( ( 1st ` ( ( 1st ` Y ) ` X ) ) ` X ) ) -> ( ( ( a ` P ) o. ( ( X ( 2nd ` ( ( 1st ` Y ) ` X ) ) P ) ` K ) ) ` ( .1. ` X ) ) = ( ( a ` P ) ` ( ( ( X ( 2nd ` ( ( 1st ` Y ) ` X ) ) P ) ` K ) ` ( .1. ` X ) ) ) )
132	126, 130, 131	syl2anc 693	. . . . . . . . . 10 |- ( ( ph /\ a e. ( ( ( 1st ` Y ) ` X ) ( O Nat S ) F ) ) -> ( ( ( a ` P ) o. ( ( X ( 2nd ` ( ( 1st ` Y ) ` X ) ) P ) ` K ) ) ` ( .1. ` X ) ) = ( ( a ` P ) ` ( ( ( X ( 2nd ` ( ( 1st ` Y ) ` X ) ) P ) ` K ) ` ( .1. ` X ) ) ) )
133	121	adantr 481	. . . . . . . . . . . . 13 |- ( ( ph /\ a e. ( ( ( 1st ` Y ) ` X ) ( O Nat S ) F ) ) -> K e. ( X ( Hom ` O ) P ) )
134	7, 69, 10, 118, 11, 110, 37, 133	nati 16615	. . . . . . . . . . . 12 |- ( ( ph /\ a e. ( ( ( 1st ` Y ) ` X ) ( O Nat S ) F ) ) -> ( ( a ` P ) ( <. ( ( 1st ` ( ( 1st ` Y ) ` X ) ) ` X ) , ( ( 1st ` ( ( 1st ` Y ) ` X ) ) ` P ) >. (comp ` S ) ( ( 1st ` F ) ` P ) ) ( ( X ( 2nd ` ( ( 1st ` Y ) ` X ) ) P ) ` K ) ) = ( ( ( X ( 2nd ` F ) P ) ` K ) ( <. ( ( 1st ` ( ( 1st ` Y ) ` X ) ) ` X ) , ( ( 1st ` F ) ` X ) >. (comp ` S ) ( ( 1st ` F ) ` P ) ) ( a ` X ) ) )
135	123	adantr 481	. . . . . . . . . . . . 13 |- ( ( ph /\ a e. ( ( ( 1st ` Y ) ` X ) ( O Nat S ) F ) ) -> ( ( 1st ` ( ( 1st ` Y ) ` X ) ) ` X ) e. U )
136	18, 40, 11, 135, 53, 61, 126, 73	setcco 16733	. . . . . . . . . . . 12 |- ( ( ph /\ a e. ( ( ( 1st ` Y ) ` X ) ( O Nat S ) F ) ) -> ( ( a ` P ) ( <. ( ( 1st ` ( ( 1st ` Y ) ` X ) ) ` X ) , ( ( 1st ` ( ( 1st ` Y ) ` X ) ) ` P ) >. (comp ` S ) ( ( 1st ` F ) ` P ) ) ( ( X ( 2nd ` ( ( 1st ` Y ) ` X ) ) P ) ` K ) ) = ( ( a ` P ) o. ( ( X ( 2nd ` ( ( 1st ` Y ) ` X ) ) P ) ` K ) ) )
137	59, 28	ffvelrnd 6360	. . . . . . . . . . . . . 14 |- ( ph -> ( ( 1st ` F ) ` X ) e. U )
138	137	adantr 481	. . . . . . . . . . . . 13 |- ( ( ph /\ a e. ( ( ( 1st ` Y ) ` X ) ( O Nat S ) F ) ) -> ( ( 1st ` F ) ` X ) e. U )
139	7, 69, 10, 70, 110	natcl 16613	. . . . . . . . . . . . . 14 |- ( ( ph /\ a e. ( ( ( 1st ` Y ) ` X ) ( O Nat S ) F ) ) -> ( a ` X ) e. ( ( ( 1st ` ( ( 1st ` Y ) ` X ) ) ` X ) ( Hom ` S ) ( ( 1st ` F ) ` X ) ) )
140	18, 40, 70, 135, 138	elsetchom 16731	. . . . . . . . . . . . . 14 |- ( ( ph /\ a e. ( ( ( 1st ` Y ) ` X ) ( O Nat S ) F ) ) -> ( ( a ` X ) e. ( ( ( 1st ` ( ( 1st ` Y ) ` X ) ) ` X ) ( Hom ` S ) ( ( 1st ` F ) ` X ) ) <-> ( a ` X ) : ( ( 1st ` ( ( 1st ` Y ) ` X ) ) ` X ) --> ( ( 1st ` F ) ` X ) ) )
141	139, 140	mpbid 222	. . . . . . . . . . . . 13 |- ( ( ph /\ a e. ( ( ( 1st ` Y ) ` X ) ( O Nat S ) F ) ) -> ( a ` X ) : ( ( 1st ` ( ( 1st ` Y ) ` X ) ) ` X ) --> ( ( 1st ` F ) ` X ) )
142	10, 118, 70, 56, 28, 27	funcf2 16528	. . . . . . . . . . . . . . . 16 |- ( ph -> ( X ( 2nd ` F ) P ) : ( X ( Hom ` O ) P ) --> ( ( ( 1st ` F ) ` X ) ( Hom ` S ) ( ( 1st ` F ) ` P ) ) )
143	142, 121	ffvelrnd 6360	. . . . . . . . . . . . . . 15 |- ( ph -> ( ( X ( 2nd ` F ) P ) ` K ) e. ( ( ( 1st ` F ) ` X ) ( Hom ` S ) ( ( 1st ` F ) ` P ) ) )
144	18, 22, 70, 137, 60	elsetchom 16731	. . . . . . . . . . . . . . 15 |- ( ph -> ( ( ( X ( 2nd ` F ) P ) ` K ) e. ( ( ( 1st ` F ) ` X ) ( Hom ` S ) ( ( 1st ` F ) ` P ) ) <-> ( ( X ( 2nd ` F ) P ) ` K ) : ( ( 1st ` F ) ` X ) --> ( ( 1st ` F ) ` P ) ) )
145	143, 144	mpbid 222	. . . . . . . . . . . . . 14 |- ( ph -> ( ( X ( 2nd ` F ) P ) ` K ) : ( ( 1st ` F ) ` X ) --> ( ( 1st ` F ) ` P ) )
146	145	adantr 481	. . . . . . . . . . . . 13 |- ( ( ph /\ a e. ( ( ( 1st ` Y ) ` X ) ( O Nat S ) F ) ) -> ( ( X ( 2nd ` F ) P ) ` K ) : ( ( 1st ` F ) ` X ) --> ( ( 1st ` F ) ` P ) )
147	18, 40, 11, 135, 138, 61, 141, 146	setcco 16733	. . . . . . . . . . . 12 |- ( ( ph /\ a e. ( ( ( 1st ` Y ) ` X ) ( O Nat S ) F ) ) -> ( ( ( X ( 2nd ` F ) P ) ` K ) ( <. ( ( 1st ` ( ( 1st ` Y ) ` X ) ) ` X ) , ( ( 1st ` F ) ` X ) >. (comp ` S ) ( ( 1st ` F ) ` P ) ) ( a ` X ) ) = ( ( ( X ( 2nd ` F ) P ) ` K ) o. ( a ` X ) ) )
148	134, 136, 147	3eqtr3d 2664	. . . . . . . . . . 11 |- ( ( ph /\ a e. ( ( ( 1st ` Y ) ` X ) ( O Nat S ) F ) ) -> ( ( a ` P ) o. ( ( X ( 2nd ` ( ( 1st ` Y ) ` X ) ) P ) ` K ) ) = ( ( ( X ( 2nd ` F ) P ) ` K ) o. ( a ` X ) ) )
149	148	fveq1d 6193	. . . . . . . . . 10 |- ( ( ph /\ a e. ( ( ( 1st ` Y ) ` X ) ( O Nat S ) F ) ) -> ( ( ( a ` P ) o. ( ( X ( 2nd ` ( ( 1st ` Y ) ` X ) ) P ) ` K ) ) ` ( .1. ` X ) ) = ( ( ( ( X ( 2nd ` F ) P ) ` K ) o. ( a ` X ) ) ` ( .1. ` X ) ) )
150	127	adantr 481	. . . . . . . . . . . . 13 |- ( ( ph /\ a e. ( ( ( 1st ` Y ) ` X ) ( O Nat S ) F ) ) -> ( .1. ` X ) e. ( X ( Hom ` C ) X ) )
151	16, 9, 109, 110, 13, 110, 111, 37, 112, 150	yon12 16905	. . . . . . . . . . . 12 |- ( ( ph /\ a e. ( ( ( 1st ` Y ) ` X ) ( O Nat S ) F ) ) -> ( ( ( X ( 2nd ` ( ( 1st ` Y ) ` X ) ) P ) ` K ) ` ( .1. ` X ) ) = ( ( .1. ` X ) ( <. P , X >. (comp ` C ) X ) K ) )
152	9, 13, 99, 109, 37, 111, 110, 112	catlid 16344	. . . . . . . . . . . 12 |- ( ( ph /\ a e. ( ( ( 1st ` Y ) ` X ) ( O Nat S ) F ) ) -> ( ( .1. ` X ) ( <. P , X >. (comp ` C ) X ) K ) = K )
153	151, 152	eqtrd 2656	. . . . . . . . . . 11 |- ( ( ph /\ a e. ( ( ( 1st ` Y ) ` X ) ( O Nat S ) F ) ) -> ( ( ( X ( 2nd ` ( ( 1st ` Y ) ` X ) ) P ) ` K ) ` ( .1. ` X ) ) = K )
154	153	fveq2d 6195	. . . . . . . . . 10 |- ( ( ph /\ a e. ( ( ( 1st ` Y ) ` X ) ( O Nat S ) F ) ) -> ( ( a ` P ) ` ( ( ( X ( 2nd ` ( ( 1st ` Y ) ` X ) ) P ) ` K ) ` ( .1. ` X ) ) ) = ( ( a ` P ) ` K ) )
155	132, 149, 154	3eqtr3d 2664	. . . . . . . . 9 |- ( ( ph /\ a e. ( ( ( 1st ` Y ) ` X ) ( O Nat S ) F ) ) -> ( ( ( ( X ( 2nd ` F ) P ) ` K ) o. ( a ` X ) ) ` ( .1. ` X ) ) = ( ( a ` P ) ` K ) )
156		fvco3 6275	. . . . . . . . . 10 |- ( ( ( a ` X ) : ( ( 1st ` ( ( 1st ` Y ) ` X ) ) ` X ) --> ( ( 1st ` F ) ` X ) /\ ( .1. ` X ) e. ( ( 1st ` ( ( 1st ` Y ) ` X ) ) ` X ) ) -> ( ( ( ( X ( 2nd ` F ) P ) ` K ) o. ( a ` X ) ) ` ( .1. ` X ) ) = ( ( ( X ( 2nd ` F ) P ) ` K ) ` ( ( a ` X ) ` ( .1. ` X ) ) ) )
157	141, 130, 156	syl2anc 693	. . . . . . . . 9 |- ( ( ph /\ a e. ( ( ( 1st ` Y ) ` X ) ( O Nat S ) F ) ) -> ( ( ( ( X ( 2nd ` F ) P ) ` K ) o. ( a ` X ) ) ` ( .1. ` X ) ) = ( ( ( X ( 2nd ` F ) P ) ` K ) ` ( ( a ` X ) ` ( .1. ` X ) ) ) )
158	117, 155, 157	3eqtr2d 2662	. . . . . . . 8 |- ( ( ph /\ a e. ( ( ( 1st ` Y ) ` X ) ( O Nat S ) F ) ) -> ( ( a ` P ) ` ( ( ( ( P ( 2nd ` Y ) X ) ` K ) ` P ) ` ( .1. ` P ) ) ) = ( ( ( X ( 2nd ` F ) P ) ` K ) ` ( ( a ` X ) ` ( .1. ` X ) ) ) )
159	158	fveq2d 6195	. . . . . . 7 |- ( ( ph /\ a e. ( ( ( 1st ` Y ) ` X ) ( O Nat S ) F ) ) -> ( ( A ` P ) ` ( ( a ` P ) ` ( ( ( ( P ( 2nd ` Y ) X ) ` K ) ` P ) ` ( .1. ` P ) ) ) ) = ( ( A ` P ) ` ( ( ( X ( 2nd ` F ) P ) ` K ) ` ( ( a ` X ) ` ( .1. ` X ) ) ) ) )
160	108, 159	eqtrd 2656	. . . . . 6 |- ( ( ph /\ a e. ( ( ( 1st ` Y ) ` X ) ( O Nat S ) F ) ) -> ( ( ( A ` P ) o. ( a ` P ) ) ` ( ( ( ( P ( 2nd ` Y ) X ) ` K ) ` P ) ` ( .1. ` P ) ) ) = ( ( A ` P ) ` ( ( ( X ( 2nd ` F ) P ) ` K ) ` ( ( a ` X ) ` ( .1. ` X ) ) ) ) )
161	98, 105, 160	3eqtrd 2660	. . . . 5 |- ( ( ph /\ a e. ( ( ( 1st ` Y ) ` X ) ( O Nat S ) F ) ) -> ( ( ( ( A ( <. ( ( 1st ` Y ) ` X ) , F >. (comp ` Q ) G ) a ) ( <. ( ( 1st ` Y ) ` P ) , ( ( 1st ` Y ) ` X ) >. (comp ` Q ) G ) ( ( P ( 2nd ` Y ) X ) ` K ) ) ` P ) ` ( .1. ` P ) ) = ( ( A ` P ) ` ( ( ( X ( 2nd ` F ) P ) ` K ) ` ( ( a ` X ) ` ( .1. ` X ) ) ) ) )
162	161	mpteq2dva 4744	. . . 4 |- ( ph -> ( a e. ( ( ( 1st ` Y ) ` X ) ( O Nat S ) F ) |-> ( ( ( ( A ( <. ( ( 1st ` Y ) ` X ) , F >. (comp ` Q ) G ) a ) ( <. ( ( 1st ` Y ) ` P ) , ( ( 1st ` Y ) ` X ) >. (comp ` Q ) G ) ( ( P ( 2nd ` Y ) X ) ` K ) ) ` P ) ` ( .1. ` P ) ) ) = ( a e. ( ( ( 1st ` Y ) ` X ) ( O Nat S ) F ) |-> ( ( A ` P ) ` ( ( ( X ( 2nd ` F ) P ) ` K ) ` ( ( a ` X ) ` ( .1. ` X ) ) ) ) ) )
163	5, 162	syl5eq 2668	. . 3 |- ( ph -> ( b e. ( ( ( 1st ` Y ) ` X ) ( O Nat S ) F ) |-> ( ( ( ( A ( <. ( ( 1st ` Y ) ` X ) , F >. (comp ` Q ) G ) b ) ( <. ( ( 1st ` Y ) ` P ) , ( ( 1st ` Y ) ` X ) >. (comp ` Q ) G ) ( ( P ( 2nd ` Y ) X ) ` K ) ) ` P ) ` ( .1. ` P ) ) ) = ( a e. ( ( ( 1st ` Y ) ` X ) ( O Nat S ) F ) |-> ( ( A ` P ) ` ( ( ( X ( 2nd ` F ) P ) ` K ) ` ( ( a ` X ) ` ( .1. ` X ) ) ) ) ) )
164		eqid 2622	. . . . . . . . . . 11 |- ( Q X.c O ) = ( Q X.c O )
165	164, 43, 10	xpcbas 16818	. . . . . . . . . 10 |- ( ( O Func S ) X. B ) = ( Base ` ( Q X.c O ) )
166		eqid 2622	. . . . . . . . . 10 |- ( Hom ` ( Q X.c O ) ) = ( Hom ` ( Q X.c O ) )
167		eqid 2622	. . . . . . . . . 10 |- ( Hom ` T ) = ( Hom ` T )
168		relfunc 16522	. . . . . . . . . . 11 |- Rel ( ( Q X.c O ) Func T )
169		yoneda.t	. . . . . . . . . . . . 13 |- T = ( SetCat ` V )
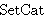170		yoneda.h	. . . . . . . . . . . . 13 |- H = (HomF ` Q )
171		yoneda.r	. . . . . . . . . . . . 13 |- R = ( ( Q X.c O ) FuncCat T )
172		yoneda.e	. . . . . . . . . . . . 13 |- E = ( O evalF S )
173		yoneda.z	. . . . . . . . . . . . 13 |- Z = ( H o.func ( ( <. ( 1st ` Y ) , tpos ( 2nd ` Y ) >. o.func ( Q 2ndF O ) ) ⟨,⟩F ( Q 1stF O ) ) )
174	16, 9, 99, 8, 18, 169, 6, 170, 171, 172, 173, 17, 19, 23, 20	yonedalem1 16912	. . . . . . . . . . . 12 |- ( ph -> ( Z e. ( ( Q X.c O ) Func T ) /\ E e. ( ( Q X.c O ) Func T ) ) )
175	174	simpld 475	. . . . . . . . . . 11 |- ( ph -> Z e. ( ( Q X.c O ) Func T ) )
176		1st2ndbr 7217	. . . . . . . . . . 11 |- ( ( Rel ( ( Q X.c O ) Func T ) /\ Z e. ( ( Q X.c O ) Func T ) ) -> ( 1st ` Z ) ( ( Q X.c O ) Func T ) ( 2nd ` Z ) )
177	168, 175, 176	sylancr 695	. . . . . . . . . 10 |- ( ph -> ( 1st ` Z ) ( ( Q X.c O ) Func T ) ( 2nd ` Z ) )
178		opelxpi 5148	. . . . . . . . . . 11 |- ( ( F e. ( O Func S ) /\ X e. B ) -> <. F , X >. e. ( ( O Func S ) X. B ) )
179	54, 28, 178	syl2anc 693	. . . . . . . . . 10 |- ( ph -> <. F , X >. e. ( ( O Func S ) X. B ) )
180		opelxpi 5148	. . . . . . . . . . 11 |- ( ( G e. ( O Func S ) /\ P e. B ) -> <. G , P >. e. ( ( O Func S ) X. B ) )
181	62, 27, 180	syl2anc 693	. . . . . . . . . 10 |- ( ph -> <. G , P >. e. ( ( O Func S ) X. B ) )
182	165, 166, 167, 177, 179, 181	funcf2 16528	. . . . . . . . 9 |- ( ph -> ( <. F , X >. ( 2nd ` Z ) <. G , P >. ) : ( <. F , X >. ( Hom ` ( Q X.c O ) ) <. G , P >. ) --> ( ( ( 1st ` Z ) ` <. F , X >. ) ( Hom ` T ) ( ( 1st ` Z ) ` <. G , P >. ) ) )
183	164, 43, 10, 14, 118, 54, 28, 62, 27, 166	xpchom2 16826	. . . . . . . . . . 11 |- ( ph -> ( <. F , X >. ( Hom ` ( Q X.c O ) ) <. G , P >. ) = ( ( F ( O Nat S ) G ) X. ( X ( Hom ` O ) P ) ) )
184	120	xpeq2i 5136	. . . . . . . . . . 11 |- ( ( F ( O Nat S ) G ) X. ( X ( Hom ` O ) P ) ) = ( ( F ( O Nat S ) G ) X. ( P ( Hom ` C ) X ) )
185	183, 184	syl6eq 2672	. . . . . . . . . 10 |- ( ph -> ( <. F , X >. ( Hom ` ( Q X.c O ) ) <. G , P >. ) = ( ( F ( O Nat S ) G ) X. ( P ( Hom ` C ) X ) ) )
186		df-ov 6653	. . . . . . . . . . . . 13 |- ( F ( 1st ` Z ) X ) = ( ( 1st ` Z ) ` <. F , X >. )
187		df-ov 6653	. . . . . . . . . . . . 13 |- ( G ( 1st ` Z ) P ) = ( ( 1st ` Z ) ` <. G , P >. )
188	186, 187	oveq12i 6662	. . . . . . . . . . . 12 |- ( ( F ( 1st ` Z ) X ) ( Hom ` T ) ( G ( 1st ` Z ) P ) ) = ( ( ( 1st ` Z ) ` <. F , X >. ) ( Hom ` T ) ( ( 1st ` Z ) ` <. G , P >. ) )
189	188	eqcomi 2631	. . . . . . . . . . 11 |- ( ( ( 1st ` Z ) ` <. F , X >. ) ( Hom ` T ) ( ( 1st ` Z ) ` <. G , P >. ) ) = ( ( F ( 1st ` Z ) X ) ( Hom ` T ) ( G ( 1st ` Z ) P ) )
190	189	a1i 11	. . . . . . . . . 10 |- ( ph -> ( ( ( 1st ` Z ) ` <. F , X >. ) ( Hom ` T ) ( ( 1st ` Z ) ` <. G , P >. ) ) = ( ( F ( 1st ` Z ) X ) ( Hom ` T ) ( G ( 1st ` Z ) P ) ) )
191	185, 190	feq23d 6040	. . . . . . . . 9 |- ( ph -> ( ( <. F , X >. ( 2nd ` Z ) <. G , P >. ) : ( <. F , X >. ( Hom ` ( Q X.c O ) ) <. G , P >. ) --> ( ( ( 1st ` Z ) ` <. F , X >. ) ( Hom ` T ) ( ( 1st ` Z ) ` <. G , P >. ) ) <-> ( <. F , X >. ( 2nd ` Z ) <. G , P >. ) : ( ( F ( O Nat S ) G ) X. ( P ( Hom ` C ) X ) ) --> ( ( F ( 1st ` Z ) X ) ( Hom ` T ) ( G ( 1st ` Z ) P ) ) ) )
192	182, 191	mpbid 222	. . . . . . . 8 |- ( ph -> ( <. F , X >. ( 2nd ` Z ) <. G , P >. ) : ( ( F ( O Nat S ) G ) X. ( P ( Hom ` C ) X ) ) --> ( ( F ( 1st ` Z ) X ) ( Hom ` T ) ( G ( 1st ` Z ) P ) ) )
193	192, 34, 30	fovrnd 6806	. . . . . . 7 |- ( ph -> ( A ( <. F , X >. ( 2nd ` Z ) <. G , P >. ) K ) e. ( ( F ( 1st ` Z ) X ) ( Hom ` T ) ( G ( 1st ` Z ) P ) ) )
194		eqid 2622	. . . . . . . . . . 11 |- ( Base ` T ) = ( Base ` T )
195	165, 194, 177	funcf1 16526	. . . . . . . . . 10 |- ( ph -> ( 1st ` Z ) : ( ( O Func S ) X. B ) --> ( Base ` T ) )
196	195, 54, 28	fovrnd 6806	. . . . . . . . 9 |- ( ph -> ( F ( 1st ` Z ) X ) e. ( Base ` T ) )
197	169, 19	setcbas 16728	. . . . . . . . 9 |- ( ph -> V = ( Base ` T ) )
198	196, 197	eleqtrrd 2704	. . . . . . . 8 |- ( ph -> ( F ( 1st ` Z ) X ) e. V )
199	195, 62, 27	fovrnd 6806	. . . . . . . . 9 |- ( ph -> ( G ( 1st ` Z ) P ) e. ( Base ` T ) )
200	199, 197	eleqtrrd 2704	. . . . . . . 8 |- ( ph -> ( G ( 1st ` Z ) P ) e. V )
201	169, 19, 167, 198, 200	elsetchom 16731	. . . . . . 7 |- ( ph -> ( ( A ( <. F , X >. ( 2nd ` Z ) <. G , P >. ) K ) e. ( ( F ( 1st ` Z ) X ) ( Hom ` T ) ( G ( 1st ` Z ) P ) ) <-> ( A ( <. F , X >. ( 2nd ` Z ) <. G , P >. ) K ) : ( F ( 1st ` Z ) X ) --> ( G ( 1st ` Z ) P ) ) )
202	193, 201	mpbid 222	. . . . . 6 |- ( ph -> ( A ( <. F , X >. ( 2nd ` Z ) <. G , P >. ) K ) : ( F ( 1st ` Z ) X ) --> ( G ( 1st ` Z ) P ) )
203	16, 9, 99, 8, 18, 169, 6, 170, 171, 172, 173, 17, 19, 23, 20, 54, 28, 62, 27, 34, 30	yonedalem22 16918	. . . . . . . 8 |- ( ph -> ( A ( <. F , X >. ( 2nd ` Z ) <. G , P >. ) K ) = ( ( ( P ( 2nd ` Y ) X ) ` K ) ( <. ( ( 1st ` Y ) ` X ) , F >. ( 2nd ` H ) <. ( ( 1st ` Y ) ` P ) , G >. ) A ) )
204	8	oppccat 16382	. . . . . . . . . . 11 |- ( C e. Cat -> O e. Cat )
205	17, 204	syl 17	. . . . . . . . . 10 |- ( ph -> O e. Cat )
206	18	setccat 16735	. . . . . . . . . . 11 |- ( U e. _V -> S e. Cat )
207	22, 206	syl 17	. . . . . . . . . 10 |- ( ph -> S e. Cat )
208	6, 205, 207	fuccat 16630	. . . . . . . . 9 |- ( ph -> Q e. Cat )
209	170, 208, 43, 14, 45, 54, 82, 62, 12, 31, 34	hof2val 16896	. . . . . . . 8 |- ( ph -> ( ( ( P ( 2nd ` Y ) X ) ` K ) ( <. ( ( 1st ` Y ) ` X ) , F >. ( 2nd ` H ) <. ( ( 1st ` Y ) ` P ) , G >. ) A ) = ( b e. ( ( ( 1st ` Y ) ` X ) ( O Nat S ) F ) |-> ( ( A ( <. ( ( 1st ` Y ) ` X ) , F >. (comp ` Q ) G ) b ) ( <. ( ( 1st ` Y ) ` P ) , ( ( 1st ` Y ) ` X ) >. (comp ` Q ) G ) ( ( P ( 2nd ` Y ) X ) ` K ) ) ) )
210	203, 209	eqtrd 2656	. . . . . . 7 |- ( ph -> ( A ( <. F , X >. ( 2nd ` Z ) <. G , P >. ) K ) = ( b e. ( ( ( 1st ` Y ) ` X ) ( O Nat S ) F ) |-> ( ( A ( <. ( ( 1st ` Y ) ` X ) , F >. (comp ` Q ) G ) b ) ( <. ( ( 1st ` Y ) ` P ) , ( ( 1st ` Y ) ` X ) >. (comp ` Q ) G ) ( ( P ( 2nd ` Y ) X ) ` K ) ) ) )
211	16, 9, 99, 8, 18, 169, 6, 170, 171, 172, 173, 17, 19, 23, 20, 54, 28	yonedalem21 16913	. . . . . . 7 |- ( ph -> ( F ( 1st ` Z ) X ) = ( ( ( 1st ` Y ) ` X ) ( O Nat S ) F ) )
212	16, 9, 99, 8, 18, 169, 6, 170, 171, 172, 173, 17, 19, 23, 20, 62, 27	yonedalem21 16913	. . . . . . 7 |- ( ph -> ( G ( 1st ` Z ) P ) = ( ( ( 1st ` Y ) ` P ) ( O Nat S ) G ) )
213	210, 211, 212	feq123d 6034	. . . . . 6 |- ( ph -> ( ( A ( <. F , X >. ( 2nd ` Z ) <. G , P >. ) K ) : ( F ( 1st ` Z ) X ) --> ( G ( 1st ` Z ) P ) <-> ( b e. ( ( ( 1st ` Y ) ` X ) ( O Nat S ) F ) |-> ( ( A ( <. ( ( 1st ` Y ) ` X ) , F >. (comp ` Q ) G ) b ) ( <. ( ( 1st ` Y ) ` P ) , ( ( 1st ` Y ) ` X ) >. (comp ` Q ) G ) ( ( P ( 2nd ` Y ) X ) ` K ) ) ) : ( ( ( 1st ` Y ) ` X ) ( O Nat S ) F ) --> ( ( ( 1st ` Y ) ` P ) ( O Nat S ) G ) ) )
214	202, 213	mpbid 222	. . . . 5 |- ( ph -> ( b e. ( ( ( 1st ` Y ) ` X ) ( O Nat S ) F ) |-> ( ( A ( <. ( ( 1st ` Y ) ` X ) , F >. (comp ` Q ) G ) b ) ( <. ( ( 1st ` Y ) ` P ) , ( ( 1st ` Y ) ` X ) >. (comp ` Q ) G ) ( ( P ( 2nd ` Y ) X ) ` K ) ) ) : ( ( ( 1st ` Y ) ` X ) ( O Nat S ) F ) --> ( ( ( 1st ` Y ) ` P ) ( O Nat S ) G ) )
215		eqid 2622	. . . . . 6 |- ( b e. ( ( ( 1st ` Y ) ` X ) ( O Nat S ) F ) |-> ( ( A ( <. ( ( 1st ` Y ) ` X ) , F >. (comp ` Q ) G ) b ) ( <. ( ( 1st ` Y ) ` P ) , ( ( 1st ` Y ) ` X ) >. (comp ` Q ) G ) ( ( P ( 2nd ` Y ) X ) ` K ) ) ) = ( b e. ( ( ( 1st ` Y ) ` X ) ( O Nat S ) F ) |-> ( ( A ( <. ( ( 1st ` Y ) ` X ) , F >. (comp ` Q ) G ) b ) ( <. ( ( 1st ` Y ) ` P ) , ( ( 1st ` Y ) ` X ) >. (comp ` Q ) G ) ( ( P ( 2nd ` Y ) X ) ` K ) ) )
216	215	fmpt 6381	. . . . 5 |- ( A. b e. ( ( ( 1st ` Y ) ` X ) ( O Nat S ) F ) ( ( A ( <. ( ( 1st ` Y ) ` X ) , F >. (comp ` Q ) G ) b ) ( <. ( ( 1st ` Y ) ` P ) , ( ( 1st ` Y ) ` X ) >. (comp ` Q ) G ) ( ( P ( 2nd ` Y ) X ) ` K ) ) e. ( ( ( 1st ` Y ) ` P ) ( O Nat S ) G ) <-> ( b e. ( ( ( 1st ` Y ) ` X ) ( O Nat S ) F ) |-> ( ( A ( <. ( ( 1st ` Y ) ` X ) , F >. (comp ` Q ) G ) b ) ( <. ( ( 1st ` Y ) ` P ) , ( ( 1st ` Y ) ` X ) >. (comp ` Q ) G ) ( ( P ( 2nd ` Y ) X ) ` K ) ) ) : ( ( ( 1st ` Y ) ` X ) ( O Nat S ) F ) --> ( ( ( 1st ` Y ) ` P ) ( O Nat S ) G ) )
217	214, 216	sylibr 224	. . . 4 |- ( ph -> A. b e. ( ( ( 1st ` Y ) ` X ) ( O Nat S ) F ) ( ( A ( <. ( ( 1st ` Y ) ` X ) , F >. (comp ` Q ) G ) b ) ( <. ( ( 1st ` Y ) ` P ) , ( ( 1st ` Y ) ` X ) >. (comp ` Q ) G ) ( ( P ( 2nd ` Y ) X ) ` K ) ) e. ( ( ( 1st ` Y ) ` P ) ( O Nat S ) G ) )
218		yonedalem3.m	. . . . . 6 |- M = ( f e. ( O Func S ) , x e. B |-> ( a e. ( ( ( 1st ` Y ) ` x ) ( O Nat S ) f ) |-> ( ( a ` x ) ` ( .1. ` x ) ) ) )
219	16, 9, 99, 8, 18, 169, 6, 170, 171, 172, 173, 17, 19, 23, 20, 62, 27, 218	yonedalem3a 16914	. . . . 5 |- ( ph -> ( ( G M P ) = ( a e. ( ( ( 1st ` Y ) ` P ) ( O Nat S ) G ) |-> ( ( a ` P ) ` ( .1. ` P ) ) ) /\ ( G M P ) : ( G ( 1st ` Z ) P ) --> ( G ( 1st ` E ) P ) ) )
220	219	simpld 475	. . . 4 |- ( ph -> ( G M P ) = ( a e. ( ( ( 1st ` Y ) ` P ) ( O Nat S ) G ) |-> ( ( a ` P ) ` ( .1. ` P ) ) ) )
221		fveq1 6190	. . . . 5 |- ( a = ( ( A ( <. ( ( 1st ` Y ) ` X ) , F >. (comp ` Q ) G ) b ) ( <. ( ( 1st ` Y ) ` P ) , ( ( 1st ` Y ) ` X ) >. (comp ` Q ) G ) ( ( P ( 2nd ` Y ) X ) ` K ) ) -> ( a ` P ) = ( ( ( A ( <. ( ( 1st ` Y ) ` X ) , F >. (comp ` Q ) G ) b ) ( <. ( ( 1st ` Y ) ` P ) , ( ( 1st ` Y ) ` X ) >. (comp ` Q ) G ) ( ( P ( 2nd ` Y ) X ) ` K ) ) ` P ) )
222	221	fveq1d 6193	. . . 4 |- ( a = ( ( A ( <. ( ( 1st ` Y ) ` X ) , F >. (comp ` Q ) G ) b ) ( <. ( ( 1st ` Y ) ` P ) , ( ( 1st ` Y ) ` X ) >. (comp ` Q ) G ) ( ( P ( 2nd ` Y ) X ) ` K ) ) -> ( ( a ` P ) ` ( .1. ` P ) ) = ( ( ( ( A ( <. ( ( 1st ` Y ) ` X ) , F >. (comp ` Q ) G ) b ) ( <. ( ( 1st ` Y ) ` P ) , ( ( 1st ` Y ) ` X ) >. (comp ` Q ) G ) ( ( P ( 2nd ` Y ) X ) ` K ) ) ` P ) ` ( .1. ` P ) ) )
223	217, 210, 220, 222	fmptcof 6397	. . 3 |- ( ph -> ( ( G M P ) o. ( A ( <. F , X >. ( 2nd ` Z ) <. G , P >. ) K ) ) = ( b e. ( ( ( 1st ` Y ) ` X ) ( O Nat S ) F ) |-> ( ( ( ( A ( <. ( ( 1st ` Y ) ` X ) , F >. (comp ` Q ) G ) b ) ( <. ( ( 1st ` Y ) ` P ) , ( ( 1st ` Y ) ` X ) >. (comp ` Q ) G ) ( ( P ( 2nd ` Y ) X ) ` K ) ) ` P ) ` ( .1. ` P ) ) ) )
224		eqid 2622	. . . . . . 7 |- ( <. F , X >. ( 2nd ` E ) <. G , P >. ) = ( <. F , X >. ( 2nd ` E ) <. G , P >. )
225	172, 205, 207, 10, 118, 11, 7, 54, 62, 28, 27, 224, 34, 121	evlf2val 16859	. . . . . 6 |- ( ph -> ( A ( <. F , X >. ( 2nd ` E ) <. G , P >. ) K ) = ( ( A ` P ) ( <. ( ( 1st ` F ) ` X ) , ( ( 1st ` F ) ` P ) >. (comp ` S ) ( ( 1st ` G ) ` P ) ) ( ( X ( 2nd ` F ) P ) ` K ) ) )
226	18, 22, 11, 137, 60, 67, 145, 77	setcco 16733	. . . . . 6 |- ( ph -> ( ( A ` P ) ( <. ( ( 1st ` F ) ` X ) , ( ( 1st ` F ) ` P ) >. (comp ` S ) ( ( 1st ` G ) ` P ) ) ( ( X ( 2nd ` F ) P ) ` K ) ) = ( ( A ` P ) o. ( ( X ( 2nd ` F ) P ) ` K ) ) )
227	225, 226	eqtrd 2656	. . . . 5 |- ( ph -> ( A ( <. F , X >. ( 2nd ` E ) <. G , P >. ) K ) = ( ( A ` P ) o. ( ( X ( 2nd ` F ) P ) ` K ) ) )
228	227	coeq1d 5283	. . . 4 |- ( ph -> ( ( A ( <. F , X >. ( 2nd ` E ) <. G , P >. ) K ) o. ( F M X ) ) = ( ( ( A ` P ) o. ( ( X ( 2nd ` F ) P ) ` K ) ) o. ( F M X ) ) )
229	16, 9, 99, 8, 18, 169, 6, 170, 171, 172, 173, 17, 19, 23, 20, 54, 28, 218	yonedalem3a 16914	. . . . . . . 8 |- ( ph -> ( ( F M X ) = ( a e. ( ( ( 1st ` Y ) ` X ) ( O Nat S ) F ) |-> ( ( a ` X ) ` ( .1. ` X ) ) ) /\ ( F M X ) : ( F ( 1st ` Z ) X ) --> ( F ( 1st ` E ) X ) ) )
230	229	simprd 479	. . . . . . 7 |- ( ph -> ( F M X ) : ( F ( 1st ` Z ) X ) --> ( F ( 1st ` E ) X ) )
231	229	simpld 475	. . . . . . . 8 |- ( ph -> ( F M X ) = ( a e. ( ( ( 1st ` Y ) ` X ) ( O Nat S ) F ) |-> ( ( a ` X ) ` ( .1. ` X ) ) ) )
232	172, 205, 207, 10, 54, 28	evlf1 16860	. . . . . . . 8 |- ( ph -> ( F ( 1st ` E ) X ) = ( ( 1st ` F ) ` X ) )
233	231, 211, 232	feq123d 6034	. . . . . . 7 |- ( ph -> ( ( F M X ) : ( F ( 1st ` Z ) X ) --> ( F ( 1st ` E ) X ) <-> ( a e. ( ( ( 1st ` Y ) ` X ) ( O Nat S ) F ) |-> ( ( a ` X ) ` ( .1. ` X ) ) ) : ( ( ( 1st ` Y ) ` X ) ( O Nat S ) F ) --> ( ( 1st ` F ) ` X ) ) )
234	230, 233	mpbid 222	. . . . . 6 |- ( ph -> ( a e. ( ( ( 1st ` Y ) ` X ) ( O Nat S ) F ) |-> ( ( a ` X ) ` ( .1. ` X ) ) ) : ( ( ( 1st ` Y ) ` X ) ( O Nat S ) F ) --> ( ( 1st ` F ) ` X ) )
235		eqid 2622	. . . . . . 7 |- ( a e. ( ( ( 1st ` Y ) ` X ) ( O Nat S ) F ) |-> ( ( a ` X ) ` ( .1. ` X ) ) ) = ( a e. ( ( ( 1st ` Y ) ` X ) ( O Nat S ) F ) |-> ( ( a ` X ) ` ( .1. ` X ) ) )
236	235	fmpt 6381	. . . . . 6 |- ( A. a e. ( ( ( 1st ` Y ) ` X ) ( O Nat S ) F ) ( ( a ` X ) ` ( .1. ` X ) ) e. ( ( 1st ` F ) ` X ) <-> ( a e. ( ( ( 1st ` Y ) ` X ) ( O Nat S ) F ) |-> ( ( a ` X ) ` ( .1. ` X ) ) ) : ( ( ( 1st ` Y ) ` X ) ( O Nat S ) F ) --> ( ( 1st ` F ) ` X ) )
237	234, 236	sylibr 224	. . . . 5 |- ( ph -> A. a e. ( ( ( 1st ` Y ) ` X ) ( O Nat S ) F ) ( ( a ` X ) ` ( .1. ` X ) ) e. ( ( 1st ` F ) ` X ) )
238		fcompt 6400	. . . . . 6 |- ( ( ( A ` P ) : ( ( 1st ` F ) ` P ) --> ( ( 1st ` G ) ` P ) /\ ( ( X ( 2nd ` F ) P ) ` K ) : ( ( 1st ` F ) ` X ) --> ( ( 1st ` F ) ` P ) ) -> ( ( A ` P ) o. ( ( X ( 2nd ` F ) P ) ` K ) ) = ( y e. ( ( 1st ` F ) ` X ) |-> ( ( A ` P ) ` ( ( ( X ( 2nd ` F ) P ) ` K ) ` y ) ) ) )
239	77, 145, 238	syl2anc 693	. . . . 5 |- ( ph -> ( ( A ` P ) o. ( ( X ( 2nd ` F ) P ) ` K ) ) = ( y e. ( ( 1st ` F ) ` X ) |-> ( ( A ` P ) ` ( ( ( X ( 2nd ` F ) P ) ` K ) ` y ) ) ) )
240		fveq2 6191	. . . . . 6 |- ( y = ( ( a ` X ) ` ( .1. ` X ) ) -> ( ( ( X ( 2nd ` F ) P ) ` K ) ` y ) = ( ( ( X ( 2nd ` F ) P ) ` K ) ` ( ( a ` X ) ` ( .1. ` X ) ) ) )
241	240	fveq2d 6195	. . . . 5 |- ( y = ( ( a ` X ) ` ( .1. ` X ) ) -> ( ( A ` P ) ` ( ( ( X ( 2nd ` F ) P ) ` K ) ` y ) ) = ( ( A ` P ) ` ( ( ( X ( 2nd ` F ) P ) ` K ) ` ( ( a ` X ) ` ( .1. ` X ) ) ) ) )
242	237, 231, 239, 241	fmptcof 6397	. . . 4 |- ( ph -> ( ( ( A ` P ) o. ( ( X ( 2nd ` F ) P ) ` K ) ) o. ( F M X ) ) = ( a e. ( ( ( 1st ` Y ) ` X ) ( O Nat S ) F ) |-> ( ( A ` P ) ` ( ( ( X ( 2nd ` F ) P ) ` K ) ` ( ( a ` X ) ` ( .1. ` X ) ) ) ) ) )
243	228, 242	eqtrd 2656	. . 3 |- ( ph -> ( ( A ( <. F , X >. ( 2nd ` E ) <. G , P >. ) K ) o. ( F M X ) ) = ( a e. ( ( ( 1st ` Y ) ` X ) ( O Nat S ) F ) |-> ( ( A ` P ) ` ( ( ( X ( 2nd ` F ) P ) ` K ) ` ( ( a ` X ) ` ( .1. ` X ) ) ) ) ) )
244	163, 223, 243	3eqtr4d 2666	. 2 |- ( ph -> ( ( G M P ) o. ( A ( <. F , X >. ( 2nd ` Z ) <. G , P >. ) K ) ) = ( ( A ( <. F , X >. ( 2nd ` E ) <. G , P >. ) K ) o. ( F M X ) ) )
245		eqid 2622	. . 3 |- (comp ` T ) = (comp ` T )
246	174	simprd 479	. . . . . . 7 |- ( ph -> E e. ( ( Q X.c O ) Func T ) )
247		1st2ndbr 7217	. . . . . . 7 |- ( ( Rel ( ( Q X.c O ) Func T ) /\ E e. ( ( Q X.c O ) Func T ) ) -> ( 1st ` E ) ( ( Q X.c O ) Func T ) ( 2nd ` E ) )
248	168, 246, 247	sylancr 695	. . . . . 6 |- ( ph -> ( 1st ` E ) ( ( Q X.c O ) Func T ) ( 2nd ` E ) )
249	165, 194, 248	funcf1 16526	. . . . 5 |- ( ph -> ( 1st ` E ) : ( ( O Func S ) X. B ) --> ( Base ` T ) )
250	249, 62, 27	fovrnd 6806	. . . 4 |- ( ph -> ( G ( 1st ` E ) P ) e. ( Base ` T ) )
251	250, 197	eleqtrrd 2704	. . 3 |- ( ph -> ( G ( 1st ` E ) P ) e. V )
252	219	simprd 479	. . 3 |- ( ph -> ( G M P ) : ( G ( 1st ` Z ) P ) --> ( G ( 1st ` E ) P ) )
253	169, 19, 245, 198, 200, 251, 202, 252	setcco 16733	. 2 |- ( ph -> ( ( G M P ) ( <. ( F ( 1st ` Z ) X ) , ( G ( 1st ` Z ) P ) >. (comp ` T ) ( G ( 1st ` E ) P ) ) ( A ( <. F , X >. ( 2nd ` Z ) <. G , P >. ) K ) ) = ( ( G M P ) o. ( A ( <. F , X >. ( 2nd ` Z ) <. G , P >. ) K ) ) )
254	249, 54, 28	fovrnd 6806	. . . 4 |- ( ph -> ( F ( 1st ` E ) X ) e. ( Base ` T ) )
255	254, 197	eleqtrrd 2704	. . 3 |- ( ph -> ( F ( 1st ` E ) X ) e. V )
256	165, 166, 167, 248, 179, 181	funcf2 16528	. . . . . 6 |- ( ph -> ( <. F , X >. ( 2nd ` E ) <. G , P >. ) : ( <. F , X >. ( Hom ` ( Q X.c O ) ) <. G , P >. ) --> ( ( ( 1st ` E ) ` <. F , X >. ) ( Hom ` T ) ( ( 1st ` E ) ` <. G , P >. ) ) )
257		df-ov 6653	. . . . . . . . . 10 |- ( F ( 1st ` E ) X ) = ( ( 1st ` E ) ` <. F , X >. )
258		df-ov 6653	. . . . . . . . . 10 |- ( G ( 1st ` E ) P ) = ( ( 1st ` E ) ` <. G , P >. )
259	257, 258	oveq12i 6662	. . . . . . . . 9 |- ( ( F ( 1st ` E ) X ) ( Hom ` T ) ( G ( 1st ` E ) P ) ) = ( ( ( 1st ` E ) ` <. F , X >. ) ( Hom ` T ) ( ( 1st ` E ) ` <. G , P >. ) )
260	259	eqcomi 2631	. . . . . . . 8 |- ( ( ( 1st ` E ) ` <. F , X >. ) ( Hom ` T ) ( ( 1st ` E ) ` <. G , P >. ) ) = ( ( F ( 1st ` E ) X ) ( Hom ` T ) ( G ( 1st ` E ) P ) )
261	260	a1i 11	. . . . . . 7 |- ( ph -> ( ( ( 1st ` E ) ` <. F , X >. ) ( Hom ` T ) ( ( 1st ` E ) ` <. G , P >. ) ) = ( ( F ( 1st ` E ) X ) ( Hom ` T ) ( G ( 1st ` E ) P ) ) )
262	185, 261	feq23d 6040	. . . . . 6 |- ( ph -> ( ( <. F , X >. ( 2nd ` E ) <. G , P >. ) : ( <. F , X >. ( Hom ` ( Q X.c O ) ) <. G , P >. ) --> ( ( ( 1st ` E ) ` <. F , X >. ) ( Hom ` T ) ( ( 1st ` E ) ` <. G , P >. ) ) <-> ( <. F , X >. ( 2nd ` E ) <. G , P >. ) : ( ( F ( O Nat S ) G ) X. ( P ( Hom ` C ) X ) ) --> ( ( F ( 1st ` E ) X ) ( Hom ` T ) ( G ( 1st ` E ) P ) ) ) )
263	256, 262	mpbid 222	. . . . 5 |- ( ph -> ( <. F , X >. ( 2nd ` E ) <. G , P >. ) : ( ( F ( O Nat S ) G ) X. ( P ( Hom ` C ) X ) ) --> ( ( F ( 1st ` E ) X ) ( Hom ` T ) ( G ( 1st ` E ) P ) ) )
264	263, 34, 30	fovrnd 6806	. . . 4 |- ( ph -> ( A ( <. F , X >. ( 2nd ` E ) <. G , P >. ) K ) e. ( ( F ( 1st ` E ) X ) ( Hom ` T ) ( G ( 1st ` E ) P ) ) )
265	169, 19, 167, 255, 251	elsetchom 16731	. . . 4 |- ( ph -> ( ( A ( <. F , X >. ( 2nd ` E ) <. G , P >. ) K ) e. ( ( F ( 1st ` E ) X ) ( Hom ` T ) ( G ( 1st ` E ) P ) ) <-> ( A ( <. F , X >. ( 2nd ` E ) <. G , P >. ) K ) : ( F ( 1st ` E ) X ) --> ( G ( 1st ` E ) P ) ) )
266	264, 265	mpbid 222	. . 3 |- ( ph -> ( A ( <. F , X >. ( 2nd ` E ) <. G , P >. ) K ) : ( F ( 1st ` E ) X ) --> ( G ( 1st ` E ) P ) )
267	169, 19, 245, 198, 255, 251, 230, 266	setcco 16733	. 2 |- ( ph -> ( ( A ( <. F , X >. ( 2nd ` E ) <. G , P >. ) K ) ( <. ( F ( 1st ` Z ) X ) , ( F ( 1st ` E ) X ) >. (comp ` T ) ( G ( 1st ` E ) P ) ) ( F M X ) ) = ( ( A ( <. F , X >. ( 2nd ` E ) <. G , P >. ) K ) o. ( F M X ) ) )
268	244, 253, 267	3eqtr4d 2666	1 |- ( ph -> ( ( G M P ) ( <. ( F ( 1st ` Z ) X ) , ( G ( 1st ` Z ) P ) >. (comp ` T ) ( G ( 1st ` E ) P ) ) ( A ( <. F , X >. ( 2nd ` Z ) <. G , P >. ) K ) ) = ( ( A ( <. F , X >. ( 2nd ` E ) <. G , P >. ) K ) ( <. ( F ( 1st ` Z ) X ) , ( F ( 1st ` E ) X ) >. (comp ` T ) ( G ( 1st ` E ) P ) ) ( F M X ) ) )

Syntax hints:   -> wi 4   /\ wa 384   = wceq 1483   e. wcel 1990   A.wral 2912   _Vcvv 3200   u. cun 3572   C_ wss 3574   <.cop 4183   class class class wbr 4653   |-> cmpt 4729   X. cxp 5112   ran crn 5115   o. ccom 5118   Rel wrel 5119   -->wf 5884   ` cfv 5888  (class class class)co 6650   |-> cmpt2 6652   1stc1st 7166   2ndc2nd 7167  tpos ctpos 7351   Basecbs 15857   Hom chom 15952  compcco 15953   Catccat 16325   Idccid 16326   Hom _f chomf 16327  oppCatcoppc 16371   Func cfunc 16514   o._func ccofu 16516   Nat cnat 16601   FuncCat cfuc 16602   SetCatcsetc 16725   X._c cxpc 16808   1st_F c1stf 16809   2nd_F c2ndf 16810   ⟨,⟩_F cprf 16811   eval_F cevlf 16849  Hom_Fchof 16888  Yoncyon 16889

This theorem was proved from axioms:  ax-mp 5  ax-1 6  ax-2 7  ax-3 8  ax-gen 1722  ax-4 1737  ax-5 1839  ax-6 1888  ax-7 1935  ax-8 1992  ax-9 1999  ax-10 2019  ax-11 2034  ax-12 2047  ax-13 2246  ax-ext 2602  ax-rep 4771  ax-sep 4781  ax-nul 4789  ax-pow 4843  ax-pr 4906  ax-un 6949  ax-cnex 9992  ax-resscn 9993  ax-1cn 9994  ax-icn 9995  ax-addcl 9996  ax-addrcl 9997  ax-mulcl 9998  ax-mulrcl 9999  ax-mulcom 10000  ax-addass 10001  ax-mulass 10002  ax-distr 10003  ax-i2m1 10004  ax-1ne0 10005  ax-1rid 10006  ax-rnegex 10007  ax-rrecex 10008  ax-cnre 10009  ax-pre-lttri 10010  ax-pre-lttrn 10011  ax-pre-ltadd 10012  ax-pre-mulgt0 10013

This theorem depends on definitions:  df-bi 197  df-or 385  df-an 386  df-3or 1038  df-3an 1039  df-tru 1486  df-fal 1489  df-ex 1705  df-nf 1710  df-sb 1881  df-eu 2474  df-mo 2475  df-clab 2609  df-cleq 2615  df-clel 2618  df-nfc 2753  df-ne 2795  df-nel 2898  df-ral 2917  df-rex 2918  df-reu 2919  df-rmo 2920  df-rab 2921  df-v 3202  df-sbc 3436  df-csb 3534  df-dif 3577  df-un 3579  df-in 3581  df-ss 3588  df-pss 3590  df-nul 3916  df-if 4087  df-pw 4160  df-sn 4178  df-pr 4180  df-tp 4182  df-op 4184  df-uni 4437  df-int 4476  df-iun 4522  df-br 4654  df-opab 4713  df-mpt 4730  df-tr 4753  df-id 5024  df-eprel 5029  df-po 5035  df-so 5036  df-fr 5073  df-we 5075  df-xp 5120  df-rel 5121  df-cnv 5122  df-co 5123  df-dm 5124  df-rn 5125  df-res 5126  df-ima 5127  df-pred 5680  df-ord 5726  df-on 5727  df-lim 5728  df-suc 5729  df-iota 5851  df-fun 5890  df-fn 5891  df-f 5892  df-f1 5893  df-fo 5894  df-f1o 5895  df-fv 5896  df-riota 6611  df-ov 6653  df-oprab 6654  df-mpt2 6655  df-om 7066  df-1st 7168  df-2nd 7169  df-tpos 7352  df-wrecs 7407  df-recs 7468  df-rdg 7506  df-1o 7560  df-oadd 7564  df-er 7742  df-map 7859  df-pm 7860  df-ixp 7909  df-en 7956  df-dom 7957  df-sdom 7958  df-fin 7959  df-pnf 10076  df-mnf 10077  df-xr 10078  df-ltxr 10079  df-le 10080  df-sub 10268  df-neg 10269  df-nn 11021  df-2 11079  df-3 11080  df-4 11081  df-5 11082  df-6 11083  df-7 11084  df-8 11085  df-9 11086  df-n0 11293  df-z 11378  df-dec 11494  df-uz 11688  df-fz 12327  df-struct 15859  df-ndx 15860  df-slot 15861  df-base 15863  df-sets 15864  df-ress 15865  df-hom 15966  df-cco 15967  df-cat 16329  df-cid 16330  df-homf 16331  df-comf 16332  df-oppc 16372  df-ssc 16470  df-resc 16471  df-subc 16472  df-func 16518  df-cofu 16520  df-nat 16603  df-fuc 16604  df-setc 16726  df-xpc 16812  df-1stf 16813  df-2ndf 16814  df-prf 16815  df-evlf 16853  df-curf 16854  df-hof 16890  df-yon 16891

This theorem is referenced by:  yonedalem3  16920