Theorem yonffthlem 16922

Description: Lemma for yonffth 16924. (Contributed by Mario Carneiro, 29-Jan-2017.)

Hypotheses

Ref	Expression
yoneda.y	|- Y = (Yon ` C )
yoneda.b	|- B = ( Base ` C )
yoneda.1	|- .1. = ( Id ` C )
yoneda.o	|- O = (oppCat ` C )
yoneda.s	|- S = ( SetCat ` U )
yoneda.t	|- T = ( SetCat ` V )
yoneda.q	|- Q = ( O FuncCat S )
yoneda.h	|- H = (HomF ` Q )
yoneda.r	|- R = ( ( Q X.c O ) FuncCat T )
yoneda.e	|- E = ( O evalF S )
yoneda.z	|- Z = ( H o.func ( ( <. ( 1st ` Y ) , tpos ( 2nd ` Y ) >. o.func ( Q 2ndF O ) ) ⟨,⟩F ( Q 1stF O ) ) )
yoneda.c	|- ( ph -> C e. Cat )
yoneda.w	|- ( ph -> V e. W )
yoneda.u	|- ( ph -> ran ( Hom f ` C ) C_ U )
yoneda.v	|- ( ph -> ( ran ( Hom f ` Q ) u. U ) C_ V )
yoneda.m	|- M = ( f e. ( O Func S ) , x e. B |-> ( a e. ( ( ( 1st ` Y ) ` x ) ( O Nat S ) f ) |-> ( ( a ` x ) ` ( .1. ` x ) ) ) )
yonedainv.i	|- I = (Inv ` R )
yonedainv.n	|- N = ( f e. ( O Func S ) , x e. B |-> ( u e. ( ( 1st ` f ) ` x ) |-> ( y e. B |-> ( g e. ( y ( Hom ` C ) x ) |-> ( ( ( x ( 2nd ` f ) y ) ` g ) ` u ) ) ) ) )

Assertion

Ref	Expression
yonffthlem	|- ( ph -> Y e. ( ( C Full Q ) i^i ( C Faith Q ) ) )

Distinct variable groups:   f, a, g, x, y, .1.   u, a, g, y, C, f, x   E, a, f, g, u, y   B, a, f, g, u, x, y   N, a   O, a, f, g, u, x, y   S, a, f, g, u, x, y   g, M, u, y   Q, a, f, g, u, x   T, f, g, u, y   ph, a, f, g, u, x, y   u, R   Y, a, f, g, u, x, y   Z, a, f, g, u, x, y

Allowed substitution hints:   Q( y)   R( x, y, f, g, a)   T( x, a)   U( x, y, u, f, g, a)   .1. ( u)   E( x)   H( x, y, u, f, g, a)   I( x, y, u, f, g, a)   M( x, f, a)   N( x, y, u, f, g)   V( x, y, u, f, g, a)   W( x, y, u, f, g, a)

Proof of Theorem yonffthlem

Dummy variables h w z v are mutually distinct and distinct from all other variables.

Step	Hyp	Ref	Expression
1		relfunc 16522	. . 3 |- Rel ( C Func Q )
2		yoneda.y	. . . 4 |- Y = (Yon ` C )
3		yoneda.c	. . . 4 |- ( ph -> C e. Cat )
4		yoneda.o	. . . 4 |- O = (oppCat ` C )
5		yoneda.s	. . . 4 |- S = ( SetCat ` U )
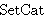6		yoneda.q	. . . 4 |- Q = ( O FuncCat S )
7		yoneda.w	. . . . 5 |- ( ph -> V e. W )
8		yoneda.v	. . . . . 6 |- ( ph -> ( ran ( Hom f ` Q ) u. U ) C_ V )
9	8	unssbd 3791	. . . . 5 |- ( ph -> U C_ V )
10	7, 9	ssexd 4805	. . . 4 |- ( ph -> U e. _V )
11		yoneda.u	. . . 4 |- ( ph -> ran ( Hom f ` C ) C_ U )
12	2, 3, 4, 5, 6, 10, 11	yoncl 16902	. . 3 |- ( ph -> Y e. ( C Func Q ) )
13		1st2nd 7214	. . 3 |- ( ( Rel ( C Func Q ) /\ Y e. ( C Func Q ) ) -> Y = <. ( 1st ` Y ) , ( 2nd ` Y ) >. )
14	1, 12, 13	sylancr 695	. 2 |- ( ph -> Y = <. ( 1st ` Y ) , ( 2nd ` Y ) >. )
15		1st2ndbr 7217	. . . . 5 |- ( ( Rel ( C Func Q ) /\ Y e. ( C Func Q ) ) -> ( 1st ` Y ) ( C Func Q ) ( 2nd ` Y ) )
16	1, 12, 15	sylancr 695	. . . 4 |- ( ph -> ( 1st ` Y ) ( C Func Q ) ( 2nd ` Y ) )
17		yoneda.b	. . . . . . . . . . . . 13 |- B = ( Base ` C )
18	6	fucbas 16620	. . . . . . . . . . . . 13 |- ( O Func S ) = ( Base ` Q )
19	17, 18, 16	funcf1 16526	. . . . . . . . . . . 12 |- ( ph -> ( 1st ` Y ) : B --> ( O Func S ) )
20	19	adantr 481	. . . . . . . . . . 11 |- ( ( ph /\ ( z e. B /\ w e. B ) ) -> ( 1st ` Y ) : B --> ( O Func S ) )
21		simprr 796	. . . . . . . . . . 11 |- ( ( ph /\ ( z e. B /\ w e. B ) ) -> w e. B )
22	20, 21	ffvelrnd 6360	. . . . . . . . . 10 |- ( ( ph /\ ( z e. B /\ w e. B ) ) -> ( ( 1st ` Y ) ` w ) e. ( O Func S ) )
23		simprl 794	. . . . . . . . . 10 |- ( ( ph /\ ( z e. B /\ w e. B ) ) -> z e. B )
24		opelxpi 5148	. . . . . . . . . 10 |- ( ( ( ( 1st ` Y ) ` w ) e. ( O Func S ) /\ z e. B ) -> <. ( ( 1st ` Y ) ` w ) , z >. e. ( ( O Func S ) X. B ) )
25	22, 23, 24	syl2anc 693	. . . . . . . . 9 |- ( ( ph /\ ( z e. B /\ w e. B ) ) -> <. ( ( 1st ` Y ) ` w ) , z >. e. ( ( O Func S ) X. B ) )
26		yoneda.r	. . . . . . . . . . . . . 14 |- R = ( ( Q X.c O ) FuncCat T )
27	26	fucbas 16620	. . . . . . . . . . . . 13 |- ( ( Q X.c O ) Func T ) = ( Base ` R )
28		yonedainv.i	. . . . . . . . . . . . 13 |- I = (Inv ` R )
29		yoneda.1	. . . . . . . . . . . . . . . . . 18 |- .1. = ( Id ` C )
30		yoneda.t	. . . . . . . . . . . . . . . . . 18 |- T = ( SetCat ` V )
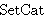31		yoneda.h	. . . . . . . . . . . . . . . . . 18 |- H = (HomF ` Q )
32		yoneda.e	. . . . . . . . . . . . . . . . . 18 |- E = ( O evalF S )
33		yoneda.z	. . . . . . . . . . . . . . . . . 18 |- Z = ( H o.func ( ( <. ( 1st ` Y ) , tpos ( 2nd ` Y ) >. o.func ( Q 2ndF O ) ) ⟨,⟩F ( Q 1stF O ) ) )
34	2, 17, 29, 4, 5, 30, 6, 31, 26, 32, 33, 3, 7, 11, 8	yonedalem1 16912	. . . . . . . . . . . . . . . . 17 |- ( ph -> ( Z e. ( ( Q X.c O ) Func T ) /\ E e. ( ( Q X.c O ) Func T ) ) )
35	34	simpld 475	. . . . . . . . . . . . . . . 16 |- ( ph -> Z e. ( ( Q X.c O ) Func T ) )
36		funcrcl 16523	. . . . . . . . . . . . . . . 16 |- ( Z e. ( ( Q X.c O ) Func T ) -> ( ( Q X.c O ) e. Cat /\ T e. Cat ) )
37	35, 36	syl 17	. . . . . . . . . . . . . . 15 |- ( ph -> ( ( Q X.c O ) e. Cat /\ T e. Cat ) )
38	37	simpld 475	. . . . . . . . . . . . . 14 |- ( ph -> ( Q X.c O ) e. Cat )
39	37	simprd 479	. . . . . . . . . . . . . 14 |- ( ph -> T e. Cat )
40	26, 38, 39	fuccat 16630	. . . . . . . . . . . . 13 |- ( ph -> R e. Cat )
41	34	simprd 479	. . . . . . . . . . . . 13 |- ( ph -> E e. ( ( Q X.c O ) Func T ) )
42		eqid 2622	. . . . . . . . . . . . 13 |- ( Iso ` R ) = ( Iso ` R )
43		yoneda.m	. . . . . . . . . . . . . 14 |- M = ( f e. ( O Func S ) , x e. B |-> ( a e. ( ( ( 1st ` Y ) ` x ) ( O Nat S ) f ) |-> ( ( a ` x ) ` ( .1. ` x ) ) ) )
44		yonedainv.n	. . . . . . . . . . . . . 14 |- N = ( f e. ( O Func S ) , x e. B |-> ( u e. ( ( 1st ` f ) ` x ) |-> ( y e. B |-> ( g e. ( y ( Hom ` C ) x ) |-> ( ( ( x ( 2nd ` f ) y ) ` g ) ` u ) ) ) ) )
45	2, 17, 29, 4, 5, 30, 6, 31, 26, 32, 33, 3, 7, 11, 8, 43, 28, 44	yonedainv 16921	. . . . . . . . . . . . 13 |- ( ph -> M ( Z I E ) N )
46	27, 28, 40, 35, 41, 42, 45	inviso2 16427	. . . . . . . . . . . 12 |- ( ph -> N e. ( E ( Iso ` R ) Z ) )
47		eqid 2622	. . . . . . . . . . . . . 14 |- ( Q X.c O ) = ( Q X.c O )
48	4, 17	oppcbas 16378	. . . . . . . . . . . . . 14 |- B = ( Base ` O )
49	47, 18, 48	xpcbas 16818	. . . . . . . . . . . . 13 |- ( ( O Func S ) X. B ) = ( Base ` ( Q X.c O ) )
50		eqid 2622	. . . . . . . . . . . . 13 |- ( ( Q X.c O ) Nat T ) = ( ( Q X.c O ) Nat T )
51		eqid 2622	. . . . . . . . . . . . 13 |- ( Iso ` T ) = ( Iso ` T )
52	26, 49, 50, 41, 35, 42, 51	fuciso 16635	. . . . . . . . . . . 12 |- ( ph -> ( N e. ( E ( Iso ` R ) Z ) <-> ( N e. ( E ( ( Q X.c O ) Nat T ) Z ) /\ A. v e. ( ( O Func S ) X. B ) ( N ` v ) e. ( ( ( 1st ` E ) ` v ) ( Iso ` T ) ( ( 1st ` Z ) ` v ) ) ) ) )
53	46, 52	mpbid 222	. . . . . . . . . . 11 |- ( ph -> ( N e. ( E ( ( Q X.c O ) Nat T ) Z ) /\ A. v e. ( ( O Func S ) X. B ) ( N ` v ) e. ( ( ( 1st ` E ) ` v ) ( Iso ` T ) ( ( 1st ` Z ) ` v ) ) ) )
54	53	simprd 479	. . . . . . . . . 10 |- ( ph -> A. v e. ( ( O Func S ) X. B ) ( N ` v ) e. ( ( ( 1st ` E ) ` v ) ( Iso ` T ) ( ( 1st ` Z ) ` v ) ) )
55	54	adantr 481	. . . . . . . . 9 |- ( ( ph /\ ( z e. B /\ w e. B ) ) -> A. v e. ( ( O Func S ) X. B ) ( N ` v ) e. ( ( ( 1st ` E ) ` v ) ( Iso ` T ) ( ( 1st ` Z ) ` v ) ) )
56		fveq2 6191	. . . . . . . . . . . 12 |- ( v = <. ( ( 1st ` Y ) ` w ) , z >. -> ( N ` v ) = ( N ` <. ( ( 1st ` Y ) ` w ) , z >. ) )
57		df-ov 6653	. . . . . . . . . . . 12 |- ( ( ( 1st ` Y ) ` w ) N z ) = ( N ` <. ( ( 1st ` Y ) ` w ) , z >. )
58	56, 57	syl6eqr 2674	. . . . . . . . . . 11 |- ( v = <. ( ( 1st ` Y ) ` w ) , z >. -> ( N ` v ) = ( ( ( 1st ` Y ) ` w ) N z ) )
59		fveq2 6191	. . . . . . . . . . . . 13 |- ( v = <. ( ( 1st ` Y ) ` w ) , z >. -> ( ( 1st ` E ) ` v ) = ( ( 1st ` E ) ` <. ( ( 1st ` Y ) ` w ) , z >. ) )
60		df-ov 6653	. . . . . . . . . . . . 13 |- ( ( ( 1st ` Y ) ` w ) ( 1st ` E ) z ) = ( ( 1st ` E ) ` <. ( ( 1st ` Y ) ` w ) , z >. )
61	59, 60	syl6eqr 2674	. . . . . . . . . . . 12 |- ( v = <. ( ( 1st ` Y ) ` w ) , z >. -> ( ( 1st ` E ) ` v ) = ( ( ( 1st ` Y ) ` w ) ( 1st ` E ) z ) )
62		fveq2 6191	. . . . . . . . . . . . 13 |- ( v = <. ( ( 1st ` Y ) ` w ) , z >. -> ( ( 1st ` Z ) ` v ) = ( ( 1st ` Z ) ` <. ( ( 1st ` Y ) ` w ) , z >. ) )
63		df-ov 6653	. . . . . . . . . . . . 13 |- ( ( ( 1st ` Y ) ` w ) ( 1st ` Z ) z ) = ( ( 1st ` Z ) ` <. ( ( 1st ` Y ) ` w ) , z >. )
64	62, 63	syl6eqr 2674	. . . . . . . . . . . 12 |- ( v = <. ( ( 1st ` Y ) ` w ) , z >. -> ( ( 1st ` Z ) ` v ) = ( ( ( 1st ` Y ) ` w ) ( 1st ` Z ) z ) )
65	61, 64	oveq12d 6668	. . . . . . . . . . 11 |- ( v = <. ( ( 1st ` Y ) ` w ) , z >. -> ( ( ( 1st ` E ) ` v ) ( Iso ` T ) ( ( 1st ` Z ) ` v ) ) = ( ( ( ( 1st ` Y ) ` w ) ( 1st ` E ) z ) ( Iso ` T ) ( ( ( 1st ` Y ) ` w ) ( 1st ` Z ) z ) ) )
66	58, 65	eleq12d 2695	. . . . . . . . . 10 |- ( v = <. ( ( 1st ` Y ) ` w ) , z >. -> ( ( N ` v ) e. ( ( ( 1st ` E ) ` v ) ( Iso ` T ) ( ( 1st ` Z ) ` v ) ) <-> ( ( ( 1st ` Y ) ` w ) N z ) e. ( ( ( ( 1st ` Y ) ` w ) ( 1st ` E ) z ) ( Iso ` T ) ( ( ( 1st ` Y ) ` w ) ( 1st ` Z ) z ) ) ) )
67	66	rspcv 3305	. . . . . . . . 9 |- ( <. ( ( 1st ` Y ) ` w ) , z >. e. ( ( O Func S ) X. B ) -> ( A. v e. ( ( O Func S ) X. B ) ( N ` v ) e. ( ( ( 1st ` E ) ` v ) ( Iso ` T ) ( ( 1st ` Z ) ` v ) ) -> ( ( ( 1st ` Y ) ` w ) N z ) e. ( ( ( ( 1st ` Y ) ` w ) ( 1st ` E ) z ) ( Iso ` T ) ( ( ( 1st ` Y ) ` w ) ( 1st ` Z ) z ) ) ) )
68	25, 55, 67	sylc 65	. . . . . . . 8 |- ( ( ph /\ ( z e. B /\ w e. B ) ) -> ( ( ( 1st ` Y ) ` w ) N z ) e. ( ( ( ( 1st ` Y ) ` w ) ( 1st ` E ) z ) ( Iso ` T ) ( ( ( 1st ` Y ) ` w ) ( 1st ` Z ) z ) ) )
69	4	oppccat 16382	. . . . . . . . . . . . 13 |- ( C e. Cat -> O e. Cat )
70	3, 69	syl 17	. . . . . . . . . . . 12 |- ( ph -> O e. Cat )
71	70	adantr 481	. . . . . . . . . . 11 |- ( ( ph /\ ( z e. B /\ w e. B ) ) -> O e. Cat )
72	5	setccat 16735	. . . . . . . . . . . . 13 |- ( U e. _V -> S e. Cat )
73	10, 72	syl 17	. . . . . . . . . . . 12 |- ( ph -> S e. Cat )
74	73	adantr 481	. . . . . . . . . . 11 |- ( ( ph /\ ( z e. B /\ w e. B ) ) -> S e. Cat )
75	32, 71, 74, 48, 22, 23	evlf1 16860	. . . . . . . . . 10 |- ( ( ph /\ ( z e. B /\ w e. B ) ) -> ( ( ( 1st ` Y ) ` w ) ( 1st ` E ) z ) = ( ( 1st ` ( ( 1st ` Y ) ` w ) ) ` z ) )
76	3	adantr 481	. . . . . . . . . . 11 |- ( ( ph /\ ( z e. B /\ w e. B ) ) -> C e. Cat )
77		eqid 2622	. . . . . . . . . . 11 |- ( Hom ` C ) = ( Hom ` C )
78	2, 17, 76, 21, 77, 23	yon11 16904	. . . . . . . . . 10 |- ( ( ph /\ ( z e. B /\ w e. B ) ) -> ( ( 1st ` ( ( 1st ` Y ) ` w ) ) ` z ) = ( z ( Hom ` C ) w ) )
79	75, 78	eqtrd 2656	. . . . . . . . 9 |- ( ( ph /\ ( z e. B /\ w e. B ) ) -> ( ( ( 1st ` Y ) ` w ) ( 1st ` E ) z ) = ( z ( Hom ` C ) w ) )
80	7	adantr 481	. . . . . . . . . 10 |- ( ( ph /\ ( z e. B /\ w e. B ) ) -> V e. W )
81	11	adantr 481	. . . . . . . . . 10 |- ( ( ph /\ ( z e. B /\ w e. B ) ) -> ran ( Hom f ` C ) C_ U )
82	8	adantr 481	. . . . . . . . . 10 |- ( ( ph /\ ( z e. B /\ w e. B ) ) -> ( ran ( Hom f ` Q ) u. U ) C_ V )
83	2, 17, 29, 4, 5, 30, 6, 31, 26, 32, 33, 76, 80, 81, 82, 22, 23	yonedalem21 16913	. . . . . . . . 9 |- ( ( ph /\ ( z e. B /\ w e. B ) ) -> ( ( ( 1st ` Y ) ` w ) ( 1st ` Z ) z ) = ( ( ( 1st ` Y ) ` z ) ( O Nat S ) ( ( 1st ` Y ) ` w ) ) )
84	79, 83	oveq12d 6668	. . . . . . . 8 |- ( ( ph /\ ( z e. B /\ w e. B ) ) -> ( ( ( ( 1st ` Y ) ` w ) ( 1st ` E ) z ) ( Iso ` T ) ( ( ( 1st ` Y ) ` w ) ( 1st ` Z ) z ) ) = ( ( z ( Hom ` C ) w ) ( Iso ` T ) ( ( ( 1st ` Y ) ` z ) ( O Nat S ) ( ( 1st ` Y ) ` w ) ) ) )
85	68, 84	eleqtrd 2703	. . . . . . 7 |- ( ( ph /\ ( z e. B /\ w e. B ) ) -> ( ( ( 1st ` Y ) ` w ) N z ) e. ( ( z ( Hom ` C ) w ) ( Iso ` T ) ( ( ( 1st ` Y ) ` z ) ( O Nat S ) ( ( 1st ` Y ) ` w ) ) ) )
86	9	adantr 481	. . . . . . . . 9 |- ( ( ph /\ ( z e. B /\ w e. B ) ) -> U C_ V )
87		eqid 2622	. . . . . . . . . . . . 13 |- ( Base ` S ) = ( Base ` S )
88		relfunc 16522	. . . . . . . . . . . . . 14 |- Rel ( O Func S )
89		1st2ndbr 7217	. . . . . . . . . . . . . 14 |- ( ( Rel ( O Func S ) /\ ( ( 1st ` Y ) ` w ) e. ( O Func S ) ) -> ( 1st ` ( ( 1st ` Y ) ` w ) ) ( O Func S ) ( 2nd ` ( ( 1st ` Y ) ` w ) ) )
90	88, 22, 89	sylancr 695	. . . . . . . . . . . . 13 |- ( ( ph /\ ( z e. B /\ w e. B ) ) -> ( 1st ` ( ( 1st ` Y ) ` w ) ) ( O Func S ) ( 2nd ` ( ( 1st ` Y ) ` w ) ) )
91	48, 87, 90	funcf1 16526	. . . . . . . . . . . 12 |- ( ( ph /\ ( z e. B /\ w e. B ) ) -> ( 1st ` ( ( 1st ` Y ) ` w ) ) : B --> ( Base ` S ) )
92	91, 23	ffvelrnd 6360	. . . . . . . . . . 11 |- ( ( ph /\ ( z e. B /\ w e. B ) ) -> ( ( 1st ` ( ( 1st ` Y ) ` w ) ) ` z ) e. ( Base ` S ) )
93	5, 10	setcbas 16728	. . . . . . . . . . . 12 |- ( ph -> U = ( Base ` S ) )
94	93	adantr 481	. . . . . . . . . . 11 |- ( ( ph /\ ( z e. B /\ w e. B ) ) -> U = ( Base ` S ) )
95	92, 94	eleqtrrd 2704	. . . . . . . . . 10 |- ( ( ph /\ ( z e. B /\ w e. B ) ) -> ( ( 1st ` ( ( 1st ` Y ) ` w ) ) ` z ) e. U )
96	78, 95	eqeltrrd 2702	. . . . . . . . 9 |- ( ( ph /\ ( z e. B /\ w e. B ) ) -> ( z ( Hom ` C ) w ) e. U )
97	86, 96	sseldd 3604	. . . . . . . 8 |- ( ( ph /\ ( z e. B /\ w e. B ) ) -> ( z ( Hom ` C ) w ) e. V )
98		eqid 2622	. . . . . . . . . 10 |- ( Hom f ` Q ) = ( Hom f ` Q )
99		eqid 2622	. . . . . . . . . . 11 |- ( O Nat S ) = ( O Nat S )
100	6, 99	fuchom 16621	. . . . . . . . . 10 |- ( O Nat S ) = ( Hom ` Q )
101	20, 23	ffvelrnd 6360	. . . . . . . . . 10 |- ( ( ph /\ ( z e. B /\ w e. B ) ) -> ( ( 1st ` Y ) ` z ) e. ( O Func S ) )
102	98, 18, 100, 101, 22	homfval 16352	. . . . . . . . 9 |- ( ( ph /\ ( z e. B /\ w e. B ) ) -> ( ( ( 1st ` Y ) ` z ) ( Hom f ` Q ) ( ( 1st ` Y ) ` w ) ) = ( ( ( 1st ` Y ) ` z ) ( O Nat S ) ( ( 1st ` Y ) ` w ) ) )
103	8	unssad 3790	. . . . . . . . . . 11 |- ( ph -> ran ( Hom f ` Q ) C_ V )
104	103	adantr 481	. . . . . . . . . 10 |- ( ( ph /\ ( z e. B /\ w e. B ) ) -> ran ( Hom f ` Q ) C_ V )
105	98, 18	homffn 16353	. . . . . . . . . . . 12 |- ( Hom f ` Q ) Fn ( ( O Func S ) X. ( O Func S ) )
106	105	a1i 11	. . . . . . . . . . 11 |- ( ( ph /\ ( z e. B /\ w e. B ) ) -> ( Hom f ` Q ) Fn ( ( O Func S ) X. ( O Func S ) ) )
107		fnovrn 6809	. . . . . . . . . . 11 |- ( ( ( Hom f ` Q ) Fn ( ( O Func S ) X. ( O Func S ) ) /\ ( ( 1st ` Y ) ` z ) e. ( O Func S ) /\ ( ( 1st ` Y ) ` w ) e. ( O Func S ) ) -> ( ( ( 1st ` Y ) ` z ) ( Hom f ` Q ) ( ( 1st ` Y ) ` w ) ) e. ran ( Hom f ` Q ) )
108	106, 101, 22, 107	syl3anc 1326	. . . . . . . . . 10 |- ( ( ph /\ ( z e. B /\ w e. B ) ) -> ( ( ( 1st ` Y ) ` z ) ( Hom f ` Q ) ( ( 1st ` Y ) ` w ) ) e. ran ( Hom f ` Q ) )
109	104, 108	sseldd 3604	. . . . . . . . 9 |- ( ( ph /\ ( z e. B /\ w e. B ) ) -> ( ( ( 1st ` Y ) ` z ) ( Hom f ` Q ) ( ( 1st ` Y ) ` w ) ) e. V )
110	102, 109	eqeltrrd 2702	. . . . . . . 8 |- ( ( ph /\ ( z e. B /\ w e. B ) ) -> ( ( ( 1st ` Y ) ` z ) ( O Nat S ) ( ( 1st ` Y ) ` w ) ) e. V )
111	30, 80, 97, 110, 51	setciso 16741	. . . . . . 7 |- ( ( ph /\ ( z e. B /\ w e. B ) ) -> ( ( ( ( 1st ` Y ) ` w ) N z ) e. ( ( z ( Hom ` C ) w ) ( Iso ` T ) ( ( ( 1st ` Y ) ` z ) ( O Nat S ) ( ( 1st ` Y ) ` w ) ) ) <-> ( ( ( 1st ` Y ) ` w ) N z ) : ( z ( Hom ` C ) w ) -1-1-onto-> ( ( ( 1st ` Y ) ` z ) ( O Nat S ) ( ( 1st ` Y ) ` w ) ) ) )
112	85, 111	mpbid 222	. . . . . 6 |- ( ( ph /\ ( z e. B /\ w e. B ) ) -> ( ( ( 1st ` Y ) ` w ) N z ) : ( z ( Hom ` C ) w ) -1-1-onto-> ( ( ( 1st ` Y ) ` z ) ( O Nat S ) ( ( 1st ` Y ) ` w ) ) )
113	76	adantr 481	. . . . . . . . . . . . . . . 16 |- ( ( ( ph /\ ( z e. B /\ w e. B ) ) /\ h e. ( z ( Hom ` C ) w ) ) -> C e. Cat )
114	113	adantr 481	. . . . . . . . . . . . . . 15 |- ( ( ( ( ph /\ ( z e. B /\ w e. B ) ) /\ h e. ( z ( Hom ` C ) w ) ) /\ y e. B ) -> C e. Cat )
115	23	adantr 481	. . . . . . . . . . . . . . . 16 |- ( ( ( ph /\ ( z e. B /\ w e. B ) ) /\ h e. ( z ( Hom ` C ) w ) ) -> z e. B )
116	115	adantr 481	. . . . . . . . . . . . . . 15 |- ( ( ( ( ph /\ ( z e. B /\ w e. B ) ) /\ h e. ( z ( Hom ` C ) w ) ) /\ y e. B ) -> z e. B )
117		simpr 477	. . . . . . . . . . . . . . 15 |- ( ( ( ( ph /\ ( z e. B /\ w e. B ) ) /\ h e. ( z ( Hom ` C ) w ) ) /\ y e. B ) -> y e. B )
118	2, 17, 114, 116, 77, 117	yon11 16904	. . . . . . . . . . . . . 14 |- ( ( ( ( ph /\ ( z e. B /\ w e. B ) ) /\ h e. ( z ( Hom ` C ) w ) ) /\ y e. B ) -> ( ( 1st ` ( ( 1st ` Y ) ` z ) ) ` y ) = ( y ( Hom ` C ) z ) )
119	118	eqcomd 2628	. . . . . . . . . . . . 13 |- ( ( ( ( ph /\ ( z e. B /\ w e. B ) ) /\ h e. ( z ( Hom ` C ) w ) ) /\ y e. B ) -> ( y ( Hom ` C ) z ) = ( ( 1st ` ( ( 1st ` Y ) ` z ) ) ` y ) )
120	114	adantr 481	. . . . . . . . . . . . . . 15 |- ( ( ( ( ( ph /\ ( z e. B /\ w e. B ) ) /\ h e. ( z ( Hom ` C ) w ) ) /\ y e. B ) /\ g e. ( y ( Hom ` C ) z ) ) -> C e. Cat )
121	21	ad3antrrr 766	. . . . . . . . . . . . . . 15 |- ( ( ( ( ( ph /\ ( z e. B /\ w e. B ) ) /\ h e. ( z ( Hom ` C ) w ) ) /\ y e. B ) /\ g e. ( y ( Hom ` C ) z ) ) -> w e. B )
122	116	adantr 481	. . . . . . . . . . . . . . 15 |- ( ( ( ( ( ph /\ ( z e. B /\ w e. B ) ) /\ h e. ( z ( Hom ` C ) w ) ) /\ y e. B ) /\ g e. ( y ( Hom ` C ) z ) ) -> z e. B )
123		eqid 2622	. . . . . . . . . . . . . . 15 |- (comp ` C ) = (comp ` C )
124	117	adantr 481	. . . . . . . . . . . . . . 15 |- ( ( ( ( ( ph /\ ( z e. B /\ w e. B ) ) /\ h e. ( z ( Hom ` C ) w ) ) /\ y e. B ) /\ g e. ( y ( Hom ` C ) z ) ) -> y e. B )
125		simpr 477	. . . . . . . . . . . . . . 15 |- ( ( ( ( ( ph /\ ( z e. B /\ w e. B ) ) /\ h e. ( z ( Hom ` C ) w ) ) /\ y e. B ) /\ g e. ( y ( Hom ` C ) z ) ) -> g e. ( y ( Hom ` C ) z ) )
126		simpllr 799	. . . . . . . . . . . . . . 15 |- ( ( ( ( ( ph /\ ( z e. B /\ w e. B ) ) /\ h e. ( z ( Hom ` C ) w ) ) /\ y e. B ) /\ g e. ( y ( Hom ` C ) z ) ) -> h e. ( z ( Hom ` C ) w ) )
127	2, 17, 120, 121, 77, 122, 123, 124, 125, 126	yon12 16905	. . . . . . . . . . . . . 14 |- ( ( ( ( ( ph /\ ( z e. B /\ w e. B ) ) /\ h e. ( z ( Hom ` C ) w ) ) /\ y e. B ) /\ g e. ( y ( Hom ` C ) z ) ) -> ( ( ( z ( 2nd ` ( ( 1st ` Y ) ` w ) ) y ) ` g ) ` h ) = ( h ( <. y , z >. (comp ` C ) w ) g ) )
128	2, 17, 120, 122, 77, 121, 123, 124, 126, 125	yon2 16906	. . . . . . . . . . . . . 14 |- ( ( ( ( ( ph /\ ( z e. B /\ w e. B ) ) /\ h e. ( z ( Hom ` C ) w ) ) /\ y e. B ) /\ g e. ( y ( Hom ` C ) z ) ) -> ( ( ( ( z ( 2nd ` Y ) w ) ` h ) ` y ) ` g ) = ( h ( <. y , z >. (comp ` C ) w ) g ) )
129	127, 128	eqtr4d 2659	. . . . . . . . . . . . 13 |- ( ( ( ( ( ph /\ ( z e. B /\ w e. B ) ) /\ h e. ( z ( Hom ` C ) w ) ) /\ y e. B ) /\ g e. ( y ( Hom ` C ) z ) ) -> ( ( ( z ( 2nd ` ( ( 1st ` Y ) ` w ) ) y ) ` g ) ` h ) = ( ( ( ( z ( 2nd ` Y ) w ) ` h ) ` y ) ` g ) )
130	119, 129	mpteq12dva 4732	. . . . . . . . . . . 12 |- ( ( ( ( ph /\ ( z e. B /\ w e. B ) ) /\ h e. ( z ( Hom ` C ) w ) ) /\ y e. B ) -> ( g e. ( y ( Hom ` C ) z ) |-> ( ( ( z ( 2nd ` ( ( 1st ` Y ) ` w ) ) y ) ` g ) ` h ) ) = ( g e. ( ( 1st ` ( ( 1st ` Y ) ` z ) ) ` y ) |-> ( ( ( ( z ( 2nd ` Y ) w ) ` h ) ` y ) ` g ) ) )
131	16	adantr 481	. . . . . . . . . . . . . . . . . . 19 |- ( ( ph /\ ( z e. B /\ w e. B ) ) -> ( 1st ` Y ) ( C Func Q ) ( 2nd ` Y ) )
132	17, 77, 100, 131, 23, 21	funcf2 16528	. . . . . . . . . . . . . . . . . 18 |- ( ( ph /\ ( z e. B /\ w e. B ) ) -> ( z ( 2nd ` Y ) w ) : ( z ( Hom ` C ) w ) --> ( ( ( 1st ` Y ) ` z ) ( O Nat S ) ( ( 1st ` Y ) ` w ) ) )
133	132	ffvelrnda 6359	. . . . . . . . . . . . . . . . 17 |- ( ( ( ph /\ ( z e. B /\ w e. B ) ) /\ h e. ( z ( Hom ` C ) w ) ) -> ( ( z ( 2nd ` Y ) w ) ` h ) e. ( ( ( 1st ` Y ) ` z ) ( O Nat S ) ( ( 1st ` Y ) ` w ) ) )
134	99, 133	nat1st2nd 16611	. . . . . . . . . . . . . . . 16 |- ( ( ( ph /\ ( z e. B /\ w e. B ) ) /\ h e. ( z ( Hom ` C ) w ) ) -> ( ( z ( 2nd ` Y ) w ) ` h ) e. ( <. ( 1st ` ( ( 1st ` Y ) ` z ) ) , ( 2nd ` ( ( 1st ` Y ) ` z ) ) >. ( O Nat S ) <. ( 1st ` ( ( 1st ` Y ) ` w ) ) , ( 2nd ` ( ( 1st ` Y ) ` w ) ) >. ) )
135	134	adantr 481	. . . . . . . . . . . . . . 15 |- ( ( ( ( ph /\ ( z e. B /\ w e. B ) ) /\ h e. ( z ( Hom ` C ) w ) ) /\ y e. B ) -> ( ( z ( 2nd ` Y ) w ) ` h ) e. ( <. ( 1st ` ( ( 1st ` Y ) ` z ) ) , ( 2nd ` ( ( 1st ` Y ) ` z ) ) >. ( O Nat S ) <. ( 1st ` ( ( 1st ` Y ) ` w ) ) , ( 2nd ` ( ( 1st ` Y ) ` w ) ) >. ) )
136		eqid 2622	. . . . . . . . . . . . . . 15 |- ( Hom ` S ) = ( Hom ` S )
137	99, 135, 48, 136, 117	natcl 16613	. . . . . . . . . . . . . 14 |- ( ( ( ( ph /\ ( z e. B /\ w e. B ) ) /\ h e. ( z ( Hom ` C ) w ) ) /\ y e. B ) -> ( ( ( z ( 2nd ` Y ) w ) ` h ) ` y ) e. ( ( ( 1st ` ( ( 1st ` Y ) ` z ) ) ` y ) ( Hom ` S ) ( ( 1st ` ( ( 1st ` Y ) ` w ) ) ` y ) ) )
138	10	adantr 481	. . . . . . . . . . . . . . . 16 |- ( ( ph /\ ( z e. B /\ w e. B ) ) -> U e. _V )
139	138	ad2antrr 762	. . . . . . . . . . . . . . 15 |- ( ( ( ( ph /\ ( z e. B /\ w e. B ) ) /\ h e. ( z ( Hom ` C ) w ) ) /\ y e. B ) -> U e. _V )
140	19	ad2antrr 762	. . . . . . . . . . . . . . . . . . . 20 |- ( ( ( ph /\ ( z e. B /\ w e. B ) ) /\ h e. ( z ( Hom ` C ) w ) ) -> ( 1st ` Y ) : B --> ( O Func S ) )
141	140, 115	ffvelrnd 6360	. . . . . . . . . . . . . . . . . . 19 |- ( ( ( ph /\ ( z e. B /\ w e. B ) ) /\ h e. ( z ( Hom ` C ) w ) ) -> ( ( 1st ` Y ) ` z ) e. ( O Func S ) )
142		1st2ndbr 7217	. . . . . . . . . . . . . . . . . . 19 |- ( ( Rel ( O Func S ) /\ ( ( 1st ` Y ) ` z ) e. ( O Func S ) ) -> ( 1st ` ( ( 1st ` Y ) ` z ) ) ( O Func S ) ( 2nd ` ( ( 1st ` Y ) ` z ) ) )
143	88, 141, 142	sylancr 695	. . . . . . . . . . . . . . . . . 18 |- ( ( ( ph /\ ( z e. B /\ w e. B ) ) /\ h e. ( z ( Hom ` C ) w ) ) -> ( 1st ` ( ( 1st ` Y ) ` z ) ) ( O Func S ) ( 2nd ` ( ( 1st ` Y ) ` z ) ) )
144	48, 87, 143	funcf1 16526	. . . . . . . . . . . . . . . . 17 |- ( ( ( ph /\ ( z e. B /\ w e. B ) ) /\ h e. ( z ( Hom ` C ) w ) ) -> ( 1st ` ( ( 1st ` Y ) ` z ) ) : B --> ( Base ` S ) )
145	144	ffvelrnda 6359	. . . . . . . . . . . . . . . 16 |- ( ( ( ( ph /\ ( z e. B /\ w e. B ) ) /\ h e. ( z ( Hom ` C ) w ) ) /\ y e. B ) -> ( ( 1st ` ( ( 1st ` Y ) ` z ) ) ` y ) e. ( Base ` S ) )
146	94	ad2antrr 762	. . . . . . . . . . . . . . . 16 |- ( ( ( ( ph /\ ( z e. B /\ w e. B ) ) /\ h e. ( z ( Hom ` C ) w ) ) /\ y e. B ) -> U = ( Base ` S ) )
147	145, 146	eleqtrrd 2704	. . . . . . . . . . . . . . 15 |- ( ( ( ( ph /\ ( z e. B /\ w e. B ) ) /\ h e. ( z ( Hom ` C ) w ) ) /\ y e. B ) -> ( ( 1st ` ( ( 1st ` Y ) ` z ) ) ` y ) e. U )
148	91	adantr 481	. . . . . . . . . . . . . . . . 17 |- ( ( ( ph /\ ( z e. B /\ w e. B ) ) /\ h e. ( z ( Hom ` C ) w ) ) -> ( 1st ` ( ( 1st ` Y ) ` w ) ) : B --> ( Base ` S ) )
149	148	ffvelrnda 6359	. . . . . . . . . . . . . . . 16 |- ( ( ( ( ph /\ ( z e. B /\ w e. B ) ) /\ h e. ( z ( Hom ` C ) w ) ) /\ y e. B ) -> ( ( 1st ` ( ( 1st ` Y ) ` w ) ) ` y ) e. ( Base ` S ) )
150	149, 146	eleqtrrd 2704	. . . . . . . . . . . . . . 15 |- ( ( ( ( ph /\ ( z e. B /\ w e. B ) ) /\ h e. ( z ( Hom ` C ) w ) ) /\ y e. B ) -> ( ( 1st ` ( ( 1st ` Y ) ` w ) ) ` y ) e. U )
151	5, 139, 136, 147, 150	elsetchom 16731	. . . . . . . . . . . . . 14 |- ( ( ( ( ph /\ ( z e. B /\ w e. B ) ) /\ h e. ( z ( Hom ` C ) w ) ) /\ y e. B ) -> ( ( ( ( z ( 2nd ` Y ) w ) ` h ) ` y ) e. ( ( ( 1st ` ( ( 1st ` Y ) ` z ) ) ` y ) ( Hom ` S ) ( ( 1st ` ( ( 1st ` Y ) ` w ) ) ` y ) ) <-> ( ( ( z ( 2nd ` Y ) w ) ` h ) ` y ) : ( ( 1st ` ( ( 1st ` Y ) ` z ) ) ` y ) --> ( ( 1st ` ( ( 1st ` Y ) ` w ) ) ` y ) ) )
152	137, 151	mpbid 222	. . . . . . . . . . . . 13 |- ( ( ( ( ph /\ ( z e. B /\ w e. B ) ) /\ h e. ( z ( Hom ` C ) w ) ) /\ y e. B ) -> ( ( ( z ( 2nd ` Y ) w ) ` h ) ` y ) : ( ( 1st ` ( ( 1st ` Y ) ` z ) ) ` y ) --> ( ( 1st ` ( ( 1st ` Y ) ` w ) ) ` y ) )
153	152	feqmptd 6249	. . . . . . . . . . . 12 |- ( ( ( ( ph /\ ( z e. B /\ w e. B ) ) /\ h e. ( z ( Hom ` C ) w ) ) /\ y e. B ) -> ( ( ( z ( 2nd ` Y ) w ) ` h ) ` y ) = ( g e. ( ( 1st ` ( ( 1st ` Y ) ` z ) ) ` y ) |-> ( ( ( ( z ( 2nd ` Y ) w ) ` h ) ` y ) ` g ) ) )
154	130, 153	eqtr4d 2659	. . . . . . . . . . 11 |- ( ( ( ( ph /\ ( z e. B /\ w e. B ) ) /\ h e. ( z ( Hom ` C ) w ) ) /\ y e. B ) -> ( g e. ( y ( Hom ` C ) z ) |-> ( ( ( z ( 2nd ` ( ( 1st ` Y ) ` w ) ) y ) ` g ) ` h ) ) = ( ( ( z ( 2nd ` Y ) w ) ` h ) ` y ) )
155	154	mpteq2dva 4744	. . . . . . . . . 10 |- ( ( ( ph /\ ( z e. B /\ w e. B ) ) /\ h e. ( z ( Hom ` C ) w ) ) -> ( y e. B |-> ( g e. ( y ( Hom ` C ) z ) |-> ( ( ( z ( 2nd ` ( ( 1st ` Y ) ` w ) ) y ) ` g ) ` h ) ) ) = ( y e. B |-> ( ( ( z ( 2nd ` Y ) w ) ` h ) ` y ) ) )
156	80	adantr 481	. . . . . . . . . . 11 |- ( ( ( ph /\ ( z e. B /\ w e. B ) ) /\ h e. ( z ( Hom ` C ) w ) ) -> V e. W )
157	81	adantr 481	. . . . . . . . . . 11 |- ( ( ( ph /\ ( z e. B /\ w e. B ) ) /\ h e. ( z ( Hom ` C ) w ) ) -> ran ( Hom f ` C ) C_ U )
158	82	adantr 481	. . . . . . . . . . 11 |- ( ( ( ph /\ ( z e. B /\ w e. B ) ) /\ h e. ( z ( Hom ` C ) w ) ) -> ( ran ( Hom f ` Q ) u. U ) C_ V )
159	22	adantr 481	. . . . . . . . . . 11 |- ( ( ( ph /\ ( z e. B /\ w e. B ) ) /\ h e. ( z ( Hom ` C ) w ) ) -> ( ( 1st ` Y ) ` w ) e. ( O Func S ) )
160	78	eleq2d 2687	. . . . . . . . . . . 12 |- ( ( ph /\ ( z e. B /\ w e. B ) ) -> ( h e. ( ( 1st ` ( ( 1st ` Y ) ` w ) ) ` z ) <-> h e. ( z ( Hom ` C ) w ) ) )
161	160	biimpar 502	. . . . . . . . . . 11 |- ( ( ( ph /\ ( z e. B /\ w e. B ) ) /\ h e. ( z ( Hom ` C ) w ) ) -> h e. ( ( 1st ` ( ( 1st ` Y ) ` w ) ) ` z ) )
162	2, 17, 29, 4, 5, 30, 6, 31, 26, 32, 33, 113, 156, 157, 158, 159, 115, 44, 161	yonedalem4a 16915	. . . . . . . . . 10 |- ( ( ( ph /\ ( z e. B /\ w e. B ) ) /\ h e. ( z ( Hom ` C ) w ) ) -> ( ( ( ( 1st ` Y ) ` w ) N z ) ` h ) = ( y e. B |-> ( g e. ( y ( Hom ` C ) z ) |-> ( ( ( z ( 2nd ` ( ( 1st ` Y ) ` w ) ) y ) ` g ) ` h ) ) ) )
163	99, 134, 48	natfn 16614	. . . . . . . . . . 11 |- ( ( ( ph /\ ( z e. B /\ w e. B ) ) /\ h e. ( z ( Hom ` C ) w ) ) -> ( ( z ( 2nd ` Y ) w ) ` h ) Fn B )
164		dffn5 6241	. . . . . . . . . . 11 |- ( ( ( z ( 2nd ` Y ) w ) ` h ) Fn B <-> ( ( z ( 2nd ` Y ) w ) ` h ) = ( y e. B |-> ( ( ( z ( 2nd ` Y ) w ) ` h ) ` y ) ) )
165	163, 164	sylib 208	. . . . . . . . . 10 |- ( ( ( ph /\ ( z e. B /\ w e. B ) ) /\ h e. ( z ( Hom ` C ) w ) ) -> ( ( z ( 2nd ` Y ) w ) ` h ) = ( y e. B |-> ( ( ( z ( 2nd ` Y ) w ) ` h ) ` y ) ) )
166	155, 162, 165	3eqtr4d 2666	. . . . . . . . 9 |- ( ( ( ph /\ ( z e. B /\ w e. B ) ) /\ h e. ( z ( Hom ` C ) w ) ) -> ( ( ( ( 1st ` Y ) ` w ) N z ) ` h ) = ( ( z ( 2nd ` Y ) w ) ` h ) )
167	166	mpteq2dva 4744	. . . . . . . 8 |- ( ( ph /\ ( z e. B /\ w e. B ) ) -> ( h e. ( z ( Hom ` C ) w ) |-> ( ( ( ( 1st ` Y ) ` w ) N z ) ` h ) ) = ( h e. ( z ( Hom ` C ) w ) |-> ( ( z ( 2nd ` Y ) w ) ` h ) ) )
168		f1of 6137	. . . . . . . . . 10 |- ( ( ( ( 1st ` Y ) ` w ) N z ) : ( z ( Hom ` C ) w ) -1-1-onto-> ( ( ( 1st ` Y ) ` z ) ( O Nat S ) ( ( 1st ` Y ) ` w ) ) -> ( ( ( 1st ` Y ) ` w ) N z ) : ( z ( Hom ` C ) w ) --> ( ( ( 1st ` Y ) ` z ) ( O Nat S ) ( ( 1st ` Y ) ` w ) ) )
169	112, 168	syl 17	. . . . . . . . 9 |- ( ( ph /\ ( z e. B /\ w e. B ) ) -> ( ( ( 1st ` Y ) ` w ) N z ) : ( z ( Hom ` C ) w ) --> ( ( ( 1st ` Y ) ` z ) ( O Nat S ) ( ( 1st ` Y ) ` w ) ) )
170	169	feqmptd 6249	. . . . . . . 8 |- ( ( ph /\ ( z e. B /\ w e. B ) ) -> ( ( ( 1st ` Y ) ` w ) N z ) = ( h e. ( z ( Hom ` C ) w ) |-> ( ( ( ( 1st ` Y ) ` w ) N z ) ` h ) ) )
171	132	feqmptd 6249	. . . . . . . 8 |- ( ( ph /\ ( z e. B /\ w e. B ) ) -> ( z ( 2nd ` Y ) w ) = ( h e. ( z ( Hom ` C ) w ) |-> ( ( z ( 2nd ` Y ) w ) ` h ) ) )
172	167, 170, 171	3eqtr4d 2666	. . . . . . 7 |- ( ( ph /\ ( z e. B /\ w e. B ) ) -> ( ( ( 1st ` Y ) ` w ) N z ) = ( z ( 2nd ` Y ) w ) )
173		f1oeq1 6127	. . . . . . 7 |- ( ( ( ( 1st ` Y ) ` w ) N z ) = ( z ( 2nd ` Y ) w ) -> ( ( ( ( 1st ` Y ) ` w ) N z ) : ( z ( Hom ` C ) w ) -1-1-onto-> ( ( ( 1st ` Y ) ` z ) ( O Nat S ) ( ( 1st ` Y ) ` w ) ) <-> ( z ( 2nd ` Y ) w ) : ( z ( Hom ` C ) w ) -1-1-onto-> ( ( ( 1st ` Y ) ` z ) ( O Nat S ) ( ( 1st ` Y ) ` w ) ) ) )
174	172, 173	syl 17	. . . . . 6 |- ( ( ph /\ ( z e. B /\ w e. B ) ) -> ( ( ( ( 1st ` Y ) ` w ) N z ) : ( z ( Hom ` C ) w ) -1-1-onto-> ( ( ( 1st ` Y ) ` z ) ( O Nat S ) ( ( 1st ` Y ) ` w ) ) <-> ( z ( 2nd ` Y ) w ) : ( z ( Hom ` C ) w ) -1-1-onto-> ( ( ( 1st ` Y ) ` z ) ( O Nat S ) ( ( 1st ` Y ) ` w ) ) ) )
175	112, 174	mpbid 222	. . . . 5 |- ( ( ph /\ ( z e. B /\ w e. B ) ) -> ( z ( 2nd ` Y ) w ) : ( z ( Hom ` C ) w ) -1-1-onto-> ( ( ( 1st ` Y ) ` z ) ( O Nat S ) ( ( 1st ` Y ) ` w ) ) )
176	175	ralrimivva 2971	. . . 4 |- ( ph -> A. z e. B A. w e. B ( z ( 2nd ` Y ) w ) : ( z ( Hom ` C ) w ) -1-1-onto-> ( ( ( 1st ` Y ) ` z ) ( O Nat S ) ( ( 1st ` Y ) ` w ) ) )
177	17, 77, 100	isffth2 16576	. . . 4 |- ( ( 1st ` Y ) ( ( C Full Q ) i^i ( C Faith Q ) ) ( 2nd ` Y ) <-> ( ( 1st ` Y ) ( C Func Q ) ( 2nd ` Y ) /\ A. z e. B A. w e. B ( z ( 2nd ` Y ) w ) : ( z ( Hom ` C ) w ) -1-1-onto-> ( ( ( 1st ` Y ) ` z ) ( O Nat S ) ( ( 1st ` Y ) ` w ) ) ) )
178	16, 176, 177	sylanbrc 698	. . 3 |- ( ph -> ( 1st ` Y ) ( ( C Full Q ) i^i ( C Faith Q ) ) ( 2nd ` Y ) )
179		df-br 4654	. . 3 |- ( ( 1st ` Y ) ( ( C Full Q ) i^i ( C Faith Q ) ) ( 2nd ` Y ) <-> <. ( 1st ` Y ) , ( 2nd ` Y ) >. e. ( ( C Full Q ) i^i ( C Faith Q ) ) )
180	178, 179	sylib 208	. 2 |- ( ph -> <. ( 1st ` Y ) , ( 2nd ` Y ) >. e. ( ( C Full Q ) i^i ( C Faith Q ) ) )
181	14, 180	eqeltrd 2701	1 |- ( ph -> Y e. ( ( C Full Q ) i^i ( C Faith Q ) ) )

Syntax hints:   -> wi 4   <-> wb 196   /\ wa 384   = wceq 1483   e. wcel 1990   A.wral 2912   _Vcvv 3200   u. cun 3572   i^i cin 3573   C_ wss 3574   <.cop 4183   class class class wbr 4653   |-> cmpt 4729   X. cxp 5112   ran crn 5115   Rel wrel 5119   Fn wfn 5883   -->wf 5884   -1-1-onto->wf1o 5887   ` cfv 5888  (class class class)co 6650   |-> cmpt2 6652   1stc1st 7166   2ndc2nd 7167  tpos ctpos 7351   Basecbs 15857   Hom chom 15952  compcco 15953   Catccat 16325   Idccid 16326   Hom _f chomf 16327  oppCatcoppc 16371  Invcinv 16405   Iso ciso 16406   Func cfunc 16514   o._func ccofu 16516   Full cful 16562   Faith cfth 16563   Nat cnat 16601   FuncCat cfuc 16602   SetCatcsetc 16725   X._c cxpc 16808   1st_F c1stf 16809   2nd_F c2ndf 16810   ⟨,⟩_F cprf 16811   eval_F cevlf 16849  Hom_Fchof 16888  Yoncyon 16889

This theorem was proved from axioms:  ax-mp 5  ax-1 6  ax-2 7  ax-3 8  ax-gen 1722  ax-4 1737  ax-5 1839  ax-6 1888  ax-7 1935  ax-8 1992  ax-9 1999  ax-10 2019  ax-11 2034  ax-12 2047  ax-13 2246  ax-ext 2602  ax-rep 4771  ax-sep 4781  ax-nul 4789  ax-pow 4843  ax-pr 4906  ax-un 6949  ax-cnex 9992  ax-resscn 9993  ax-1cn 9994  ax-icn 9995  ax-addcl 9996  ax-addrcl 9997  ax-mulcl 9998  ax-mulrcl 9999  ax-mulcom 10000  ax-addass 10001  ax-mulass 10002  ax-distr 10003  ax-i2m1 10004  ax-1ne0 10005  ax-1rid 10006  ax-rnegex 10007  ax-rrecex 10008  ax-cnre 10009  ax-pre-lttri 10010  ax-pre-lttrn 10011  ax-pre-ltadd 10012  ax-pre-mulgt0 10013

This theorem depends on definitions:  df-bi 197  df-or 385  df-an 386  df-3or 1038  df-3an 1039  df-tru 1486  df-fal 1489  df-ex 1705  df-nf 1710  df-sb 1881  df-eu 2474  df-mo 2475  df-clab 2609  df-cleq 2615  df-clel 2618  df-nfc 2753  df-ne 2795  df-nel 2898  df-ral 2917  df-rex 2918  df-reu 2919  df-rmo 2920  df-rab 2921  df-v 3202  df-sbc 3436  df-csb 3534  df-dif 3577  df-un 3579  df-in 3581  df-ss 3588  df-pss 3590  df-nul 3916  df-if 4087  df-pw 4160  df-sn 4178  df-pr 4180  df-tp 4182  df-op 4184  df-uni 4437  df-int 4476  df-iun 4522  df-br 4654  df-opab 4713  df-mpt 4730  df-tr 4753  df-id 5024  df-eprel 5029  df-po 5035  df-so 5036  df-fr 5073  df-we 5075  df-xp 5120  df-rel 5121  df-cnv 5122  df-co 5123  df-dm 5124  df-rn 5125  df-res 5126  df-ima 5127  df-pred 5680  df-ord 5726  df-on 5727  df-lim 5728  df-suc 5729  df-iota 5851  df-fun 5890  df-fn 5891  df-f 5892  df-f1 5893  df-fo 5894  df-f1o 5895  df-fv 5896  df-riota 6611  df-ov 6653  df-oprab 6654  df-mpt2 6655  df-om 7066  df-1st 7168  df-2nd 7169  df-tpos 7352  df-wrecs 7407  df-recs 7468  df-rdg 7506  df-1o 7560  df-oadd 7564  df-er 7742  df-map 7859  df-pm 7860  df-ixp 7909  df-en 7956  df-dom 7957  df-sdom 7958  df-fin 7959  df-pnf 10076  df-mnf 10077  df-xr 10078  df-ltxr 10079  df-le 10080  df-sub 10268  df-neg 10269  df-nn 11021  df-2 11079  df-3 11080  df-4 11081  df-5 11082  df-6 11083  df-7 11084  df-8 11085  df-9 11086  df-n0 11293  df-z 11378  df-dec 11494  df-uz 11688  df-fz 12327  df-struct 15859  df-ndx 15860  df-slot 15861  df-base 15863  df-sets 15864  df-ress 15865  df-hom 15966  df-cco 15967  df-cat 16329  df-cid 16330  df-homf 16331  df-comf 16332  df-oppc 16372  df-sect 16407  df-inv 16408  df-iso 16409  df-ssc 16470  df-resc 16471  df-subc 16472  df-func 16518  df-cofu 16520  df-full 16564  df-fth 16565  df-nat 16603  df-fuc 16604  df-setc 16726  df-xpc 16812  df-1stf 16813  df-2ndf 16814  df-prf 16815  df-evlf 16853  df-curf 16854  df-hof 16890  df-yon 16891

This theorem is referenced by:  yonffth  16924