Nearby theorems
|
|
Metamath Proof Explorer |
< Previous
Next >
Nearby theorems |
|
| Mirrors > Home > MPE Home > Th. List > dipcj | Structured version Visualization version Unicode version | ||
| Description: The complex conjugate of an inner product reverses its arguments. Equation I1 of [Ponnusamy] p. 362. (Contributed by NM, 1-Feb-2007.) (New usage is discouraged.) |
| Ref | Expression |
|---|---|
| ipcl.1 |
        |
| ipcl.7 |
   |
| Ref | Expression |
|---|---|
| dipcj |
  ![/\](wedge.gif "/\"){kind=small} 
   |
| Step | Hyp | Ref | Expression |
|---|---|---|---|
| 1 | ipcl.1 |
. . . 4
| |
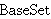| 2 | eqid 2622 |
. . . 4
 | |
| 3 | eqid 2622 |
. . . 4
 | |
| 4 | eqid 2622 |
. . . 4
 CV CV | |
| 5 | ipcl.7 |
. . . 4
| |
| 6 | 1, 2, 3, 4, 5 | ipval2 27562 |
. . 3
CV   CV     CV CV   |
| 7 | 6 | fveq2d 6195 |
. 2
CV CV CV CV |
| 8 | 1, 2, 3, 4, 5 | ipval2 27562 |
. . . 4
CV CV CV CV |
| 9 | 8 | 3com23 1271 |
. . 3
CV CV CV CV |
| 10 | 1, 2, 3, 4, 5 | ipval2lem3 27560 |
. . . . . . . 8
CV  |
| 11 | 10 | recnd 10068 |
. . . . . . 7
CV  |
| 12 | neg1cn 11124 |
. . . . . . . 8
| |
| 13 | 1, 2, 3, 4, 5 | ipval2lem4 27561 |
. . . . . . . 8
CV |
| 14 | 12, 13 | mpan2 707 |
. . . . . . 7
CV |
| 15 | 11, 14 | subcld 10392 |
. . . . . 6
CV CV |
| 16 | ax-icn 9995 |
. . . . . . 7
| |
| 17 | 1, 2, 3, 4, 5 | ipval2lem4 27561 |
. . . . . . . . 9
CV |
| 18 | 16, 17 | mpan2 707 |
. . . . . . . 8
CV |
| 19 | negicn 10282 |
. . . . . . . . 9
| |
| 20 | 1, 2, 3, 4, 5 | ipval2lem4 27561 |
. . . . . . . . 9
CV |
| 21 | 19, 20 | mpan2 707 |
. . . . . . . 8
CV |
| 22 | 18, 21 | subcld 10392 |
. . . . . . 7
CV CV |
| 23 | mulcl 10020 |
. . . . . . 7
CV CV CV CV | |
| 24 | 16, 22, 23 | sylancr 695 |
. . . . . 6
CV CV |
| 25 | 15, 24 | addcld 10059 |
. . . . 5
CV CV CV CV |
| 26 | 4cn 11098 |
. . . . . 6
| |
| 27 | 4ne0 11117 |
. . . . . 6
  | |
| 28 | cjdiv 13904 |
. . . . . 6
CV CV CV CV CV CV CV CV CV CV CV CV | |
| 29 | 26, 27, 28 | mp3an23 1416 |
. . . . 5
CV CV CV CV CV CV CV CV CV CV CV CV |
| 30 | 25, 29 | syl 17 |
. . . 4
CV CV CV CV CV CV CV CV |
| 31 | 4re 11097 |
. . . . . . 7
| |
| 32 | cjre 13879 |
. . . . . . 7
| |
| 33 | 31, 32 | ax-mp 5 |
. . . . . 6
|
| 34 | 33 | oveq2i 6661 |
. . . . 5
CV CV CV CV CV CV CV CV |
| 35 | 1, 2, 3, 4, 5 | ipval2lem2 27559 |
. . . . . . . . . 10
CV |
| 36 | 12, 35 | mpan2 707 |
. . . . . . . . 9
CV |
| 37 | 10, 36 | resubcld 10458 |
. . . . . . . 8
CV CV |
| 38 | 1, 2, 3, 4, 5 | ipval2lem2 27559 |
. . . . . . . . . 10
CV |
| 39 | 16, 38 | mpan2 707 |
. . . . . . . . 9
CV |
| 40 | 1, 2, 3, 4, 5 | ipval2lem2 27559 |
. . . . . . . . . 10
CV |
| 41 | 19, 40 | mpan2 707 |
. . . . . . . . 9
CV |
| 42 | 39, 41 | resubcld 10458 |
. . . . . . . 8
CV CV |
| 43 | cjreim 13900 |
. . . . . . . 8
CV CV CV CV CV CV CV CV CV CV
CV CV | |
| 44 | 37, 42, 43 | syl2anc 693 |
. . . . . . 7
CV CV CV CV CV CV
CV CV |
| 45 | submul2 10470 |
. . . . . . . . 9
CV CV CV CV CV CV
CV CV CV CV CV CV | |
| 46 | 16, 45 | mp3an2 1412 |
. . . . . . . 8
CV CV CV CV CV CV
CV CV CV CV CV CV |
| 47 | 15, 22, 46 | syl2anc 693 |
. . . . . . 7
CV CV
CV CV CV CV CV CV |
| 48 | 1, 2 | nvcom 27476 |
. . . . . . . . . . 11
|
| 49 | 48 | fveq2d 6195 |
. . . . . . . . . 10
CV CV |
| 50 | 49 | oveq1d 6665 |
. . . . . . . . 9
CV CV |
| 51 | 1, 2, 3, 4 | nvdif 27521 |
. . . . . . . . . 10
CV CV |
| 52 | 51 | oveq1d 6665 |
. . . . . . . . 9
CV CV |
| 53 | 50, 52 | oveq12d 6668 |
. . . . . . . 8
CV CV CV CV |
| 54 | 18, 21 | negsubdi2d 10408 |
. . . . . . . . . 10
CV CV CV CV |
| 55 | 1, 2, 3, 4 | nvpi 27522 |
. . . . . . . . . . . . . 14
CV CV |
| 56 | 55 | 3com23 1271 |
. . . . . . . . . . . . 13
CV CV |
| 57 | 56 | eqcomd 2628 |
. . . . . . . . . . . 12
CV CV |
| 58 | 57 | oveq1d 6665 |
. . . . . . . . . . 11
CV CV |
| 59 | 1, 2, 3, 4 | nvpi 27522 |
. . . . . . . . . . . 12
CV CV |
| 60 | 59 | oveq1d 6665 |
. . . . . . . . . . 11
CV CV |
| 61 | 58, 60 | oveq12d 6668 |
. . . . . . . . . 10
CV CV CV CV |
| 62 | 54, 61 | eqtrd 2656 |
. . . . . . . . 9
CV CV CV CV |
| 63 | 62 | oveq2d 6666 |
. . . . . . . 8
CV CV CV CV |
| 64 | 53, 63 | oveq12d 6668 |
. . . . . . 7
CV CV CV CV CV CV CV CV |
| 65 | 44, 47, 64 | 3eqtrd 2660 |
. . . . . 6
CV CV CV CV CV CV CV CV |
| 66 | 65 | oveq1d 6665 |
. . . . 5
CV CV CV CV CV CV CV CV |
| 67 | 34, 66 | syl5eq 2668 |
. . . 4
CV CV CV CV CV CV CV CV |
| 68 | 30, 67 | eqtrd 2656 |
. . 3
CV CV CV CV CV CV CV CV |
| 69 | 9, 68 | eqtr4d 2659 |
. 2
CV CV CV CV |
| 70 | 7, 69 | eqtr4d 2659 |
1
|
| Colors of variables: wff setvar class |
| Syntax hints: wi 4
w3a 1037
wceq 1483
wcel 1990
wne 2794
cfv 5888
(class class class)co 6650 cc 9934 cr 9935 cc0 9936 c1 9937 ci 9938 caddc 9939 cmul 9941 cmin 10266 cneg 10267 cdiv 10684 c2 11070 c4 11072 cexp 12860 ccj 13836 cnv 27439 cpv 27440 cba 27441 cns 27442 CVcnmcv 27445 cdip 27555 |
| This theorem was proved from axioms: ax-mp 5 ax-1 6 ax-2 7 ax-3 8 ax-gen 1722 ax-4 1737 ax-5 1839 ax-6 1888 ax-7 1935 ax-8 1992 ax-9 1999 ax-10 2019 ax-11 2034 ax-12 2047 ax-13 2246 ax-ext 2602 ax-rep 4771 ax-sep 4781 ax-nul 4789 ax-pow 4843 ax-pr 4906 ax-un 6949 ax-inf2 8538 ax-cnex 9992 ax-resscn 9993 ax-1cn 9994 ax-icn 9995 ax-addcl 9996 ax-addrcl 9997 ax-mulcl 9998 ax-mulrcl 9999 ax-mulcom 10000 ax-addass 10001 ax-mulass 10002 ax-distr 10003 ax-i2m1 10004 ax-1ne0 10005 ax-1rid 10006 ax-rnegex 10007 ax-rrecex 10008 ax-cnre 10009 ax-pre-lttri 10010 ax-pre-lttrn 10011 ax-pre-ltadd 10012 ax-pre-mulgt0 10013 ax-pre-sup 10014 |
| This theorem depends on definitions: df-bi 197 df-or 385 df-an 386 df-3or 1038 df-3an 1039 df-tru 1486 df-fal 1489 df-ex 1705 df-nf 1710 df-sb 1881 df-eu 2474 df-mo 2475 df-clab 2609 df-cleq 2615 df-clel 2618 df-nfc 2753 df-ne 2795 df-nel 2898 df-ral 2917 df-rex 2918 df-reu 2919 df-rmo 2920 df-rab 2921 df-v 3202 df-sbc 3436 df-csb 3534 df-dif 3577 df-un 3579 df-in 3581 df-ss 3588 df-pss 3590 df-nul 3916 df-if 4087 df-pw 4160 df-sn 4178 df-pr 4180 df-tp 4182 df-op 4184 df-uni 4437 df-int 4476 df-iun 4522 df-br 4654 df-opab 4713 df-mpt 4730 df-tr 4753 df-id 5024 df-eprel 5029 df-po 5035 df-so 5036 df-fr 5073 df-se 5074 df-we 5075 df-xp 5120 df-rel 5121 df-cnv 5122 df-co 5123 df-dm 5124 df-rn 5125 df-res 5126 df-ima 5127 df-pred 5680 df-ord 5726 df-on 5727 df-lim 5728 df-suc 5729 df-iota 5851 df-fun 5890 df-fn 5891 df-f 5892 df-f1 5893 df-fo 5894 df-f1o 5895 df-fv 5896 df-isom 5897 df-riota 6611 df-ov 6653 df-oprab 6654 df-mpt2 6655 df-om 7066 df-1st 7168 df-2nd 7169 df-wrecs 7407 df-recs 7468 df-rdg 7506 df-1o 7560 df-oadd 7564 df-er 7742 df-en 7956 df-dom 7957 df-sdom 7958 df-fin 7959 df-sup 8348 df-oi 8415 df-card 8765 df-pnf 10076 df-mnf 10077 df-xr 10078 df-ltxr 10079 df-le 10080 df-sub 10268 df-neg 10269 df-div 10685 df-nn 11021 df-2 11079 df-3 11080 df-4 11081 df-n0 11293 df-z 11378 df-uz 11688 df-rp 11833 df-fz 12327 df-fzo 12466 df-seq 12802 df-exp 12861 df-hash 13118 df-cj 13839 df-re 13840 df-im 13841 df-sqrt 13975 df-abs 13976 df-clim 14219 df-sum 14417 df-grpo 27347 df-gid 27348 df-ginv 27349 df-ablo 27399 df-vc 27414 df-nv 27447 df-va 27450 df-ba 27451 df-sm 27452 df-0v 27453 df-nmcv 27455 df-dip 27556 |
| This theorem is referenced by: ipipcj 27570 diporthcom 27571 dip0l 27573 ipasslem10 27694 dipdi 27698 dipassr 27701 dipsubdi 27704 siii 27708 hlipcj 27767 |
| Copyright terms: Public domain | W3C validator |