Users' Mathboxes Mathbox for Richard Penner < Previous   Next >
Nearby theorems
Mirrors  >  Home  >  MPE Home  >  Th. List  >   Mathboxes  >  cotrclrcl Structured version   Visualization version   Unicode version
Theorem cotrclrcl 38034
Description: The composition of the reflexive and transitive closures is the reflexive-transitive closure. (Contributed by RP, 21-Jun-2020.)
Assertion
Ref Expression
cotrclrcl |- ( t+ o. r* ) = t*
Proof of Theorem cotrclrcl
Dummy variables a b c d i j k x y are mutually distinct and distinct from all other variables.
StepHypRef Expression
1 dftrcl3 38012 . 2 |- t+ = ( a e. _V |-> U_ i e. NN ( a ^r i ) )
2 dfrcl4 37968 . 2 |- r* = ( b e. _V |-> U_ j e. { 0 , 1 } ( b ^r j ) )
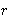
3 dfrtrcl3 38025 . 2 |- t* = ( c e. _V |-> U_ k e. NN0 ( c ^r k ) )
4 nnex 11026 . 2 |- NN e. _V
5 prex 4909 . 2 |- { 0 , 1 } e. _V
6 df-n0 11293 . . 3 |- NN0 = ( NN u. { 0 } )
7 df-pr 4180 . . . . . 6 |- { 0 , 1 } = ( { 0 } u. { 1 } )
87equncomi 3759 . . . . 5 |- { 0 , 1 } = ( { 1 } u. { 0 } )
98uneq2i 3764 . . . 4 |- ( NN u. { 0 , 1 } ) = ( NN u. ( { 1 } u. { 0 } ) )
10 unass 3770 . . . 4 |- ( ( NN u. { 1 } ) u. { 0 } ) = ( NN u. ( { 1 } u. { 0 } ) )
11 1nn 11031 . . . . . . 7 |- 1 e. NN
12 snssi 4339 . . . . . . 7 |- ( 1 e. NN -> { 1 } C_ NN )
1311, 12ax-mp 5 . . . . . 6 |- { 1 } C_ NN
14 ssequn2 3786 . . . . . 6 |- ( { 1 } C_ NN <-> ( NN u. { 1 } ) = NN )
1513, 14mpbi 220 . . . . 5 |- ( NN u. { 1 } ) = NN
1615uneq1i 3763 . . . 4 |- ( ( NN u. { 1 } ) u. { 0 } ) = ( NN u. { 0 } )
179, 10, 163eqtr2ri 2651 . . 3 |- ( NN u. { 0 } ) = ( NN u. { 0 , 1 } )
186, 17eqtri 2644 . 2 |- NN0 = ( NN u. { 0 , 1 } )
19 oveq2 6658 . . . 4 |- ( k = i -> ( d ^r k ) = ( d ^r i ) )
2019cbviunv 4559 . . 3 |- U_ k e. NN ( d ^r k ) = U_ i e. NN ( d ^r i )
21 ss2iun 4536 . . . 4 |- ( A. i e. NN ( d ^r i ) C_ ( U_ j e. { 0 , 1 } ( d ^r j ) ^r i ) -> U_ i e. NN ( d ^r i ) C_ U_ i e. NN ( U_ j e. { 0 , 1 } ( d ^r j ) ^r i ) )
22 1ex 10035 . . . . . . . 8 |- 1 e. _V
2322prid2 4298 . . . . . . 7 |- 1 e. { 0 , 1 }
24 oveq2 6658 . . . . . . . . 9 |- ( j = 1 -> ( d ^r j ) = ( d ^r 1 ) )
25 vex 3203 . . . . . . . . . 10 |- d e. _V
26 relexp1g 13766 . . . . . . . . . 10 |- ( d e. _V -> ( d ^r 1 ) = d )
2725, 26ax-mp 5 . . . . . . . . 9 |- ( d ^r 1 ) = d
2824, 27syl6eq 2672 . . . . . . . 8 |- ( j = 1 -> ( d ^r j ) = d )
2928ssiun2s 4564 . . . . . . 7 |- ( 1 e. { 0 , 1 } -> d C_ U_ j e. { 0 , 1 } ( d ^r j ) )
3023, 29ax-mp 5 . . . . . 6 |- d C_ U_ j e. { 0 , 1 } ( d ^r j )
3130a1i 11 . . . . 5 |- ( i e. NN -> d C_ U_ j e. { 0 , 1 } ( d ^r j ) )
32 ovex 6678 . . . . . . 7 |- ( d ^r j ) e. _V
335, 32iunex 7147 . . . . . 6 |- U_ j e. { 0 , 1 } ( d ^r j ) e. _V
3433a1i 11 . . . . 5 |- ( i e. NN -> U_ j e. { 0 , 1 } ( d ^r j ) e. _V )
35 nnnn0 11299 . . . . 5 |- ( i e. NN -> i e. NN0 )
3631, 34, 35relexpss1d 37997 . . . 4 |- ( i e. NN -> ( d ^r i ) C_ ( U_ j e. { 0 , 1 } ( d ^r j ) ^r i ) )
3721, 36mprg 2926 . . 3 |- U_ i e. NN ( d ^r i ) C_ U_ i e. NN ( U_ j e. { 0 , 1 } ( d ^r j ) ^r i )
3820, 37eqsstri 3635 . 2 |- U_ k e. NN ( d ^r k ) C_ U_ i e. NN ( U_ j e. { 0 , 1 } ( d ^r j ) ^r i )
39 oveq2 6658 . . . . 5 |- ( i = 1 -> ( U_ j e. { 0 , 1 } ( d ^r j ) ^r i ) = ( U_ j e. { 0 , 1 } ( d ^r j ) ^r 1 ) )
40 relexp1g 13766 . . . . . . 7 |- ( U_ j e. { 0 , 1 } ( d ^r j ) e. _V -> ( U_ j e. { 0 , 1 } ( d ^r j ) ^r 1 ) = U_ j e. { 0 , 1 } ( d ^r j ) )
4133, 40ax-mp 5 . . . . . 6 |- ( U_ j e. { 0 , 1 } ( d ^r j ) ^r 1 ) = U_ j e. { 0 , 1 } ( d ^r j )
42 oveq2 6658 . . . . . . 7 |- ( j = k -> ( d ^r j ) = ( d ^r k ) )
4342cbviunv 4559 . . . . . 6 |- U_ j e. { 0 , 1 } ( d ^r j ) = U_ k e. { 0 , 1 } ( d ^r k )
4441, 43eqtri 2644 . . . . 5 |- ( U_ j e. { 0 , 1 } ( d ^r j ) ^r 1 ) = U_ k e. { 0 , 1 } ( d ^r k )
4539, 44syl6eq 2672 . . . 4 |- ( i = 1 -> ( U_ j e. { 0 , 1 } ( d ^r j ) ^r i ) = U_ k e. { 0 , 1 } ( d ^r k ) )
4645ssiun2s 4564 . . 3 |- ( 1 e. NN -> U_ k e. { 0 , 1 } ( d ^r k ) C_ U_ i e. NN ( U_ j e. { 0 , 1 } ( d ^r j ) ^r i ) )
4711, 46ax-mp 5 . 2 |- U_ k e. { 0 , 1 } ( d ^r k ) C_ U_ i e. NN ( U_ j e. { 0 , 1 } ( d ^r j ) ^r i )
48 iunss 4561 . . . 4 |- ( U_ i e. NN ( U_ j e. { 0 , 1 } ( d ^r j ) ^r i ) C_ U_ k e. NN0 ( d ^r k ) <-> A. i e. NN ( U_ j e. { 0 , 1 } ( d ^r j ) ^r i ) C_ U_ k e. NN0 ( d ^r k ) )
49 iuneq1 4534 . . . . . . . 8 |- ( { 0 , 1 } = ( { 0 } u. { 1 } ) -> U_ j e. { 0 , 1 } ( d ^r j ) = U_ j e. ( { 0 } u. { 1 } ) ( d ^r j ) )
507, 49ax-mp 5 . . . . . . 7 |- U_ j e. { 0 , 1 } ( d ^r j ) = U_ j e. ( { 0 } u. { 1 } ) ( d ^r j )
51 iunxun 4605 . . . . . . 7 |- U_ j e. ( { 0 } u. { 1 } ) ( d ^r j ) = ( U_ j e. { 0 } ( d ^r j ) u. U_ j e. { 1 } ( d ^r j ) )
52 c0ex 10034 . . . . . . . . 9 |- 0 e. _V
53 oveq2 6658 . . . . . . . . 9 |- ( j = 0 -> ( d ^r j ) = ( d ^r 0 ) )
5452, 53iunxsn 4603 . . . . . . . 8 |- U_ j e. { 0 } ( d ^r j ) = ( d ^r 0 )
5522, 24iunxsn 4603 . . . . . . . 8 |- U_ j e. { 1 } ( d ^r j ) = ( d ^r 1 )
5654, 55uneq12i 3765 . . . . . . 7 |- ( U_ j e. { 0 } ( d ^r j ) u. U_ j e. { 1 } ( d ^r j ) ) = ( ( d ^r 0 ) u. ( d ^r 1 ) )
5750, 51, 563eqtri 2648 . . . . . 6 |- U_ j e. { 0 , 1 } ( d ^r j ) = ( ( d ^r 0 ) u. ( d ^r 1 ) )
5857oveq1i 6660 . . . . 5 |- ( U_ j e. { 0 , 1 } ( d ^r j ) ^r i ) = ( ( ( d ^r 0 ) u. ( d ^r 1 ) ) ^r i )
59 oveq2 6658 . . . . . . 7 |- ( x = 1 -> ( ( ( d ^r 0 ) u. ( d ^r 1 ) ) ^r x ) = ( ( ( d ^r 0 ) u. ( d ^r 1 ) ) ^r 1 ) )
6059sseq1d 3632 . . . . . 6 |- ( x = 1 -> ( ( ( ( d ^r 0 ) u. ( d ^r 1 ) ) ^r x ) C_ U_ k e. NN0 ( d ^r k ) <-> ( ( ( d ^r 0 ) u. ( d ^r 1 ) ) ^r 1 ) C_ U_ k e. NN0 ( d ^r k ) ) )
61 oveq2 6658 . . . . . . 7 |- ( x = y -> ( ( ( d ^r 0 ) u. ( d ^r 1 ) ) ^r x ) = ( ( ( d ^r 0 ) u. ( d ^r 1 ) ) ^r y ) )
6261sseq1d 3632 . . . . . 6 |- ( x = y -> ( ( ( ( d ^r 0 ) u. ( d ^r 1 ) ) ^r x ) C_ U_ k e. NN0 ( d ^r k ) <-> ( ( ( d ^r 0 ) u. ( d ^r 1 ) ) ^r y ) C_ U_ k e. NN0 ( d ^r k ) ) )
63 oveq2 6658 . . . . . . 7 |- ( x = ( y + 1 ) -> ( ( ( d ^r 0 ) u. ( d ^r 1 ) ) ^r x ) = ( ( ( d ^r 0 ) u. ( d ^r 1 ) ) ^r ( y + 1 ) ) )
6463sseq1d 3632 . . . . . 6 |- ( x = ( y + 1 ) -> ( ( ( ( d ^r 0 ) u. ( d ^r 1 ) ) ^r x ) C_ U_ k e. NN0 ( d ^r k ) <-> ( ( ( d ^r 0 ) u. ( d ^r 1 ) ) ^r ( y + 1 ) ) C_ U_ k e. NN0 ( d ^r k ) ) )
65 oveq2 6658 . . . . . . 7 |- ( x = i -> ( ( ( d ^r 0 ) u. ( d ^r 1 ) ) ^r x ) = ( ( ( d ^r 0 ) u. ( d ^r 1 ) ) ^r i ) )
6665sseq1d 3632 . . . . . 6 |- ( x = i -> ( ( ( ( d ^r 0 ) u. ( d ^r 1 ) ) ^r x ) C_ U_ k e. NN0 ( d ^r k ) <-> ( ( ( d ^r 0 ) u. ( d ^r 1 ) ) ^r i ) C_ U_ k e. NN0 ( d ^r k ) ) )
67 ovex 6678 . . . . . . . . 9 |- ( d ^r 0 ) e. _V
68 ovex 6678 . . . . . . . . 9 |- ( d ^r 1 ) e. _V
6967, 68unex 6956 . . . . . . . 8 |- ( ( d ^r 0 ) u. ( d ^r 1 ) ) e. _V
70 relexp1g 13766 . . . . . . . 8 |- ( ( ( d ^r 0 ) u. ( d ^r 1 ) ) e. _V -> ( ( ( d ^r 0 ) u. ( d ^r 1 ) ) ^r 1 ) = ( ( d ^r 0 ) u. ( d ^r 1 ) ) )
7169, 70ax-mp 5 . . . . . . 7 |- ( ( ( d ^r 0 ) u. ( d ^r 1 ) ) ^r 1 ) = ( ( d ^r 0 ) u. ( d ^r 1 ) )
72 0nn0 11307 . . . . . . . . 9 |- 0 e. NN0
73 oveq2 6658 . . . . . . . . . 10 |- ( k = 0 -> ( d ^r k ) = ( d ^r 0 ) )
7473ssiun2s 4564 . . . . . . . . 9 |- ( 0 e. NN0 -> ( d ^r 0 ) C_ U_ k e. NN0 ( d ^r k ) )
7572, 74ax-mp 5 . . . . . . . 8 |- ( d ^r 0 ) C_ U_ k e. NN0 ( d ^r k )
76 1nn0 11308 . . . . . . . . 9 |- 1 e. NN0
77 oveq2 6658 . . . . . . . . . 10 |- ( k = 1 -> ( d ^r k ) = ( d ^r 1 ) )
7877ssiun2s 4564 . . . . . . . . 9 |- ( 1 e. NN0 -> ( d ^r 1 ) C_ U_ k e. NN0 ( d ^r k ) )
7976, 78ax-mp 5 . . . . . . . 8 |- ( d ^r 1 ) C_ U_ k e. NN0 ( d ^r k )
8075, 79unssi 3788 . . . . . . 7 |- ( ( d ^r 0 ) u. ( d ^r 1 ) ) C_ U_ k e. NN0 ( d ^r k )
8171, 80eqsstri 3635 . . . . . 6 |- ( ( ( d ^r 0 ) u. ( d ^r 1 ) ) ^r 1 ) C_ U_ k e. NN0 ( d ^r k )
82 simpl 473 . . . . . . . . 9 |- ( ( y e. NN /\ ( ( ( d ^r 0 ) u. ( d ^r 1 ) ) ^r y ) C_ U_ k e. NN0 ( d ^r k ) ) -> y e. NN )
83 relexpsucnnr 13765 . . . . . . . . 9 |- ( ( ( ( d ^r 0 ) u. ( d ^r 1 ) ) e. _V /\ y e. NN ) -> ( ( ( d ^r 0 ) u. ( d ^r 1 ) ) ^r ( y + 1 ) ) = ( ( ( ( d ^r 0 ) u. ( d ^r 1 ) ) ^r y ) o. ( ( d ^r 0 ) u. ( d ^r 1 ) ) ) )
8469, 82, 83sylancr 695 . . . . . . . 8 |- ( ( y e. NN /\ ( ( ( d ^r 0 ) u. ( d ^r 1 ) ) ^r y ) C_ U_ k e. NN0 ( d ^r k ) ) -> ( ( ( d ^r 0 ) u. ( d ^r 1 ) ) ^r ( y + 1 ) ) = ( ( ( ( d ^r 0 ) u. ( d ^r 1 ) ) ^r y ) o. ( ( d ^r 0 ) u. ( d ^r 1 ) ) ) )
85 coss1 5277 . . . . . . . . . 10 |- ( ( ( ( d ^r 0 ) u. ( d ^r 1 ) ) ^r y ) C_ U_ k e. NN0 ( d ^r k ) -> ( ( ( ( d ^r 0 ) u. ( d ^r 1 ) ) ^r y ) o. ( ( d ^r 0 ) u. ( d ^r 1 ) ) ) C_ ( U_ k e. NN0 ( d ^r k ) o. ( ( d ^r 0 ) u. ( d ^r 1 ) ) ) )
86 coundi 5636 . . . . . . . . . . 11 |- ( U_ k e. NN0 ( d ^r k ) o. ( ( d ^r 0 ) u. ( d ^r 1 ) ) ) = ( ( U_ k e. NN0 ( d ^r k ) o. ( d ^r 0 ) ) u. ( U_ k e. NN0 ( d ^r k ) o. ( d ^r 1 ) ) )
87 relexp0g 13762 . . . . . . . . . . . . . . . 16 |- ( d e. _V -> ( d ^r 0 ) = ( _I |` ( dom d u. ran d ) ) )
8825, 87ax-mp 5 . . . . . . . . . . . . . . 15 |- ( d ^r 0 ) = ( _I |` ( dom d u. ran d ) )
8988coeq2i 5282 . . . . . . . . . . . . . 14 |- ( U_ k e. NN0 ( d ^r k ) o. ( d ^r 0 ) ) = ( U_ k e. NN0 ( d ^r k ) o. ( _I |` ( dom d u. ran d ) ) )
90 coiun1 37944 . . . . . . . . . . . . . 14 |- ( U_ k e. NN0 ( d ^r k ) o. ( _I |` ( dom d u. ran d ) ) ) = U_ k e. NN0 ( ( d ^r k ) o. ( _I |` ( dom d u. ran d ) ) )
91 coires1 5653 . . . . . . . . . . . . . . . 16 |- ( ( d ^r k ) o. ( _I |` ( dom d u. ran d ) ) ) = ( ( d ^r k ) |` ( dom d u. ran d ) )
9291a1i 11 . . . . . . . . . . . . . . 15 |- ( k e. NN0 -> ( ( d ^r k ) o. ( _I |` ( dom d u. ran d ) ) ) = ( ( d ^r k ) |` ( dom d u. ran d ) ) )
9392iuneq2i 4539 . . . . . . . . . . . . . 14 |- U_ k e. NN0 ( ( d ^r k ) o. ( _I |` ( dom d u. ran d ) ) ) = U_ k e. NN0 ( ( d ^r k ) |` ( dom d u. ran d ) )
9489, 90, 933eqtri 2648 . . . . . . . . . . . . 13 |- ( U_ k e. NN0 ( d ^r k ) o. ( d ^r 0 ) ) = U_ k e. NN0 ( ( d ^r k ) |` ( dom d u. ran d ) )
95 ss2iun 4536 . . . . . . . . . . . . . 14 |- ( A. k e. NN0 ( ( d ^r k ) |` ( dom d u. ran d ) ) C_ ( d ^r k ) -> U_ k e. NN0 ( ( d ^r k ) |` ( dom d u. ran d ) ) C_ U_ k e. NN0 ( d ^r k ) )
96 resss 5422 . . . . . . . . . . . . . . 15 |- ( ( d ^r k ) |` ( dom d u. ran d ) ) C_ ( d ^r k )
9796a1i 11 . . . . . . . . . . . . . 14 |- ( k e. NN0 -> ( ( d ^r k ) |` ( dom d u. ran d ) ) C_ ( d ^r k ) )
9895, 97mprg 2926 . . . . . . . . . . . . 13 |- U_ k e. NN0 ( ( d ^r k ) |` ( dom d u. ran d ) ) C_ U_ k e. NN0 ( d ^r k )
9994, 98eqsstri 3635 . . . . . . . . . . . 12 |- ( U_ k e. NN0 ( d ^r k ) o. ( d ^r 0 ) ) C_ U_ k e. NN0 ( d ^r k )
100 coiun1 37944 . . . . . . . . . . . . . 14 |- ( U_ k e. NN0 ( d ^r k ) o. ( d ^r 1 ) ) = U_ k e. NN0 ( ( d ^r k ) o. ( d ^r 1 ) )
101 iunss2 4565 . . . . . . . . . . . . . . 15 |- ( A. k e. NN0 E. i e. NN0 ( ( d ^r k ) o. ( d ^r 1 ) ) C_ ( d ^r i ) -> U_ k e. NN0 ( ( d ^r k ) o. ( d ^r 1 ) ) C_ U_ i e. NN0 ( d ^r i ) )
102 peano2nn0 11333 . . . . . . . . . . . . . . . . . . 19 |- ( k e. NN0 -> ( k + 1 ) e. NN0 )
103 sbcel1v 3495 . . . . . . . . . . . . . . . . . . 19 |- ( [. ( k + 1 ) / i ]. i e. NN0 <-> ( k + 1 ) e. NN0 )
104102, 103sylibr 224 . . . . . . . . . . . . . . . . . 18 |- ( k e. NN0 -> [. ( k + 1 ) / i ]. i e. NN0 )
105 relexpaddss 38010 . . . . . . . . . . . . . . . . . . . . 21 |- ( ( k e. NN0 /\ 1 e. NN0 /\ d e. _V ) -> ( ( d ^r k ) o. ( d ^r 1 ) ) C_ ( d ^r ( k + 1 ) ) )
10676, 25, 105mp3an23 1416 . . . . . . . . . . . . . . . . . . . 20 |- ( k e. NN0 -> ( ( d ^r k ) o. ( d ^r 1 ) ) C_ ( d ^r ( k + 1 ) ) )
107 ovex 6678 . . . . . . . . . . . . . . . . . . . . 21 |- ( k + 1 ) e. _V
108 csbconstg 3546 . . . . . . . . . . . . . . . . . . . . 21 |- ( ( k + 1 ) e. _V -> [_ ( k + 1 ) / i ]_ ( ( d ^r k ) o. ( d ^r 1 ) ) = ( ( d ^r k ) o. ( d ^r 1 ) ) )
109107, 108ax-mp 5 . . . . . . . . . . . . . . . . . . . 20 |- [_ ( k + 1 ) / i ]_ ( ( d ^r k ) o. ( d ^r 1 ) ) = ( ( d ^r k ) o. ( d ^r 1 ) )
110 csbov2g 6691 . . . . . . . . . . . . . . . . . . . . . 22 |- ( ( k + 1 ) e. _V -> [_ ( k + 1 ) / i ]_ ( d ^r i ) = ( d ^r [_ ( k + 1 ) / i ]_ i ) )
111 csbvarg 4003 . . . . . . . . . . . . . . . . . . . . . . 23 |- ( ( k + 1 ) e. _V -> [_ ( k + 1 ) / i ]_ i = ( k + 1 ) )
112111oveq2d 6666 . . . . . . . . . . . . . . . . . . . . . 22 |- ( ( k + 1 ) e. _V -> ( d ^r [_ ( k + 1 ) / i ]_ i ) = ( d ^r ( k + 1 ) ) )
113110, 112eqtrd 2656 . . . . . . . . . . . . . . . . . . . . 21 |- ( ( k + 1 ) e. _V -> [_ ( k + 1 ) / i ]_ ( d ^r i ) = ( d ^r ( k + 1 ) ) )
114107, 113ax-mp 5 . . . . . . . . . . . . . . . . . . . 20 |- [_ ( k + 1 ) / i ]_ ( d ^r i ) = ( d ^r ( k + 1 ) )
115106, 109, 1143sstr4g 3646 . . . . . . . . . . . . . . . . . . 19 |- ( k e. NN0 -> [_ ( k + 1 ) / i ]_ ( ( d ^r k ) o. ( d ^r 1 ) ) C_ [_ ( k + 1 ) / i ]_ ( d ^r i ) )
116 sbcssg 4085 . . . . . . . . . . . . . . . . . . . 20 |- ( ( k + 1 ) e. _V -> ( [. ( k + 1 ) / i ]. ( ( d ^r k ) o. ( d ^r 1 ) ) C_ ( d ^r i ) <-> [_ ( k + 1 ) / i ]_ ( ( d ^r k ) o. ( d ^r 1 ) ) C_ [_ ( k + 1 ) / i ]_ ( d ^r i ) ) )
117107, 116ax-mp 5 . . . . . . . . . . . . . . . . . . 19 |- ( [. ( k + 1 ) / i ]. ( ( d ^r k ) o. ( d ^r 1 ) ) C_ ( d ^r i ) <-> [_ ( k + 1 ) / i ]_ ( ( d ^r k ) o. ( d ^r 1 ) ) C_ [_ ( k + 1 ) / i ]_ ( d ^r i ) )
118115, 117sylibr 224 . . . . . . . . . . . . . . . . . 18 |- ( k e. NN0 -> [. ( k + 1 ) / i ]. ( ( d ^r k ) o. ( d ^r 1 ) ) C_ ( d ^r i ) )
119 sbcan 3478 . . . . . . . . . . . . . . . . . 18 |- ( [. ( k + 1 ) / i ]. ( i e. NN0 /\ ( ( d ^r k ) o. ( d ^r 1 ) ) C_ ( d ^r i ) ) <-> ( [. ( k + 1 ) / i ]. i e. NN0 /\ [. ( k + 1 ) / i ]. ( ( d ^r k ) o. ( d ^r 1 ) ) C_ ( d ^r i ) ) )
120104, 118, 119sylanbrc 698 . . . . . . . . . . . . . . . . 17 |- ( k e. NN0 -> [. ( k + 1 ) / i ]. ( i e. NN0 /\ ( ( d ^r k ) o. ( d ^r 1 ) ) C_ ( d ^r i ) ) )
121120spesbcd 3522 . . . . . . . . . . . . . . . 16 |- ( k e. NN0 -> E. i ( i e. NN0 /\ ( ( d ^r k ) o. ( d ^r 1 ) ) C_ ( d ^r i ) ) )
122 df-rex 2918 . . . . . . . . . . . . . . . 16 |- ( E. i e. NN0 ( ( d ^r k ) o. ( d ^r 1 ) ) C_ ( d ^r i ) <-> E. i ( i e. NN0 /\ ( ( d ^r k ) o. ( d ^r 1 ) ) C_ ( d ^r i ) ) )
123121, 122sylibr 224 . . . . . . . . . . . . . . 15 |- ( k e. NN0 -> E. i e. NN0 ( ( d ^r k ) o. ( d ^r 1 ) ) C_ ( d ^r i ) )
124101, 123mprg 2926 . . . . . . . . . . . . . 14 |- U_ k e. NN0 ( ( d ^r k ) o. ( d ^r 1 ) ) C_ U_ i e. NN0 ( d ^r i )
125100, 124eqsstri 3635 . . . . . . . . . . . . 13 |- ( U_ k e. NN0 ( d ^r k ) o. ( d ^r 1 ) ) C_ U_ i e. NN0 ( d ^r i )
126 oveq2 6658 . . . . . . . . . . . . . 14 |- ( i = k -> ( d ^r i ) = ( d ^r k ) )
127126cbviunv 4559 . . . . . . . . . . . . 13 |- U_ i e. NN0 ( d ^r i ) = U_ k e. NN0 ( d ^r k )
128125, 127sseqtri 3637 . . . . . . . . . . . 12 |- ( U_ k e. NN0 ( d ^r k ) o. ( d ^r 1 ) ) C_ U_ k e. NN0 ( d ^r k )
12999, 128unssi 3788 . . . . . . . . . . 11 |- ( ( U_ k e. NN0 ( d ^r k ) o. ( d ^r 0 ) ) u. ( U_ k e. NN0 ( d ^r k ) o. ( d ^r 1 ) ) ) C_ U_ k e. NN0 ( d ^r k )
13086, 129eqsstri 3635 . . . . . . . . . 10 |- ( U_ k e. NN0 ( d ^r k ) o. ( ( d ^r 0 ) u. ( d ^r 1 ) ) ) C_ U_ k e. NN0 ( d ^r k )
13185, 130syl6ss 3615 . . . . . . . . 9 |- ( ( ( ( d ^r 0 ) u. ( d ^r 1 ) ) ^r y ) C_ U_ k e. NN0 ( d ^r k ) -> ( ( ( ( d ^r 0 ) u. ( d ^r 1 ) ) ^r y ) o. ( ( d ^r 0 ) u. ( d ^r 1 ) ) ) C_ U_ k e. NN0 ( d ^r k ) )
132131adantl 482 . . . . . . . 8 |- ( ( y e. NN /\ ( ( ( d ^r 0 ) u. ( d ^r 1 ) ) ^r y ) C_ U_ k e. NN0 ( d ^r k ) ) -> ( ( ( ( d ^r 0 ) u. ( d ^r 1 ) ) ^r y ) o. ( ( d ^r 0 ) u. ( d ^r 1 ) ) ) C_ U_ k e. NN0 ( d ^r k ) )
13384, 132eqsstrd 3639 . . . . . . 7 |- ( ( y e. NN /\ ( ( ( d ^r 0 ) u. ( d ^r 1 ) ) ^r y ) C_ U_ k e. NN0 ( d ^r k ) ) -> ( ( ( d ^r 0 ) u. ( d ^r 1 ) ) ^r ( y + 1 ) ) C_ U_ k e. NN0 ( d ^r k ) )
134133ex 450 . . . . . 6 |- ( y e. NN -> ( ( ( ( d ^r 0 ) u. ( d ^r 1 ) ) ^r y ) C_ U_ k e. NN0 ( d ^r k ) -> ( ( ( d ^r 0 ) u. ( d ^r 1 ) ) ^r ( y + 1 ) ) C_ U_ k e. NN0 ( d ^r k ) ) )
13560, 62, 64, 66, 81, 134nnind 11038 . . . . 5 |- ( i e. NN -> ( ( ( d ^r 0 ) u. ( d ^r 1 ) ) ^r i ) C_ U_ k e. NN0 ( d ^r k ) )
13658, 135syl5eqss 3649 . . . 4 |- ( i e. NN -> ( U_ j e. { 0 , 1 } ( d ^r j ) ^r i ) C_ U_ k e. NN0 ( d ^r k ) )
13748, 136mprgbir 2927 . . 3 |- U_ i e. NN ( U_ j e. { 0 , 1 } ( d ^r j ) ^r i ) C_ U_ k e. NN0 ( d ^r k )
138 iuneq1 4534 . . . 4 |- ( NN0 = ( NN u. { 0 , 1 } ) -> U_ k e. NN0 ( d ^r k ) = U_ k e. ( NN u. { 0 , 1 } ) ( d ^r k ) )
13918, 138ax-mp 5 . . 3 |- U_ k e. NN0 ( d ^r k ) = U_ k e. ( NN u. { 0 , 1 } ) ( d ^r k )
140137, 139sseqtri 3637 . 2 |- U_ i e. NN ( U_ j e. { 0 , 1 } ( d ^r j ) ^r i ) C_ U_ k e. ( NN u. { 0 , 1 } ) ( d ^r k )
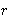1411, 2, 3, 4, 5, 18, 38, 47, 140comptiunov2i 37998 1 |- ( t+ o. r* ) = t*
Colors of variables: wff setvar class
Syntax hints:   <-> wb 196   /\ wa 384   = wceq 1483   E.wex 1704   e. wcel 1990   E.wrex 2913   _Vcvv 3200   [.wsbc 3435   [_csb 3533   u. cun 3572   C_ wss 3574   {csn 4177   {cpr 4179   U_ciun 4520   _I cid 5023   dom cdm 5114   ran crn 5115   |` cres 5116   o. ccom 5118  (class class class)co 6650   0cc0 9936   1c1 9937   + caddc 9939   NNcn 11020   NN0cn0 11292   t+ctcl 13724   t*crtcl 13725   ^r crelexp 13760   r*crcl 37964
This theorem was proved from axioms:  ax-mp 5  ax-1 6  ax-2 7  ax-3 8  ax-gen 1722  ax-4 1737  ax-5 1839  ax-6 1888  ax-7 1935  ax-8 1992  ax-9 1999  ax-10 2019  ax-11 2034  ax-12 2047  ax-13 2246  ax-ext 2602  ax-rep 4771  ax-sep 4781  ax-nul 4789  ax-pow 4843  ax-pr 4906  ax-un 6949  ax-cnex 9992  ax-resscn 9993  ax-1cn 9994  ax-icn 9995  ax-addcl 9996  ax-addrcl 9997  ax-mulcl 9998  ax-mulrcl 9999  ax-mulcom 10000  ax-addass 10001  ax-mulass 10002  ax-distr 10003  ax-i2m1 10004  ax-1ne0 10005  ax-1rid 10006  ax-rnegex 10007  ax-rrecex 10008  ax-cnre 10009  ax-pre-lttri 10010  ax-pre-lttrn 10011  ax-pre-ltadd 10012  ax-pre-mulgt0 10013
This theorem depends on definitions:  df-bi 197  df-or 385  df-an 386  df-3or 1038  df-3an 1039  df-tru 1486  df-fal 1489  df-ex 1705  df-nf 1710  df-sb 1881  df-eu 2474  df-mo 2475  df-clab 2609  df-cleq 2615  df-clel 2618  df-nfc 2753  df-ne 2795  df-nel 2898  df-ral 2917  df-rex 2918  df-reu 2919  df-rab 2921  df-v 3202  df-sbc 3436  df-csb 3534  df-dif 3577  df-un 3579  df-in 3581  df-ss 3588  df-pss 3590  df-nul 3916  df-if 4087  df-pw 4160  df-sn 4178  df-pr 4180  df-tp 4182  df-op 4184  df-uni 4437  df-int 4476  df-iun 4522  df-br 4654  df-opab 4713  df-mpt 4730  df-tr 4753  df-id 5024  df-eprel 5029  df-po 5035  df-so 5036  df-fr 5073  df-we 5075  df-xp 5120  df-rel 5121  df-cnv 5122  df-co 5123  df-dm 5124  df-rn 5125  df-res 5126  df-ima 5127  df-pred 5680  df-ord 5726  df-on 5727  df-lim 5728  df-suc 5729  df-iota 5851  df-fun 5890  df-fn 5891  df-f 5892  df-f1 5893  df-fo 5894  df-f1o 5895  df-fv 5896  df-riota 6611  df-ov 6653  df-oprab 6654  df-mpt2 6655  df-om 7066  df-2nd 7169  df-wrecs 7407  df-recs 7468  df-rdg 7506  df-er 7742  df-en 7956  df-dom 7957  df-sdom 7958  df-pnf 10076  df-mnf 10077  df-xr 10078  df-ltxr 10079  df-le 10080  df-sub 10268  df-neg 10269  df-nn 11021  df-2 11079  df-n0 11293  df-z 11378  df-uz 11688  df-seq 12802  df-trcl 13726  df-rtrcl 13727  df-relexp 13761  df-rcl 37965
This theorem is referenced by:  cortrclrcl  38035  cotrclrtrcl  38036  cortrclrtrcl  38037
  Copyright terms: Public domain W3C validator