MPE Home Metamath Proof Explorer < Previous   Next >
Nearby theorems
Mirrors  >  Home  >  MPE Home  >  Th. List  >  grur1 Structured version   Visualization version   Unicode version
Theorem grur1 9642
Description: A characterization of Grothendieck universes, part 2. (Contributed by Mario Carneiro, 24-Jun-2013.)
Hypothesis
Ref Expression
gruina.1 |- A = ( U i^i On )
Assertion
Ref Expression
grur1 |- ( ( U e. Univ /\ U e. U. ( R1 " On ) ) -> U = ( R1 ` A ) )
Proof of Theorem grur1
Dummy variables x y are mutually distinct and distinct from all other variables.
StepHypRef Expression
1 nss 3663 . . . . 5 |- ( -. U C_ ( R1 ` A ) <-> E. x ( x e. U /\ -. x e. ( R1 ` A ) ) )
2 fveq2 6191 . . . . . . . . . . . 12 |- ( y = x -> ( rank ` y ) = ( rank ` x ) )
32eqeq1d 2624 . . . . . . . . . . 11 |- ( y = x -> ( ( rank ` y ) = A <-> ( rank ` x ) = A ) )
43rspcev 3309 . . . . . . . . . 10 |- ( ( x e. U /\ ( rank ` x ) = A ) -> E. y e. U ( rank ` y ) = A )
54ex 450 . . . . . . . . 9 |- ( x e. U -> ( ( rank ` x ) = A -> E. y e. U ( rank ` y ) = A ) )
65ad2antrl 764 . . . . . . . 8 |- ( ( ( U e. Univ /\ U e. U. ( R1 " On ) ) /\ ( x e. U /\ -. x e. ( R1 ` A ) ) ) -> ( ( rank ` x ) = A -> E. y e. U ( rank ` y ) = A ) )
7 simplr 792 . . . . . . . . . . . 12 |- ( ( ( U e. Univ /\ U e. U. ( R1 " On ) ) /\ ( x e. U /\ -. x e. ( R1 ` A ) ) ) -> U e. U. ( R1 " On ) )
8 simprl 794 . . . . . . . . . . . 12 |- ( ( ( U e. Univ /\ U e. U. ( R1 " On ) ) /\ ( x e. U /\ -. x e. ( R1 ` A ) ) ) -> x e. U )
9 r1elssi 8668 . . . . . . . . . . . . 13 |- ( U e. U. ( R1 " On ) -> U C_ U. ( R1 " On ) )
109sseld 3602 . . . . . . . . . . . 12 |- ( U e. U. ( R1 " On ) -> ( x e. U -> x e. U. ( R1 " On ) ) )
117, 8, 10sylc 65 . . . . . . . . . . 11 |- ( ( ( U e. Univ /\ U e. U. ( R1 " On ) ) /\ ( x e. U /\ -. x e. ( R1 ` A ) ) ) -> x e. U. ( R1 " On ) )
12 tcrank 8747 . . . . . . . . . . 11 |- ( x e. U. ( R1 " On ) -> ( rank ` x ) = ( rank " ( TC ` x ) ) )
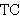1311, 12syl 17 . . . . . . . . . 10 |- ( ( ( U e. Univ /\ U e. U. ( R1 " On ) ) /\ ( x e. U /\ -. x e. ( R1 ` A ) ) ) -> ( rank ` x ) = ( rank " ( TC ` x ) ) )
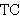1413eleq2d 2687 . . . . . . . . 9 |- ( ( ( U e. Univ /\ U e. U. ( R1 " On ) ) /\ ( x e. U /\ -. x e. ( R1 ` A ) ) ) -> ( A e. ( rank ` x ) <-> A e. ( rank " ( TC ` x ) ) ) )
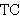15 gruelss 9616 . . . . . . . . . . . 12 |- ( ( U e. Univ /\ x e. U ) -> x C_ U )
16 grutr 9615 . . . . . . . . . . . . 13 |- ( U e. Univ -> Tr U )
1716adantr 481 . . . . . . . . . . . 12 |- ( ( U e. Univ /\ x e. U ) -> Tr U )
18 vex 3203 . . . . . . . . . . . . 13 |- x e. _V
19 tcmin 8617 . . . . . . . . . . . . 13 |- ( x e. _V -> ( ( x C_ U /\ Tr U ) -> ( TC ` x ) C_ U ) )
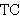
2018, 19ax-mp 5 . . . . . . . . . . . 12 |- ( ( x C_ U /\ Tr U ) -> ( TC ` x ) C_ U )
2115, 17, 20syl2anc 693 . . . . . . . . . . 11 |- ( ( U e. Univ /\ x e. U ) -> ( TC ` x ) C_ U )
22 rankf 8657 . . . . . . . . . . . . 13 |- rank : U. ( R1 " On ) --> On
23 ffun 6048 . . . . . . . . . . . . 13 |- ( rank : U. ( R1 " On ) --> On -> Fun rank )
2422, 23ax-mp 5 . . . . . . . . . . . 12 |- Fun rank
25 fvelima 6248 . . . . . . . . . . . 12 |- ( ( Fun rank /\ A e. ( rank " ( TC ` x ) ) ) -> E. y e. ( TC ` x ) ( rank ` y ) = A )
2624, 25mpan 706 . . . . . . . . . . 11 |- ( A e. ( rank " ( TC ` x ) ) -> E. y e. ( TC ` x ) ( rank ` y ) = A )
27 ssrexv 3667 . . . . . . . . . . 11 |- ( ( TC ` x ) C_ U -> ( E. y e. ( TC ` x ) ( rank ` y ) = A -> E. y e. U ( rank ` y ) = A ) )
2821, 26, 27syl2im 40 . . . . . . . . . 10 |- ( ( U e. Univ /\ x e. U ) -> ( A e. ( rank " ( TC ` x ) ) -> E. y e. U ( rank ` y ) = A ) )
2928ad2ant2r 783 . . . . . . . . 9 |- ( ( ( U e. Univ /\ U e. U. ( R1 " On ) ) /\ ( x e. U /\ -. x e. ( R1 ` A ) ) ) -> ( A e. ( rank " ( TC ` x ) ) -> E. y e. U ( rank ` y ) = A ) )
3014, 29sylbid 230 . . . . . . . 8 |- ( ( ( U e. Univ /\ U e. U. ( R1 " On ) ) /\ ( x e. U /\ -. x e. ( R1 ` A ) ) ) -> ( A e. ( rank ` x ) -> E. y e. U ( rank ` y ) = A ) )
31 simprr 796 . . . . . . . . . 10 |- ( ( ( U e. Univ /\ U e. U. ( R1 " On ) ) /\ ( x e. U /\ -. x e. ( R1 ` A ) ) ) -> -. x e. ( R1 ` A ) )
32 ne0i 3921 . . . . . . . . . . . . . . 15 |- ( x e. U -> U =/= (/) )
33 gruina.1 . . . . . . . . . . . . . . . 16 |- A = ( U i^i On )
3433gruina 9640 . . . . . . . . . . . . . . 15 |- ( ( U e. Univ /\ U =/= (/) ) -> A e. Inacc )
3532, 34sylan2 491 . . . . . . . . . . . . . 14 |- ( ( U e. Univ /\ x e. U ) -> A e. Inacc )
36 inawina 9512 . . . . . . . . . . . . . 14 |- ( A e. Inacc -> A e. InaccW )
37 winaon 9510 . . . . . . . . . . . . . 14 |- ( A e. InaccW -> A e. On )
3835, 36, 373syl 18 . . . . . . . . . . . . 13 |- ( ( U e. Univ /\ x e. U ) -> A e. On )
39 r1fnon 8630 . . . . . . . . . . . . . 14 |- R1 Fn On
40 fndm 5990 . . . . . . . . . . . . . 14 |- ( R1 Fn On -> dom R1 = On )
4139, 40ax-mp 5 . . . . . . . . . . . . 13 |- dom R1 = On
4238, 41syl6eleqr 2712 . . . . . . . . . . . 12 |- ( ( U e. Univ /\ x e. U ) -> A e. dom R1 )
4342ad2ant2r 783 . . . . . . . . . . 11 |- ( ( ( U e. Univ /\ U e. U. ( R1 " On ) ) /\ ( x e. U /\ -. x e. ( R1 ` A ) ) ) -> A e. dom R1 )
44 rankr1ag 8665 . . . . . . . . . . 11 |- ( ( x e. U. ( R1 " On ) /\ A e. dom R1 ) -> ( x e. ( R1 ` A ) <-> ( rank ` x ) e. A ) )
4511, 43, 44syl2anc 693 . . . . . . . . . 10 |- ( ( ( U e. Univ /\ U e. U. ( R1 " On ) ) /\ ( x e. U /\ -. x e. ( R1 ` A ) ) ) -> ( x e. ( R1 ` A ) <-> ( rank ` x ) e. A ) )
4631, 45mtbid 314 . . . . . . . . 9 |- ( ( ( U e. Univ /\ U e. U. ( R1 " On ) ) /\ ( x e. U /\ -. x e. ( R1 ` A ) ) ) -> -. ( rank ` x ) e. A )
47 rankon 8658 . . . . . . . . . . . . 13 |- ( rank ` x ) e. On
48 eloni 5733 . . . . . . . . . . . . . 14 |- ( ( rank ` x ) e. On -> Ord ( rank ` x ) )
49 eloni 5733 . . . . . . . . . . . . . 14 |- ( A e. On -> Ord A )
50 ordtri3or 5755 . . . . . . . . . . . . . 14 |- ( ( Ord ( rank ` x ) /\ Ord A ) -> ( ( rank ` x ) e. A \/ ( rank ` x ) = A \/ A e. ( rank ` x ) ) )
5148, 49, 50syl2an 494 . . . . . . . . . . . . 13 |- ( ( ( rank ` x ) e. On /\ A e. On ) -> ( ( rank ` x ) e. A \/ ( rank ` x ) = A \/ A e. ( rank ` x ) ) )
5247, 38, 51sylancr 695 . . . . . . . . . . . 12 |- ( ( U e. Univ /\ x e. U ) -> ( ( rank ` x ) e. A \/ ( rank ` x ) = A \/ A e. ( rank ` x ) ) )
53 3orass 1040 . . . . . . . . . . . 12 |- ( ( ( rank ` x ) e. A \/ ( rank ` x ) = A \/ A e. ( rank ` x ) ) <-> ( ( rank ` x ) e. A \/ ( ( rank ` x ) = A \/ A e. ( rank ` x ) ) ) )
5452, 53sylib 208 . . . . . . . . . . 11 |- ( ( U e. Univ /\ x e. U ) -> ( ( rank ` x ) e. A \/ ( ( rank ` x ) = A \/ A e. ( rank ` x ) ) ) )
5554ord 392 . . . . . . . . . 10 |- ( ( U e. Univ /\ x e. U ) -> ( -. ( rank ` x ) e. A -> ( ( rank ` x ) = A \/ A e. ( rank ` x ) ) ) )
5655ad2ant2r 783 . . . . . . . . 9 |- ( ( ( U e. Univ /\ U e. U. ( R1 " On ) ) /\ ( x e. U /\ -. x e. ( R1 ` A ) ) ) -> ( -. ( rank ` x ) e. A -> ( ( rank ` x ) = A \/ A e. ( rank ` x ) ) ) )
5746, 56mpd 15 . . . . . . . 8 |- ( ( ( U e. Univ /\ U e. U. ( R1 " On ) ) /\ ( x e. U /\ -. x e. ( R1 ` A ) ) ) -> ( ( rank ` x ) = A \/ A e. ( rank ` x ) ) )
586, 30, 57mpjaod 396 . . . . . . 7 |- ( ( ( U e. Univ /\ U e. U. ( R1 " On ) ) /\ ( x e. U /\ -. x e. ( R1 ` A ) ) ) -> E. y e. U ( rank ` y ) = A )
5958ex 450 . . . . . 6 |- ( ( U e. Univ /\ U e. U. ( R1 " On ) ) -> ( ( x e. U /\ -. x e. ( R1 ` A ) ) -> E. y e. U ( rank ` y ) = A ) )
6059exlimdv 1861 . . . . 5 |- ( ( U e. Univ /\ U e. U. ( R1 " On ) ) -> ( E. x ( x e. U /\ -. x e. ( R1 ` A ) ) -> E. y e. U ( rank ` y ) = A ) )
611, 60syl5bi 232 . . . 4 |- ( ( U e. Univ /\ U e. U. ( R1 " On ) ) -> ( -. U C_ ( R1 ` A ) -> E. y e. U ( rank ` y ) = A ) )
62 simpll 790 . . . . . . 7 |- ( ( ( U e. Univ /\ U e. U. ( R1 " On ) ) /\ ( y e. U /\ ( rank ` y ) = A ) ) -> U e. Univ )
63 ne0i 3921 . . . . . . . . . 10 |- ( y e. U -> U =/= (/) )
6463, 34sylan2 491 . . . . . . . . 9 |- ( ( U e. Univ /\ y e. U ) -> A e. Inacc )
6564ad2ant2r 783 . . . . . . . 8 |- ( ( ( U e. Univ /\ U e. U. ( R1 " On ) ) /\ ( y e. U /\ ( rank ` y ) = A ) ) -> A e. Inacc )
6665, 36, 373syl 18 . . . . . . 7 |- ( ( ( U e. Univ /\ U e. U. ( R1 " On ) ) /\ ( y e. U /\ ( rank ` y ) = A ) ) -> A e. On )
67 simprl 794 . . . . . . 7 |- ( ( ( U e. Univ /\ U e. U. ( R1 " On ) ) /\ ( y e. U /\ ( rank ` y ) = A ) ) -> y e. U )
68 fveq2 6191 . . . . . . . . . 10 |- ( ( rank ` y ) = A -> ( cf ` ( rank ` y ) ) = ( cf ` A ) )
6968ad2antll 765 . . . . . . . . 9 |- ( ( ( U e. Univ /\ U e. U. ( R1 " On ) ) /\ ( y e. U /\ ( rank ` y ) = A ) ) -> ( cf ` ( rank ` y ) ) = ( cf ` A ) )
70 elina 9509 . . . . . . . . . . 11 |- ( A e. Inacc <-> ( A =/= (/) /\ ( cf ` A ) = A /\ A. x e. A ~P x ~< A ) )
7170simp2bi 1077 . . . . . . . . . 10 |- ( A e. Inacc -> ( cf ` A ) = A )
7265, 71syl 17 . . . . . . . . 9 |- ( ( ( U e. Univ /\ U e. U. ( R1 " On ) ) /\ ( y e. U /\ ( rank ` y ) = A ) ) -> ( cf ` A ) = A )
7369, 72eqtrd 2656 . . . . . . . 8 |- ( ( ( U e. Univ /\ U e. U. ( R1 " On ) ) /\ ( y e. U /\ ( rank ` y ) = A ) ) -> ( cf ` ( rank ` y ) ) = A )
74 rankcf 9599 . . . . . . . . 9 |- -. y ~< ( cf ` ( rank ` y ) )
75 fvex 6201 . . . . . . . . . 10 |- ( cf ` ( rank ` y ) ) e. _V
76 vex 3203 . . . . . . . . . 10 |- y e. _V
77 domtri 9378 . . . . . . . . . 10 |- ( ( ( cf ` ( rank ` y ) ) e. _V /\ y e. _V ) -> ( ( cf ` ( rank ` y ) ) ~<_ y <-> -. y ~< ( cf ` ( rank ` y ) ) ) )
7875, 76, 77mp2an 708 . . . . . . . . 9 |- ( ( cf ` ( rank ` y ) ) ~<_ y <-> -. y ~< ( cf ` ( rank ` y ) ) )
7974, 78mpbir 221 . . . . . . . 8 |- ( cf ` ( rank ` y ) ) ~<_ y
8073, 79syl6eqbrr 4693 . . . . . . 7 |- ( ( ( U e. Univ /\ U e. U. ( R1 " On ) ) /\ ( y e. U /\ ( rank ` y ) = A ) ) -> A ~<_ y )
81 grudomon 9639 . . . . . . 7 |- ( ( U e. Univ /\ A e. On /\ ( y e. U /\ A ~<_ y ) ) -> A e. U )
8262, 66, 67, 80, 81syl112anc 1330 . . . . . 6 |- ( ( ( U e. Univ /\ U e. U. ( R1 " On ) ) /\ ( y e. U /\ ( rank ` y ) = A ) ) -> A e. U )
83 elin 3796 . . . . . . . . 9 |- ( A e. ( U i^i On ) <-> ( A e. U /\ A e. On ) )
8483biimpri 218 . . . . . . . 8 |- ( ( A e. U /\ A e. On ) -> A e. ( U i^i On ) )
8584, 33syl6eleqr 2712 . . . . . . 7 |- ( ( A e. U /\ A e. On ) -> A e. A )
86 ordirr 5741 . . . . . . . . 9 |- ( Ord A -> -. A e. A )
8749, 86syl 17 . . . . . . . 8 |- ( A e. On -> -. A e. A )
8887adantl 482 . . . . . . 7 |- ( ( A e. U /\ A e. On ) -> -. A e. A )
8985, 88pm2.21dd 186 . . . . . 6 |- ( ( A e. U /\ A e. On ) -> U C_ ( R1 ` A ) )
9082, 66, 89syl2anc 693 . . . . 5 |- ( ( ( U e. Univ /\ U e. U. ( R1 " On ) ) /\ ( y e. U /\ ( rank ` y ) = A ) ) -> U C_ ( R1 ` A ) )
9190rexlimdvaa 3032 . . . 4 |- ( ( U e. Univ /\ U e. U. ( R1 " On ) ) -> ( E. y e. U ( rank ` y ) = A -> U C_ ( R1 ` A ) ) )
9261, 91syld 47 . . 3 |- ( ( U e. Univ /\ U e. U. ( R1 " On ) ) -> ( -. U C_ ( R1 ` A ) -> U C_ ( R1 ` A ) ) )
9392pm2.18d 124 . 2 |- ( ( U e. Univ /\ U e. U. ( R1 " On ) ) -> U C_ ( R1 ` A ) )
9433grur1a 9641 . . 3 |- ( U e. Univ -> ( R1 ` A ) C_ U )
9594adantr 481 . 2 |- ( ( U e. Univ /\ U e. U. ( R1 " On ) ) -> ( R1 ` A ) C_ U )
9693, 95eqssd 3620 1 |- ( ( U e. Univ /\ U e. U. ( R1 " On ) ) -> U = ( R1 ` A ) )
Colors of variables: wff setvar class
Syntax hints:   -. wn 3   -> wi 4   <-> wb 196   \/ wo 383   /\ wa 384   \/ w3o 1036   = wceq 1483   E.wex 1704   e. wcel 1990   =/= wne 2794   A.wral 2912   E.wrex 2913   _Vcvv 3200   i^i cin 3573   C_ wss 3574   (/)c0 3915   ~Pcpw 4158   U.cuni 4436   class class class wbr 4653   Tr wtr 4752   dom cdm 5114   "cima 5117   Ord word 5722   Oncon0 5723   Fun wfun 5882   Fn wfn 5883   -->wf 5884   ` cfv 5888   ~<_ cdom 7953   ~< csdm 7954   TCctc 8612   R1cr1 8625   rankcrnk 8626   cfccf 8763   InaccWcwina 9504   Inacccina 9505   Univcgru 9612
This theorem was proved from axioms:  ax-mp 5  ax-1 6  ax-2 7  ax-3 8  ax-gen 1722  ax-4 1737  ax-5 1839  ax-6 1888  ax-7 1935  ax-8 1992  ax-9 1999  ax-10 2019  ax-11 2034  ax-12 2047  ax-13 2246  ax-ext 2602  ax-rep 4771  ax-sep 4781  ax-nul 4789  ax-pow 4843  ax-pr 4906  ax-un 6949  ax-inf2 8538  ax-ac2 9285
This theorem depends on definitions:  df-bi 197  df-or 385  df-an 386  df-3or 1038  df-3an 1039  df-tru 1486  df-ex 1705  df-nf 1710  df-sb 1881  df-eu 2474  df-mo 2475  df-clab 2609  df-cleq 2615  df-clel 2618  df-nfc 2753  df-ne 2795  df-ral 2917  df-rex 2918  df-reu 2919  df-rmo 2920  df-rab 2921  df-v 3202  df-sbc 3436  df-csb 3534  df-dif 3577  df-un 3579  df-in 3581  df-ss 3588  df-pss 3590  df-nul 3916  df-if 4087  df-pw 4160  df-sn 4178  df-pr 4180  df-tp 4182  df-op 4184  df-uni 4437  df-int 4476  df-iun 4522  df-iin 4523  df-br 4654  df-opab 4713  df-mpt 4730  df-tr 4753  df-id 5024  df-eprel 5029  df-po 5035  df-so 5036  df-fr 5073  df-se 5074  df-we 5075  df-xp 5120  df-rel 5121  df-cnv 5122  df-co 5123  df-dm 5124  df-rn 5125  df-res 5126  df-ima 5127  df-pred 5680  df-ord 5726  df-on 5727  df-lim 5728  df-suc 5729  df-iota 5851  df-fun 5890  df-fn 5891  df-f 5892  df-f1 5893  df-fo 5894  df-f1o 5895  df-fv 5896  df-isom 5897  df-riota 6611  df-ov 6653  df-oprab 6654  df-mpt2 6655  df-om 7066  df-1st 7168  df-2nd 7169  df-wrecs 7407  df-recs 7468  df-rdg 7506  df-1o 7560  df-er 7742  df-map 7859  df-en 7956  df-dom 7957  df-sdom 7958  df-fin 7959  df-tc 8613  df-r1 8627  df-rank 8628  df-card 8765  df-cf 8767  df-acn 8768  df-ac 8939  df-wina 9506  df-ina 9507  df-gru 9613
This theorem is referenced by:  grutsk  9644  bj-grur1  33023
  Copyright terms: Public domain W3C validator