| Step | Hyp | Ref
| Expression |
|---|
| 1 | | fveq1 6190 |
. . . . . . . . . 10
                  |
| 2 | 1 | fveq2d 6195 |
. . . . . . . . 9
                          |
| 3 | 2 | breq1d 4663 |
. . . . . . . 8
                
 
             |
| 4 | 3 | cbvralv 3171 |
. . . . . . 7
    
                             |
| 5 | | breq2 4657 |
. . . . . . . 8
                
 
             |
| 6 | 5 | ralbidv 2986 |
. . . . . . 7
        
             
   
             |
| 7 | 4, 6 | syl5bb 272 |
. . . . . 6
        
             
   
             |
| 8 | 7 | cbvrexv 3172 |
. . . . 5
        
                                 |
| 9 | | fveq2 6191 |
. . . . . . . 8
                  |
| 10 | 9 | fveq2d 6195 |
. . . . . . 7
                          |
| 11 | 10 | breq1d 4663 |
. . . . . 6
                
 
             |
| 12 | 11 | rexralbidv 3058 |
. . . . 5
        
                 
                     |
| 13 | 8, 12 | syl5bb 272 |
. . . 4
        
                 
                     |
| 14 | 13 | cbvralv 3171 |
. . 3
    
   
    
                  
    
            |
| 15 | | ubth.1 |
. . . . . 6
    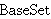    |
| 16 | | ubth.2 |
. . . . . 6
     CV CV   |
| 17 | | ubthlem.3 |
. . . . . 6
    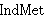    |
| 18 | | ubthlem.4 |
. . . . . 6
        |
| 19 | | ubthlem.5 |
. . . . . 6
   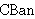 |
| 20 | | ubthlem.6 |
. . . . . 6
    |
| 21 | | ubthlem.7 |
. . . . . . 7
     
  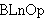    |
| 22 | 21 | adantr 481 |
. . . . . 6
    
   
                    
    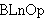    |
| 23 | | simpr 477 |
. . . . . . 7
    
   
                    
   
                    |
| 24 | 23, 14 | sylib 208 |
. . . . . 6
    
   
                    
   
                    |
| 25 | | fveq1 6190 |
. . . . . . . . . . . . 13
                  |
| 26 | 25 | fveq2d 6195 |
. . . . . . . . . . . 12
                          |
| 27 | 26 | breq1d 4663 |
. . . . . . . . . . 11
                
 
             |
| 28 | 27 | cbvralv 3171 |
. . . . . . . . . 10
    
                             |
| 29 | | fveq2 6191 |
. . . . . . . . . . . . 13
                  |
| 30 | 29 | fveq2d 6195 |
. . . . . . . . . . . 12
                          |
| 31 | 30 | breq1d 4663 |
. . . . . . . . . . 11
                
 
             |
| 32 | 31 | ralbidv 2986 |
. . . . . . . . . 10
        
             
   
             |
| 33 | 28, 32 | syl5bb 272 |
. . . . . . . . 9
        
             
   
             |
| 34 | 33 | cbvrabv 3199 |
. . . . . . . 8
        
            
       
              |
| 35 | | breq2 4657 |
. . . . . . . . . 10
                
 
             |
| 36 | 35 | ralbidv 2986 |
. . . . . . . . 9
        
             
   
             |
| 37 | 36 | rabbidv 3189 |
. . . . . . . 8
             
            
       
               |
| 38 | 34, 37 | syl5eq 2668 |
. . . . . . 7
             
            
       
               |
| 39 | 38 | cbvmptv 4750 |
. . . . . 6
             
                          
               |
| 40 | 15, 16, 17, 18, 19, 20, 22, 24, 39 | ubthlem1 27726 |
. . . . 5
    
   
                    
                                       
                  |
| 41 | 21 | ad3antrrr 766 |
. . . . . . . . 9
             
    
            
                                           
                        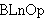    |
| 42 | 24 | ad2antrr 762 |
. . . . . . . . 9
             
    
            
                                           
                     
   
                  |
| 43 | | simplrl 800 |
. . . . . . . . 9
             
    
            
                                           
                     
  |
| 44 | | simplrr 801 |
. . . . . . . . 9
             
    
            
                                           
                        |
| 45 | | simprl 794 |
. . . . . . . . 9
             
    
            
                                           
                        |
| 46 | | simprr 796 |
. . . . . . . . 9
             
    
            
                                           
                                               
                  |
| 47 | 15, 16, 17, 18, 19, 20, 41, 42, 39, 43, 44, 45, 46 | ubthlem2 27727 |
. . . . . . . 8
             
    
            
                                           
                     
                   |
| 48 | 47 | expr 643 |
. . . . . . 7
             
    
            
            
                                                   
                    |
| 49 | 48 | rexlimdva 3031 |
. . . . . 6
        
   
    
            
                                           
                 
                      |
| 50 | 49 | rexlimdvva 3038 |
. . . . 5
    
   
                    
   
    
                                                   
                    |
| 51 | 40, 50 | mpd 15 |
. . . 4
    
   
                    
                     |
| 52 | 51 | ex 450 |
. . 3
                                                   |
| 53 | 14, 52 | syl5bir 233 |
. 2
                                                   |
| 54 | | simpr 477 |
. . . . . 6
    
   
     |
| 55 | | bnnv 27722 |
. . . . . . . 8
    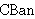
     |
| 56 | 19, 55 | ax-mp 5 |
. . . . . . 7
    |
| 57 | | eqid 2622 |
. . . . . . . 8
   CV CV      CV CV   |
| 58 | 15, 57 | nvcl 27516 |
. . . . . . 7
               CV CV         |
| 59 | 56, 58 | mpan 706 |
. . . . . 6
         CV CV         |
| 60 | | remulcl 10021 |
. . . . . 6
          CV CV                CV CV          |
| 61 | 54, 59, 60 | syl2an 494 |
. . . . 5
                      CV CV          |
| 62 | 21 | sselda 3603 |
. . . . . . . . . . . . 13
    
         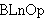    |
| 63 | 62 | adantlr 751 |
. . . . . . . . . . . 12
                    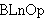    |
| 64 | 63 | ad2ant2r 783 |
. . . . . . . . . . 11
        
   
   
   
                    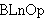    |
| 65 | | eqid 2622 |
. . . . . . . . . . . . 13
  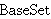      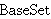    |
| 66 | | eqid 2622 |
. . . . . . . . . . . . 13
   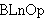      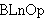
  |
| 67 | 15, 65, 66 | blof 27640 |
. . . . . . . . . . . 12
          
   
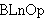    
     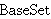     |
| 68 | 56, 20, 67 | mp3an12 1414 |
. . . . . . . . . . 11
      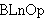   
     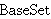     |
| 69 | 64, 68 | syl 17 |
. . . . . . . . . 10
        
   
   
   
                     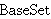     |
| 70 | | simplr 792 |
. . . . . . . . . 10
        
   
   
   
                 
  |
| 71 | 69, 70 | ffvelrnd 6360 |
. . . . . . . . 9
        
   
   
   
                       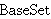     |
| 72 | 65, 16 | nvcl 27516 |
. . . . . . . . . 10
              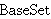     
            |
| 73 | 20, 72 | mpan 706 |
. . . . . . . . 9
         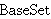    
            |
| 74 | 71, 73 | syl 17 |
. . . . . . . 8
        
   
   
   
                            |
| 75 | | eqid 2622 |
. . . . . . . . . . . . 13
              |
| 76 | 15, 65, 75 | nmoxr 27621 |
. . . . . . . . . . . 12
          
     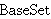     
             |
| 77 | 56, 20, 76 | mp3an12 1414 |
. . . . . . . . . . 11
       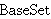                  |
| 78 | 69, 77 | syl 17 |
. . . . . . . . . 10
        
   
   
   
                             |
| 79 | | simpllr 799 |
. . . . . . . . . 10
        
   
   
   
                    |
| 80 | 15, 65, 75 | nmogtmnf 27625 |
. . . . . . . . . . . 12
          
     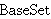     
             |
| 81 | 56, 20, 80 | mp3an12 1414 |
. . . . . . . . . . 11
       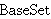                  |
| 82 | 69, 81 | syl 17 |
. . . . . . . . . 10
        
   
   
   
                             |
| 83 | | simprr 796 |
. . . . . . . . . 10
        
   
   
   
                          
  |
| 84 | | xrre 12000 |
. . . . . . . . . 10
                                              
   
             |
| 85 | 78, 79, 82, 83, 84 | syl22anc 1327 |
. . . . . . . . 9
        
   
   
   
                             |
| 86 | 59 | ad2antlr 763 |
. . . . . . . . 9
        
   
   
   
                   CV CV         |
| 87 | | remulcl 10021 |
. . . . . . . . 9
                   CV CV                         CV CV          |
| 88 | 85, 86, 87 | syl2anc 693 |
. . . . . . . 8
        
   
   
   
                               CV CV          |
| 89 | 61 | adantr 481 |
. . . . . . . 8
        
   
   
   
                      CV CV          |
| 90 | 15, 57, 16, 75, 66, 56, 20 | nmblolbi 27655 |
. . . . . . . . 9
       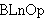                                  CV CV        |
| 91 | 64, 70, 90 | syl2anc 693 |
. . . . . . . 8
        
   
   
   
                         
               CV CV        |
| 92 | 15, 57 | nvge0 27528 |
. . . . . . . . . . . 12
                 CV CV       |
| 93 | 56, 92 | mpan 706 |
. . . . . . . . . . 11
           CV CV       |
| 94 | 59, 93 | jca 554 |
. . . . . . . . . 10
          CV CV              CV CV        |
| 95 | 94 | ad2antlr 763 |
. . . . . . . . 9
        
   
   
   
                    CV CV              CV CV        |
| 96 | | lemul1a 10877 |
. . . . . . . . 9
                         CV CV              CV CV                   
                  CV CV              CV CV        |
| 97 | 85, 79, 95, 83, 96 | syl31anc 1329 |
. . . . . . . 8
        
   
   
   
                               CV CV              CV CV        |
| 98 | 74, 88, 89, 91, 97 | letrd 10194 |
. . . . . . 7
        
   
   
   
                         
      CV CV        |
| 99 | 98 | expr 643 |
. . . . . 6
        
   
   
                
                  CV CV         |
| 100 | 99 | ralimdva 2962 |
. . . . 5
                  
            
                      CV CV         |
| 101 | | breq2 4657 |
. . . . . . 7
          CV CV       
                             CV CV         |
| 102 | 101 | ralbidv 2986 |
. . . . . 6
          CV CV       
   
                                 CV CV         |
| 103 | 102 | rspcev 3309 |
. . . . 5
         CV CV             
                CV CV                             |
| 104 | 61, 100, 103 | syl6an 568 |
. . . 4
                  
            
        
              |
| 105 | 104 | ralrimdva 2969 |
. . 3
    
   
    
             
   
                     |
| 106 | 105 | rexlimdva 3031 |
. 2
                               
                   |
| 107 | 53, 106 | impbid 202 |
1
                                   
               |