| Step | Hyp | Ref
| Expression |
|---|
| 1 | | noel 3919 |
. . . 4
     |
| 2 | | psgnunilem2.id |
. . . . . . . 8
       g g      
   |
| 3 | 2 | difeq1d 3727 |
. . . . . . 7
        g g                 |
| 4 | 3 | dmeqd 5326 |
. . . . . 6
         g g      
    
   
  |
| 5 | | resss 5422 |
. . . . . . . . 9
        |
| 6 | | ssdif0 3942 |
. . . . . . . . 9
    
              
  |
| 7 | 5, 6 | mpbi 220 |
. . . . . . . 8
    
   
   |
| 8 | 7 | dmeqi 5325 |
. . . . . . 7
              |
| 9 | | dm0 5339 |
. . . . . . 7
     |
| 10 | 8, 9 | eqtri 2644 |
. . . . . 6
             |
| 11 | 4, 10 | syl6eq 2672 |
. . . . 5
         g g      
  |
| 12 | 11 | eleq2d 2687 |
. . . 4
            g g      
     |
| 13 | 1, 12 | mtbiri 317 |
. . 3
            g g       |
| 14 | | psgnunilem2.d |
. . . . . . . . 9
        |
| 15 | | psgnunilem2.g |
. . . . . . . . . 10
        |
| 16 | 15 | symggrp 17820 |
. . . . . . . . 9
          |
| 17 | | grpmnd 17429 |
. . . . . . . . 9
          |
| 18 | 14, 16, 17 | 3syl 18 |
. . . . . . . 8
        |
| 19 | | psgnunilem2.t |
. . . . . . . . . . . 12
     pmTrsp pmTrsp   |
| 20 | | eqid 2622 |
. . . . . . . . . . . 12
            |
| 21 | 19, 15, 20 | symgtrf 17889 |
. . . . . . . . . . 11
        |
| 22 | | sswrd 13313 |
. . . . . . . . . . 11
          Word
Word   Word Word       |
| 23 | 21, 22 | mp1i 13 |
. . . . . . . . . 10
    Word Word   Word
Word       |
| 24 | | psgnunilem2.w |
. . . . . . . . . 10
      Word Word   |
| 25 | 23, 24 | sseldd 3604 |
. . . . . . . . 9
      Word Word       |
| 26 | | swrdcl 13419 |
. . . . . . . . 9
    Word Word      
  substr substr        Word Word       |
| 27 | 25, 26 | syl 17 |
. . . . . . . 8
      substr substr        Word Word       |
| 28 | 20 | gsumwcl 17377 |
. . . . . . . 8
         substr
substr        Word Word           g g   substr substr               |
| 29 | 18, 27, 28 | syl2anc 693 |
. . . . . . 7
       g g   substr substr               |
| 30 | 15, 20 | symgbasf1o 17803 |
. . . . . . 7
     g g   substr substr              
   g g   substr substr             |
| 31 | 29, 30 | syl 17 |
. . . . . 6
       g g   substr substr             |
| 32 | 31 | adantr 481 |
. . . . 5
    
            g g   substr substr             |
| 33 | | wrdf 13310 |
. . . . . . . . . 10
    Word Word       ..^ ..^         |
| 34 | 24, 33 | syl 17 |
. . . . . . . . 9
        ..^ ..^         |
| 35 | | psgnunilem2.ix |
. . . . . . . . . 10
        ..^ ..^   |
| 36 | | psgnunilem2.l |
. . . . . . . . . . 11
            |
| 37 | 36 | oveq2d 6666 |
. . . . . . . . . 10
      ..^ ..^         ..^ ..^   |
| 38 | 35, 37 | eleqtrrd 2704 |
. . . . . . . . 9
        ..^ ..^       |
| 39 | 34, 38 | ffvelrnd 6360 |
. . . . . . . 8
            |
| 40 | 21, 39 | sseldi 3601 |
. . . . . . 7
                |
| 41 | 15, 20 | symgbasf1o 17803 |
. . . . . . 7
             
          |
| 42 | 40, 41 | syl 17 |
. . . . . 6
              |
| 43 | 42 | adantr 481 |
. . . . 5
    
                   |
| 44 | 15, 20 | symgsssg 17887 |
. . . . . . . . . . . 12
                  
             SubGrp SubGrp    |
| 45 | | subgsubm 17616 |
. . . . . . . . . . . 12
                            SubGrp SubGrp   
            
             SubMnd SubMnd    |
| 46 | 14, 44, 45 | 3syl 18 |
. . . . . . . . . . 11
                  
           SubMnd SubMnd    |
| 47 | 46 | adantr 481 |
. . . . . . . . . 10
    
                     
             SubMnd SubMnd    |
| 48 | | fzossfz 12488 |
. . . . . . . . . . . . . . . . . . . . 21
   ..^ ..^        |
| 49 | 48, 35 | sseldi 3601 |
. . . . . . . . . . . . . . . . . . . 20
            |
| 50 | | elfzuz3 12339 |
. . . . . . . . . . . . . . . . . . . 20
                  |
| 51 | 49, 50 | syl 17 |
. . . . . . . . . . . . . . . . . . 19
            |
| 52 | 36, 51 | eqeltrd 2701 |
. . . . . . . . . . . . . . . . . 18
                |
| 53 | | fzoss2 12496 |
. . . . . . . . . . . . . . . . . 18
                ..^ ..^     ..^ ..^       |
| 54 | 52, 53 | syl 17 |
. . . . . . . . . . . . . . . . 17
      ..^ ..^     ..^ ..^       |
| 55 | 54 | sselda 3603 |
. . . . . . . . . . . . . . . 16
    
    ..^ ..^        ..^ ..^       |
| 56 | 34 | ffvelrnda 6359 |
. . . . . . . . . . . . . . . . 17
    
    ..^ ..^                |
| 57 | 21, 56 | sseldi 3601 |
. . . . . . . . . . . . . . . 16
    
    ..^ ..^                    |
| 58 | 55, 57 | syldan 487 |
. . . . . . . . . . . . . . 15
    
    ..^ ..^                |
| 59 | | psgnunilem2.al |
. . . . . . . . . . . . . . . . 17
         ..^ ..^            
   |
| 60 | | fveq2 6191 |
. . . . . . . . . . . . . . . . . . . . . 22
                  |
| 61 | 60 | difeq1d 3727 |
. . . . . . . . . . . . . . . . . . . . 21
            
             |
| 62 | 61 | dmeqd 5326 |
. . . . . . . . . . . . . . . . . . . 20
                
           |
| 63 | 62 | eleq2d 2687 |
. . . . . . . . . . . . . . . . . . 19
        
          
              |
| 64 | 63 | notbid 308 |
. . . . . . . . . . . . . . . . . 18
        
                           |
| 65 | 64 | cbvralv 3171 |
. . . . . . . . . . . . . . . . 17
    
  ..^ ..^              
      ..^ ..^            
   |
| 66 | 59, 65 | sylib 208 |
. . . . . . . . . . . . . . . 16
         ..^ ..^            
   |
| 67 | 66 | r19.21bi 2932 |
. . . . . . . . . . . . . . 15
    
    ..^ ..^    
             |
| 68 | | difeq1 3721 |
. . . . . . . . . . . . . . . . . . 19
            
             |
| 69 | 68 | dmeqd 5326 |
. . . . . . . . . . . . . . . . . 18
                
           |
| 70 | 69 | sseq1d 3632 |
. . . . . . . . . . . . . . . . 17
                         
            
       |
| 71 | | disj2 4024 |
. . . . . . . . . . . . . . . . . 18
            
                           |
| 72 | | disjsn 4246 |
. . . . . . . . . . . . . . . . . 18
            
          
           |
| 73 | 71, 72 | bitr3i 266 |
. . . . . . . . . . . . . . . . 17
                    
              |
| 74 | 70, 73 | syl6bb 276 |
. . . . . . . . . . . . . . . 16
                         
               |
| 75 | 74 | elrab 3363 |
. . . . . . . . . . . . . . 15
                    
           
            
               |
| 76 | 58, 67, 75 | sylanbrc 698 |
. . . . . . . . . . . . . 14
    
    ..^ ..^                                   |
| 77 | | eqid 2622 |
. . . . . . . . . . . . . 14
      ..^ ..^               ..^ ..^         |
| 78 | 76, 77 | fmptd 6385 |
. . . . . . . . . . . . 13
         ..^ ..^            ..^ ..^               
            |
| 79 | 36 | oveq2d 6666 |
. . . . . . . . . . . . . . . . 17
                    |
| 80 | 49, 79 | eleqtrrd 2704 |
. . . . . . . . . . . . . . . 16
                |
| 81 | | swrd0val 13421 |
. . . . . . . . . . . . . . . 16
     Word Word    
             substr substr
         
  ..^ ..^    |
| 82 | 24, 80, 81 | syl2anc 693 |
. . . . . . . . . . . . . . 15
      substr substr          
  ..^ ..^    |
| 83 | 34 | feqmptd 6249 |
. . . . . . . . . . . . . . . 16
           ..^ ..^              |
| 84 | 83 | reseq1d 5395 |
. . . . . . . . . . . . . . 15
         ..^ ..^          ..^ ..^                ..^ ..^    |
| 85 | | resmpt 5449 |
. . . . . . . . . . . . . . . 16
    ..^ ..^     ..^ ..^             ..^ ..^                ..^ ..^         ..^ ..^          |
| 86 | 52, 53, 85 | 3syl 18 |
. . . . . . . . . . . . . . 15
          ..^ ..^             
  ..^ ..^         ..^ ..^          |
| 87 | 82, 84, 86 | 3eqtrd 2660 |
. . . . . . . . . . . . . 14
      substr substr             ..^ ..^          |
| 88 | 87 | feq1d 6030 |
. . . . . . . . . . . . 13
       substr substr          ..^ ..^                                 ..^ ..^            ..^ ..^               
             |
| 89 | 78, 88 | mpbird 247 |
. . . . . . . . . . . 12
      substr substr          ..^ ..^                            |
| 90 | 89 | adantr 481 |
. . . . . . . . . . 11
    
           substr substr          ..^ ..^               
            |
| 91 | | iswrdi 13309 |
. . . . . . . . . . 11
    substr substr          ..^ ..^               
              substr substr        Word Word             
            |
| 92 | 90, 91 | syl 17 |
. . . . . . . . . 10
    
           substr substr        Word Word             
            |
| 93 | | gsumwsubmcl 17375 |
. . . . . . . . . 10
                 
           SubMnd SubMnd      substr substr        Word Word             
                g g   substr substr                     
            |
| 94 | 47, 92, 93 | syl2anc 693 |
. . . . . . . . 9
    
            g g   substr substr                       
          |
| 95 | | difeq1 3721 |
. . . . . . . . . . . . . 14
       g g   substr substr        
   
      g g   substr substr            |
| 96 | 95 | dmeqd 5326 |
. . . . . . . . . . . . 13
       g g   substr substr        
            g g   substr
substr            |
| 97 | 96 | sseq1d 3632 |
. . . . . . . . . . . 12
       g g   substr substr        
               
     g g   substr substr          
          |
| 98 | 97 | elrab 3363 |
. . . . . . . . . . 11
     g g   substr substr                       
         
    g g   substr substr              
     g g   substr substr          
          |
| 99 | 98 | simprbi 480 |
. . . . . . . . . 10
     g g   substr substr                       
               g g   substr substr                    |
| 100 | | disj2 4024 |
. . . . . . . . . . 11
        g g   substr
substr          
             g g   substr substr                    |
| 101 | | disjsn 4246 |
. . . . . . . . . . 11
        g g   substr
substr          
          
     g g   substr substr            |
| 102 | 100, 101 | bitr3i 266 |
. . . . . . . . . 10
       g g   substr substr                   
        g g   substr
substr            |
| 103 | 99, 102 | sylib 208 |
. . . . . . . . 9
     g g   substr substr                       
            
     g g   substr substr            |
| 104 | 94, 103 | syl 17 |
. . . . . . . 8
    
           
     g g   substr substr            |
| 105 | | psgnunilem2.a |
. . . . . . . . 9
             
   |
| 106 | 105 | adantr 481 |
. . . . . . . 8
    
                      |
| 107 | 104, 106 | jca 554 |
. . . . . . 7
    
           
      g g   substr substr            
             |
| 108 | 107 | olcd 408 |
. . . . . 6
    
                  g g   substr substr                             
      g g   substr substr            
              |
| 109 | | excxor 1469 |
. . . . . 6
          g g   substr substr          
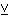              
   
     g g   substr substr          
                  
      g g   substr substr            
              |
| 110 | 108, 109 | sylibr 224 |
. . . . 5
    
           
     g g   substr substr          
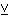               |
| 111 | | f1omvdco3 17869 |
. . . . 5
      g g   substr substr                               g g   substr substr          
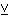                 
      g g   substr substr                   |
| 112 | 32, 43, 110, 111 | syl3anc 1326 |
. . . 4
    
                 g g   substr substr                   |
| 113 | 24 | adantr 481 |
. . . . . . . . . 10
    
           Word Word   |
| 114 | | elfzo0 12508 |
. . . . . . . . . . . . . . 15
      ..^ ..^       
         |
| 115 | 114 | simp2bi 1077 |
. . . . . . . . . . . . . 14
      ..^ ..^  
    |
| 116 | 35, 115 | syl 17 |
. . . . . . . . . . . . 13
        |
| 117 | 36, 116 | eqeltrd 2701 |
. . . . . . . . . . . 12
            |
| 118 | | wrdfin 13323 |
. . . . . . . . . . . . 13
    Word Word       |
| 119 | | hashnncl 13157 |
. . . . . . . . . . . . 13
              
     |
| 120 | 24, 118, 119 | 3syl 18 |
. . . . . . . . . . . 12
            
     |
| 121 | 117, 120 | mpbid 222 |
. . . . . . . . . . 11
        |
| 122 | 121 | adantr 481 |
. . . . . . . . . 10
    
             |
| 123 | | swrdccatwrd 13468 |
. . . . . . . . . . 11
     Word Word           substr substr
              ++ ++
   lastS lastS       
  |
| 124 | 123 | eqcomd 2628 |
. . . . . . . . . 10
     Word Word             substr substr               ++ ++    lastS lastS        |
| 125 | 113, 122,
124 | syl2anc 693 |
. . . . . . . . 9
    
              substr substr               ++ ++    lastS lastS        |
| 126 | 36 | oveq1d 6665 |
. . . . . . . . . . . 12
                    |
| 127 | 126 | adantr 481 |
. . . . . . . . . . 11
    
                         |
| 128 | 116 | nncnd 11036 |
. . . . . . . . . . . . 13
        |
| 129 | | 1cnd 10056 |
. . . . . . . . . . . . 13
        |
| 130 | | elfzoelz 12470 |
. . . . . . . . . . . . . . 15
      ..^ ..^  
    |
| 131 | 35, 130 | syl 17 |
. . . . . . . . . . . . . 14
        |
| 132 | 131 | zcnd 11483 |
. . . . . . . . . . . . 13
        |
| 133 | 128, 129,
132 | subadd2d 10411 |
. . . . . . . . . . . 12
                      |
| 134 | 133 | biimpar 502 |
. . . . . . . . . . 11
    
           
     |
| 135 | 127, 134 | eqtrd 2656 |
. . . . . . . . . 10
    
                     |
| 136 | | opeq2 4403 |
. . . . . . . . . . . . 13
                          
   
   |
| 137 | 136 | oveq2d 6666 |
. . . . . . . . . . . 12
                substr substr              
   substr substr        |
| 138 | 137 | adantl 482 |
. . . . . . . . . . 11
    
            
  substr substr                  substr substr        |
| 139 | | lsw 13351 |
. . . . . . . . . . . . . 14
    Word Word    lastS lastS                   |
| 140 | 24, 139 | syl 17 |
. . . . . . . . . . . . 13
     lastS lastS                   |
| 141 | | fveq2 6191 |
. . . . . . . . . . . . 13
                                  |
| 142 | 140, 141 | sylan9eq 2676 |
. . . . . . . . . . . 12
    
            
 lastS lastS           |
| 143 | 142 | s1eqd 13381 |
. . . . . . . . . . 11
    
            
   lastS lastS                 |
| 144 | 138, 143 | oveq12d 6668 |
. . . . . . . . . 10
    
            
   substr substr               ++ ++
   lastS lastS       
   substr substr       ++ ++            |
| 145 | 135, 144 | syldan 487 |
. . . . . . . . 9
    
            substr substr
              ++ ++
   lastS lastS       
   substr substr       ++ ++            |
| 146 | 125, 145 | eqtrd 2656 |
. . . . . . . 8
    
              substr substr       ++ ++            |
| 147 | 146 | oveq2d 6666 |
. . . . . . 7
    
            g g       g g    substr substr       ++ ++             |
| 148 | 40 | s1cld 13383 |
. . . . . . . . 9
              Word Word
      |
| 149 | | eqid 2622 |
. . . . . . . . . 10
            |
| 150 | 20, 149 | gsumccat 17378 |
. . . . . . . . 9
         substr
substr        Word Word                 Word Word           g g    substr substr       ++ ++                 g g   substr substr                g g             |
| 151 | 18, 27, 148, 150 | syl3anc 1326 |
. . . . . . . 8
       g g    substr substr       ++ ++                 g g   substr substr                g g             |
| 152 | 151 | adantr 481 |
. . . . . . 7
    
            g g    substr substr       ++ ++                 g g   substr substr                g g             |
| 153 | 20 | gsumws1 17376 |
. . . . . . . . . . 11
             
   g g           
      |
| 154 | 40, 153 | syl 17 |
. . . . . . . . . 10
       g g           
      |
| 155 | 154 | oveq2d 6666 |
. . . . . . . . 9
        g g   substr substr                g g                 g g   substr substr                    |
| 156 | 15, 20, 149 | symgov 17810 |
. . . . . . . . . 10
      g g   substr substr              
            
    g g   substr substr                        g g   substr substr                |
| 157 | 29, 40, 156 | syl2anc 693 |
. . . . . . . . 9
        g g   substr substr                        g g   substr substr                |
| 158 | 155, 157 | eqtrd 2656 |
. . . . . . . 8
        g g   substr substr                g g                 g g   substr substr                |
| 159 | 158 | adantr 481 |
. . . . . . 7
    
             g g   substr substr                g g                 g g   substr substr                |
| 160 | 147, 152,
159 | 3eqtrd 2660 |
. . . . . 6
    
            g g        g g   substr substr                |
| 161 | 160 | difeq1d 3727 |
. . . . 5
    
             g g      
     g g   substr substr                   |
| 162 | 161 | dmeqd 5326 |
. . . 4
    
              g g             g g   substr substr                   |
| 163 | 112, 162 | eleqtrrd 2704 |
. . 3
    
                g g       |
| 164 | 13, 163 | mtand 691 |
. 2
             |
| 165 | | fzostep1 12584 |
. . . 4
      ..^ ..^  
         ..^ ..^            |
| 166 | 35, 165 | syl 17 |
. . 3
             ..^ ..^            |
| 167 | 166 | ord 392 |
. 2
              ..^ ..^            |
| 168 | 164, 167 | mt3d 140 |
1
            ..^ ..^   |