Theorem prlem934 9855

Description: Lemma 9-3.4 of [Gleason] p. 122. (Contributed by NM, 25-Mar-1996.) (Revised by Mario Carneiro, 11-May-2013.) (New usage is discouraged.)

Hypothesis

Ref	Expression
prlem934.1	|- B e. _V

Assertion

Ref	Expression
prlem934	|- ( A e. P. -> E. x e. A -. ( x +Q B ) e. A )

Distinct variable groups:   x, A   x, B

Proof of Theorem prlem934

Dummy variables b w y z v are mutually distinct and distinct from all other variables.

Step	Hyp	Ref	Expression
1		prn0 9811	. . . . 5 |- ( A e. P. -> A =/= (/) )
2		r19.2z 4060	. . . . . 6 |- ( ( A =/= (/) /\ A. x e. A ( x +Q B ) e. A ) -> E. x e. A ( x +Q B ) e. A )
3	2	ex 450	. . . . 5 |- ( A =/= (/) -> ( A. x e. A ( x +Q B ) e. A -> E. x e. A ( x +Q B ) e. A ) )
4	1, 3	syl 17	. . . 4 |- ( A e. P. -> ( A. x e. A ( x +Q B ) e. A -> E. x e. A ( x +Q B ) e. A ) )
5		prpssnq 9812	. . . . . . . . 9 |- ( A e. P. -> A C. Q. )
6	5	pssssd 3704	. . . . . . . 8 |- ( A e. P. -> A C_ Q. )
7	6	sseld 3602	. . . . . . 7 |- ( A e. P. -> ( ( x +Q B ) e. A -> ( x +Q B ) e. Q. ) )
8		addnqf 9770	. . . . . . . . . 10 |- +Q : ( Q. X. Q. ) --> Q.
9	8	fdmi 6052	. . . . . . . . 9 |- dom +Q = ( Q. X. Q. )
10		0nnq 9746	. . . . . . . . 9 |- -. (/) e. Q.
11	9, 10	ndmovrcl 6820	. . . . . . . 8 |- ( ( x +Q B ) e. Q. -> ( x e. Q. /\ B e. Q. ) )
12	11	simprd 479	. . . . . . 7 |- ( ( x +Q B ) e. Q. -> B e. Q. )
13	7, 12	syl6com 37	. . . . . 6 |- ( ( x +Q B ) e. A -> ( A e. P. -> B e. Q. ) )
14	13	rexlimivw 3029	. . . . 5 |- ( E. x e. A ( x +Q B ) e. A -> ( A e. P. -> B e. Q. ) )
15	14	com12 32	. . . 4 |- ( A e. P. -> ( E. x e. A ( x +Q B ) e. A -> B e. Q. ) )
16		oveq2 6658	. . . . . . . . . 10 |- ( b = B -> ( x +Q b ) = ( x +Q B ) )
17	16	eleq1d 2686	. . . . . . . . 9 |- ( b = B -> ( ( x +Q b ) e. A <-> ( x +Q B ) e. A ) )
18	17	ralbidv 2986	. . . . . . . 8 |- ( b = B -> ( A. x e. A ( x +Q b ) e. A <-> A. x e. A ( x +Q B ) e. A ) )
19	18	notbid 308	. . . . . . 7 |- ( b = B -> ( -. A. x e. A ( x +Q b ) e. A <-> -. A. x e. A ( x +Q B ) e. A ) )
20	19	imbi2d 330	. . . . . 6 |- ( b = B -> ( ( A e. P. -> -. A. x e. A ( x +Q b ) e. A ) <-> ( A e. P. -> -. A. x e. A ( x +Q B ) e. A ) ) )
21		dfpss2 3692	. . . . . . . . . . 11 |- ( A C. Q. <-> ( A C_ Q. /\ -. A = Q. ) )
22	5, 21	sylib 208	. . . . . . . . . 10 |- ( A e. P. -> ( A C_ Q. /\ -. A = Q. ) )
23	22	simprd 479	. . . . . . . . 9 |- ( A e. P. -> -. A = Q. )
24	23	adantr 481	. . . . . . . 8 |- ( ( A e. P. /\ b e. Q. ) -> -. A = Q. )
25	6	3ad2ant1 1082	. . . . . . . . . 10 |- ( ( A e. P. /\ b e. Q. /\ A. x e. A ( x +Q b ) e. A ) -> A C_ Q. )
26		simpl1 1064	. . . . . . . . . . . . . 14 |- ( ( ( A e. P. /\ b e. Q. /\ A. x e. A ( x +Q b ) e. A ) /\ w e. Q. ) -> A e. P. )
27		n0 3931	. . . . . . . . . . . . . . 15 |- ( A =/= (/) <-> E. y y e. A )
28	1, 27	sylib 208	. . . . . . . . . . . . . 14 |- ( A e. P. -> E. y y e. A )
29	26, 28	syl 17	. . . . . . . . . . . . 13 |- ( ( ( A e. P. /\ b e. Q. /\ A. x e. A ( x +Q b ) e. A ) /\ w e. Q. ) -> E. y y e. A )
30		simprl 794	. . . . . . . . . . . . . . . . 17 |- ( ( ( A e. P. /\ b e. Q. /\ A. x e. A ( x +Q b ) e. A ) /\ ( w e. Q. /\ y e. A ) ) -> w e. Q. )
31		simpl2 1065	. . . . . . . . . . . . . . . . 17 |- ( ( ( A e. P. /\ b e. Q. /\ A. x e. A ( x +Q b ) e. A ) /\ ( w e. Q. /\ y e. A ) ) -> b e. Q. )
32		recclnq 9788	. . . . . . . . . . . . . . . . . 18 |- ( b e. Q. -> ( *Q ` b ) e. Q. )
33		mulclnq 9769	. . . . . . . . . . . . . . . . . . 19 |- ( ( w e. Q. /\ ( *Q ` b ) e. Q. ) -> ( w .Q ( *Q ` b ) ) e. Q. )
34		archnq 9802	. . . . . . . . . . . . . . . . . . 19 |- ( ( w .Q ( *Q ` b ) ) e. Q. -> E. z e. N. ( w .Q ( *Q ` b ) ) <Q <. z , 1o >. )
35	33, 34	syl 17	. . . . . . . . . . . . . . . . . 18 |- ( ( w e. Q. /\ ( *Q ` b ) e. Q. ) -> E. z e. N. ( w .Q ( *Q ` b ) ) <Q <. z , 1o >. )
36	32, 35	sylan2 491	. . . . . . . . . . . . . . . . 17 |- ( ( w e. Q. /\ b e. Q. ) -> E. z e. N. ( w .Q ( *Q ` b ) ) <Q <. z , 1o >. )
37	30, 31, 36	syl2anc 693	. . . . . . . . . . . . . . . 16 |- ( ( ( A e. P. /\ b e. Q. /\ A. x e. A ( x +Q b ) e. A ) /\ ( w e. Q. /\ y e. A ) ) -> E. z e. N. ( w .Q ( *Q ` b ) ) <Q <. z , 1o >. )
38		simpll2 1101	. . . . . . . . . . . . . . . . . . 19 |- ( ( ( ( A e. P. /\ b e. Q. /\ A. x e. A ( x +Q b ) e. A ) /\ ( w e. Q. /\ y e. A ) ) /\ ( z e. N. /\ ( w .Q ( *Q ` b ) ) <Q <. z , 1o >. ) ) -> b e. Q. )
39		simplrl 800	. . . . . . . . . . . . . . . . . . 19 |- ( ( ( ( A e. P. /\ b e. Q. /\ A. x e. A ( x +Q b ) e. A ) /\ ( w e. Q. /\ y e. A ) ) /\ ( z e. N. /\ ( w .Q ( *Q ` b ) ) <Q <. z , 1o >. ) ) -> w e. Q. )
40		simprr 796	. . . . . . . . . . . . . . . . . . 19 |- ( ( ( ( A e. P. /\ b e. Q. /\ A. x e. A ( x +Q b ) e. A ) /\ ( w e. Q. /\ y e. A ) ) /\ ( z e. N. /\ ( w .Q ( *Q ` b ) ) <Q <. z , 1o >. ) ) -> ( w .Q ( *Q ` b ) ) <Q <. z , 1o >. )
41		ltmnq 9794	. . . . . . . . . . . . . . . . . . . . . . 23 |- ( b e. Q. -> ( ( w .Q ( *Q ` b ) ) <Q <. z , 1o >. <-> ( b .Q ( w .Q ( *Q ` b ) ) ) <Q ( b .Q <. z , 1o >. ) ) )
42		vex 3203	. . . . . . . . . . . . . . . . . . . . . . . . 25 |- b e. _V
43		vex 3203	. . . . . . . . . . . . . . . . . . . . . . . . 25 |- w e. _V
44		fvex 6201	. . . . . . . . . . . . . . . . . . . . . . . . 25 |- ( *Q ` b ) e. _V
45		mulcomnq 9775	. . . . . . . . . . . . . . . . . . . . . . . . 25 |- ( v .Q x ) = ( x .Q v )
46		mulassnq 9781	. . . . . . . . . . . . . . . . . . . . . . . . 25 |- ( ( v .Q x ) .Q y ) = ( v .Q ( x .Q y ) )
47	42, 43, 44, 45, 46	caov12 6862	. . . . . . . . . . . . . . . . . . . . . . . 24 |- ( b .Q ( w .Q ( *Q ` b ) ) ) = ( w .Q ( b .Q ( *Q ` b ) ) )
48		mulcomnq 9775	. . . . . . . . . . . . . . . . . . . . . . . 24 |- ( b .Q <. z , 1o >. ) = ( <. z , 1o >. .Q b )
49	47, 48	breq12i 4662	. . . . . . . . . . . . . . . . . . . . . . 23 |- ( ( b .Q ( w .Q ( *Q ` b ) ) ) <Q ( b .Q <. z , 1o >. ) <-> ( w .Q ( b .Q ( *Q ` b ) ) ) <Q ( <. z , 1o >. .Q b ) )
50	41, 49	syl6bb 276	. . . . . . . . . . . . . . . . . . . . . 22 |- ( b e. Q. -> ( ( w .Q ( *Q ` b ) ) <Q <. z , 1o >. <-> ( w .Q ( b .Q ( *Q ` b ) ) ) <Q ( <. z , 1o >. .Q b ) ) )
51	50	adantr 481	. . . . . . . . . . . . . . . . . . . . 21 |- ( ( b e. Q. /\ w e. Q. ) -> ( ( w .Q ( *Q ` b ) ) <Q <. z , 1o >. <-> ( w .Q ( b .Q ( *Q ` b ) ) ) <Q ( <. z , 1o >. .Q b ) ) )
52		recidnq 9787	. . . . . . . . . . . . . . . . . . . . . . . 24 |- ( b e. Q. -> ( b .Q ( *Q ` b ) ) = 1Q )
53	52	oveq2d 6666	. . . . . . . . . . . . . . . . . . . . . . 23 |- ( b e. Q. -> ( w .Q ( b .Q ( *Q ` b ) ) ) = ( w .Q 1Q ) )
54		mulidnq 9785	. . . . . . . . . . . . . . . . . . . . . . 23 |- ( w e. Q. -> ( w .Q 1Q ) = w )
55	53, 54	sylan9eq 2676	. . . . . . . . . . . . . . . . . . . . . 22 |- ( ( b e. Q. /\ w e. Q. ) -> ( w .Q ( b .Q ( *Q ` b ) ) ) = w )
56	55	breq1d 4663	. . . . . . . . . . . . . . . . . . . . 21 |- ( ( b e. Q. /\ w e. Q. ) -> ( ( w .Q ( b .Q ( *Q ` b ) ) ) <Q ( <. z , 1o >. .Q b ) <-> w <Q ( <. z , 1o >. .Q b ) ) )
57	51, 56	bitrd 268	. . . . . . . . . . . . . . . . . . . 20 |- ( ( b e. Q. /\ w e. Q. ) -> ( ( w .Q ( *Q ` b ) ) <Q <. z , 1o >. <-> w <Q ( <. z , 1o >. .Q b ) ) )
58	57	biimpa 501	. . . . . . . . . . . . . . . . . . 19 |- ( ( ( b e. Q. /\ w e. Q. ) /\ ( w .Q ( *Q ` b ) ) <Q <. z , 1o >. ) -> w <Q ( <. z , 1o >. .Q b ) )
59	38, 39, 40, 58	syl21anc 1325	. . . . . . . . . . . . . . . . . 18 |- ( ( ( ( A e. P. /\ b e. Q. /\ A. x e. A ( x +Q b ) e. A ) /\ ( w e. Q. /\ y e. A ) ) /\ ( z e. N. /\ ( w .Q ( *Q ` b ) ) <Q <. z , 1o >. ) ) -> w <Q ( <. z , 1o >. .Q b ) )
60		simprl 794	. . . . . . . . . . . . . . . . . . . 20 |- ( ( ( ( A e. P. /\ b e. Q. /\ A. x e. A ( x +Q b ) e. A ) /\ ( w e. Q. /\ y e. A ) ) /\ ( z e. N. /\ ( w .Q ( *Q ` b ) ) <Q <. z , 1o >. ) ) -> z e. N. )
61		pinq 9749	. . . . . . . . . . . . . . . . . . . . 21 |- ( z e. N. -> <. z , 1o >. e. Q. )
62		mulclnq 9769	. . . . . . . . . . . . . . . . . . . . 21 |- ( ( <. z , 1o >. e. Q. /\ b e. Q. ) -> ( <. z , 1o >. .Q b ) e. Q. )
63	61, 62	sylan 488	. . . . . . . . . . . . . . . . . . . 20 |- ( ( z e. N. /\ b e. Q. ) -> ( <. z , 1o >. .Q b ) e. Q. )
64	60, 38, 63	syl2anc 693	. . . . . . . . . . . . . . . . . . 19 |- ( ( ( ( A e. P. /\ b e. Q. /\ A. x e. A ( x +Q b ) e. A ) /\ ( w e. Q. /\ y e. A ) ) /\ ( z e. N. /\ ( w .Q ( *Q ` b ) ) <Q <. z , 1o >. ) ) -> ( <. z , 1o >. .Q b ) e. Q. )
65		simpll1 1100	. . . . . . . . . . . . . . . . . . . 20 |- ( ( ( ( A e. P. /\ b e. Q. /\ A. x e. A ( x +Q b ) e. A ) /\ ( w e. Q. /\ y e. A ) ) /\ ( z e. N. /\ ( w .Q ( *Q ` b ) ) <Q <. z , 1o >. ) ) -> A e. P. )
66		simplrr 801	. . . . . . . . . . . . . . . . . . . 20 |- ( ( ( ( A e. P. /\ b e. Q. /\ A. x e. A ( x +Q b ) e. A ) /\ ( w e. Q. /\ y e. A ) ) /\ ( z e. N. /\ ( w .Q ( *Q ` b ) ) <Q <. z , 1o >. ) ) -> y e. A )
67		elprnq 9813	. . . . . . . . . . . . . . . . . . . 20 |- ( ( A e. P. /\ y e. A ) -> y e. Q. )
68	65, 66, 67	syl2anc 693	. . . . . . . . . . . . . . . . . . 19 |- ( ( ( ( A e. P. /\ b e. Q. /\ A. x e. A ( x +Q b ) e. A ) /\ ( w e. Q. /\ y e. A ) ) /\ ( z e. N. /\ ( w .Q ( *Q ` b ) ) <Q <. z , 1o >. ) ) -> y e. Q. )
69		ltaddnq 9796	. . . . . . . . . . . . . . . . . . . 20 |- ( ( ( <. z , 1o >. .Q b ) e. Q. /\ y e. Q. ) -> ( <. z , 1o >. .Q b ) <Q ( ( <. z , 1o >. .Q b ) +Q y ) )
70		addcomnq 9773	. . . . . . . . . . . . . . . . . . . 20 |- ( ( <. z , 1o >. .Q b ) +Q y ) = ( y +Q ( <. z , 1o >. .Q b ) )
71	69, 70	syl6breq 4694	. . . . . . . . . . . . . . . . . . 19 |- ( ( ( <. z , 1o >. .Q b ) e. Q. /\ y e. Q. ) -> ( <. z , 1o >. .Q b ) <Q ( y +Q ( <. z , 1o >. .Q b ) ) )
72	64, 68, 71	syl2anc 693	. . . . . . . . . . . . . . . . . 18 |- ( ( ( ( A e. P. /\ b e. Q. /\ A. x e. A ( x +Q b ) e. A ) /\ ( w e. Q. /\ y e. A ) ) /\ ( z e. N. /\ ( w .Q ( *Q ` b ) ) <Q <. z , 1o >. ) ) -> ( <. z , 1o >. .Q b ) <Q ( y +Q ( <. z , 1o >. .Q b ) ) )
73		ltsonq 9791	. . . . . . . . . . . . . . . . . . 19 |- <Q Or Q.
74		ltrelnq 9748	. . . . . . . . . . . . . . . . . . 19 |- <Q C_ ( Q. X. Q. )
75	73, 74	sotri 5523	. . . . . . . . . . . . . . . . . 18 |- ( ( w <Q ( <. z , 1o >. .Q b ) /\ ( <. z , 1o >. .Q b ) <Q ( y +Q ( <. z , 1o >. .Q b ) ) ) -> w <Q ( y +Q ( <. z , 1o >. .Q b ) ) )
76	59, 72, 75	syl2anc 693	. . . . . . . . . . . . . . . . 17 |- ( ( ( ( A e. P. /\ b e. Q. /\ A. x e. A ( x +Q b ) e. A ) /\ ( w e. Q. /\ y e. A ) ) /\ ( z e. N. /\ ( w .Q ( *Q ` b ) ) <Q <. z , 1o >. ) ) -> w <Q ( y +Q ( <. z , 1o >. .Q b ) ) )
77		simpll3 1102	. . . . . . . . . . . . . . . . . . 19 |- ( ( ( ( A e. P. /\ b e. Q. /\ A. x e. A ( x +Q b ) e. A ) /\ ( w e. Q. /\ y e. A ) ) /\ ( z e. N. /\ ( w .Q ( *Q ` b ) ) <Q <. z , 1o >. ) ) -> A. x e. A ( x +Q b ) e. A )
78		opeq1 4402	. . . . . . . . . . . . . . . . . . . . . . . . . 26 |- ( w = 1o -> <. w , 1o >. = <. 1o , 1o >. )
79		df-1nq 9738	. . . . . . . . . . . . . . . . . . . . . . . . . 26 |- 1Q = <. 1o , 1o >.
80	78, 79	syl6eqr 2674	. . . . . . . . . . . . . . . . . . . . . . . . 25 |- ( w = 1o -> <. w , 1o >. = 1Q )
81	80	oveq1d 6665	. . . . . . . . . . . . . . . . . . . . . . . 24 |- ( w = 1o -> ( <. w , 1o >. .Q b ) = ( 1Q .Q b ) )
82	81	oveq2d 6666	. . . . . . . . . . . . . . . . . . . . . . 23 |- ( w = 1o -> ( y +Q ( <. w , 1o >. .Q b ) ) = ( y +Q ( 1Q .Q b ) ) )
83	82	eleq1d 2686	. . . . . . . . . . . . . . . . . . . . . 22 |- ( w = 1o -> ( ( y +Q ( <. w , 1o >. .Q b ) ) e. A <-> ( y +Q ( 1Q .Q b ) ) e. A ) )
84	83	imbi2d 330	. . . . . . . . . . . . . . . . . . . . 21 |- ( w = 1o -> ( ( ( b e. Q. /\ A. x e. A ( x +Q b ) e. A /\ y e. A ) -> ( y +Q ( <. w , 1o >. .Q b ) ) e. A ) <-> ( ( b e. Q. /\ A. x e. A ( x +Q b ) e. A /\ y e. A ) -> ( y +Q ( 1Q .Q b ) ) e. A ) ) )
85		opeq1 4402	. . . . . . . . . . . . . . . . . . . . . . . . 25 |- ( w = z -> <. w , 1o >. = <. z , 1o >. )
86	85	oveq1d 6665	. . . . . . . . . . . . . . . . . . . . . . . 24 |- ( w = z -> ( <. w , 1o >. .Q b ) = ( <. z , 1o >. .Q b ) )
87	86	oveq2d 6666	. . . . . . . . . . . . . . . . . . . . . . 23 |- ( w = z -> ( y +Q ( <. w , 1o >. .Q b ) ) = ( y +Q ( <. z , 1o >. .Q b ) ) )
88	87	eleq1d 2686	. . . . . . . . . . . . . . . . . . . . . 22 |- ( w = z -> ( ( y +Q ( <. w , 1o >. .Q b ) ) e. A <-> ( y +Q ( <. z , 1o >. .Q b ) ) e. A ) )
89	88	imbi2d 330	. . . . . . . . . . . . . . . . . . . . 21 |- ( w = z -> ( ( ( b e. Q. /\ A. x e. A ( x +Q b ) e. A /\ y e. A ) -> ( y +Q ( <. w , 1o >. .Q b ) ) e. A ) <-> ( ( b e. Q. /\ A. x e. A ( x +Q b ) e. A /\ y e. A ) -> ( y +Q ( <. z , 1o >. .Q b ) ) e. A ) ) )
90		opeq1 4402	. . . . . . . . . . . . . . . . . . . . . . . . 25 |- ( w = ( z +N 1o ) -> <. w , 1o >. = <. ( z +N 1o ) , 1o >. )
91	90	oveq1d 6665	. . . . . . . . . . . . . . . . . . . . . . . 24 |- ( w = ( z +N 1o ) -> ( <. w , 1o >. .Q b ) = ( <. ( z +N 1o ) , 1o >. .Q b ) )
92	91	oveq2d 6666	. . . . . . . . . . . . . . . . . . . . . . 23 |- ( w = ( z +N 1o ) -> ( y +Q ( <. w , 1o >. .Q b ) ) = ( y +Q ( <. ( z +N 1o ) , 1o >. .Q b ) ) )
93	92	eleq1d 2686	. . . . . . . . . . . . . . . . . . . . . 22 |- ( w = ( z +N 1o ) -> ( ( y +Q ( <. w , 1o >. .Q b ) ) e. A <-> ( y +Q ( <. ( z +N 1o ) , 1o >. .Q b ) ) e. A ) )
94	93	imbi2d 330	. . . . . . . . . . . . . . . . . . . . 21 |- ( w = ( z +N 1o ) -> ( ( ( b e. Q. /\ A. x e. A ( x +Q b ) e. A /\ y e. A ) -> ( y +Q ( <. w , 1o >. .Q b ) ) e. A ) <-> ( ( b e. Q. /\ A. x e. A ( x +Q b ) e. A /\ y e. A ) -> ( y +Q ( <. ( z +N 1o ) , 1o >. .Q b ) ) e. A ) ) )
95		mulcomnq 9775	. . . . . . . . . . . . . . . . . . . . . . . 24 |- ( 1Q .Q b ) = ( b .Q 1Q )
96		mulidnq 9785	. . . . . . . . . . . . . . . . . . . . . . . 24 |- ( b e. Q. -> ( b .Q 1Q ) = b )
97	95, 96	syl5eq 2668	. . . . . . . . . . . . . . . . . . . . . . 23 |- ( b e. Q. -> ( 1Q .Q b ) = b )
98		oveq1 6657	. . . . . . . . . . . . . . . . . . . . . . . . 25 |- ( x = y -> ( x +Q b ) = ( y +Q b ) )
99	98	eleq1d 2686	. . . . . . . . . . . . . . . . . . . . . . . 24 |- ( x = y -> ( ( x +Q b ) e. A <-> ( y +Q b ) e. A ) )
100	99	rspccva 3308	. . . . . . . . . . . . . . . . . . . . . . 23 |- ( ( A. x e. A ( x +Q b ) e. A /\ y e. A ) -> ( y +Q b ) e. A )
101		oveq2 6658	. . . . . . . . . . . . . . . . . . . . . . . . 25 |- ( ( 1Q .Q b ) = b -> ( y +Q ( 1Q .Q b ) ) = ( y +Q b ) )
102	101	eleq1d 2686	. . . . . . . . . . . . . . . . . . . . . . . 24 |- ( ( 1Q .Q b ) = b -> ( ( y +Q ( 1Q .Q b ) ) e. A <-> ( y +Q b ) e. A ) )
103	102	biimpar 502	. . . . . . . . . . . . . . . . . . . . . . 23 |- ( ( ( 1Q .Q b ) = b /\ ( y +Q b ) e. A ) -> ( y +Q ( 1Q .Q b ) ) e. A )
104	97, 100, 103	syl2an 494	. . . . . . . . . . . . . . . . . . . . . 22 |- ( ( b e. Q. /\ ( A. x e. A ( x +Q b ) e. A /\ y e. A ) ) -> ( y +Q ( 1Q .Q b ) ) e. A )
105	104	3impb 1260	. . . . . . . . . . . . . . . . . . . . 21 |- ( ( b e. Q. /\ A. x e. A ( x +Q b ) e. A /\ y e. A ) -> ( y +Q ( 1Q .Q b ) ) e. A )
106		3simpa 1058	. . . . . . . . . . . . . . . . . . . . . . 23 |- ( ( b e. Q. /\ A. x e. A ( x +Q b ) e. A /\ y e. A ) -> ( b e. Q. /\ A. x e. A ( x +Q b ) e. A ) )
107		oveq1 6657	. . . . . . . . . . . . . . . . . . . . . . . . . . . 28 |- ( x = ( y +Q ( <. z , 1o >. .Q b ) ) -> ( x +Q b ) = ( ( y +Q ( <. z , 1o >. .Q b ) ) +Q b ) )
108	107	eleq1d 2686	. . . . . . . . . . . . . . . . . . . . . . . . . . 27 |- ( x = ( y +Q ( <. z , 1o >. .Q b ) ) -> ( ( x +Q b ) e. A <-> ( ( y +Q ( <. z , 1o >. .Q b ) ) +Q b ) e. A ) )
109	108	rspccva 3308	. . . . . . . . . . . . . . . . . . . . . . . . . 26 |- ( ( A. x e. A ( x +Q b ) e. A /\ ( y +Q ( <. z , 1o >. .Q b ) ) e. A ) -> ( ( y +Q ( <. z , 1o >. .Q b ) ) +Q b ) e. A )
110		addassnq 9780	. . . . . . . . . . . . . . . . . . . . . . . . . . . 28 |- ( ( y +Q ( <. z , 1o >. .Q b ) ) +Q b ) = ( y +Q ( ( <. z , 1o >. .Q b ) +Q b ) )
111		opex 4932	. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 32 |- <. z , 1o >. e. _V
112		1nq 9750	. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 33 |- 1Q e. Q.
113	112	elexi 3213	. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 32 |- 1Q e. _V
114		distrnq 9783	. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 32 |- ( v .Q ( x +Q y ) ) = ( ( v .Q x ) +Q ( v .Q y ) )
115	111, 113, 42, 45, 114	caovdir 6868	. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 31 |- ( ( <. z , 1o >. +Q 1Q ) .Q b ) = ( ( <. z , 1o >. .Q b ) +Q ( 1Q .Q b ) )
116	115	a1i 11	. . . . . . . . . . . . . . . . . . . . . . . . . . . . . 30 |- ( ( z e. N. /\ b e. Q. ) -> ( ( <. z , 1o >. +Q 1Q ) .Q b ) = ( ( <. z , 1o >. .Q b ) +Q ( 1Q .Q b ) ) )
117		addpqnq 9760	. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 34 |- ( ( <. z , 1o >. e. Q. /\ 1Q e. Q. ) -> ( <. z , 1o >. +Q 1Q ) = ( /Q ` ( <. z , 1o >. +pQ 1Q ) ) )
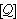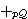118	61, 112, 117	sylancl 694	. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 33 |- ( z e. N. -> ( <. z , 1o >. +Q 1Q ) = ( /Q ` ( <. z , 1o >. +pQ 1Q ) ) )
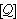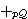119	79	oveq2i 6661	. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 36 |- ( <. z , 1o >. +pQ 1Q ) = ( <. z , 1o >. +pQ <. 1o , 1o >. )
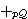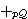120		1pi 9705	. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 37 |- 1o e. N.
121		addpipq 9759	. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 38 |- ( ( ( z e. N. /\ 1o e. N. ) /\ ( 1o e. N. /\ 1o e. N. ) ) -> ( <. z , 1o >. +pQ <. 1o , 1o >. ) = <. ( ( z .N 1o ) +N ( 1o .N 1o ) ) , ( 1o .N 1o ) >. )
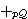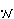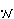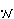122	120, 120, 121	mpanr12 721	. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 37 |- ( ( z e. N. /\ 1o e. N. ) -> ( <. z , 1o >. +pQ <. 1o , 1o >. ) = <. ( ( z .N 1o ) +N ( 1o .N 1o ) ) , ( 1o .N 1o ) >. )
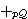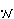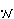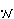123	120, 122	mpan2 707	. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 36 |- ( z e. N. -> ( <. z , 1o >. +pQ <. 1o , 1o >. ) = <. ( ( z .N 1o ) +N ( 1o .N 1o ) ) , ( 1o .N 1o ) >. )
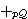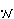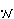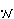124	119, 123	syl5eq 2668	. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 35 |- ( z e. N. -> ( <. z , 1o >. +pQ 1Q ) = <. ( ( z .N 1o ) +N ( 1o .N 1o ) ) , ( 1o .N 1o ) >. )
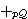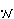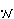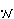125		mulidpi 9708	. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 37 |- ( z e. N. -> ( z .N 1o ) = z )
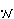126		mulidpi 9708	. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 38 |- ( 1o e. N. -> ( 1o .N 1o ) = 1o )
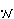127	120, 126	mp1i 13	. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 37 |- ( z e. N. -> ( 1o .N 1o ) = 1o )
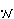128	125, 127	oveq12d 6668	. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 36 |- ( z e. N. -> ( ( z .N 1o ) +N ( 1o .N 1o ) ) = ( z +N 1o ) )
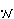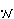129	128, 127	opeq12d 4410	. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 35 |- ( z e. N. -> <. ( ( z .N 1o ) +N ( 1o .N 1o ) ) , ( 1o .N 1o ) >. = <. ( z +N 1o ) , 1o >. )
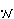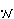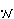
130	124, 129	eqtrd 2656	. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 34 |- ( z e. N. -> ( <. z , 1o >. +pQ 1Q ) = <. ( z +N 1o ) , 1o >. )
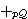131	130	fveq2d 6195	. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 33 |- ( z e. N. -> ( /Q ` ( <. z , 1o >. +pQ 1Q ) ) = ( /Q ` <. ( z +N 1o ) , 1o >. ) )
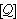
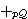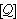132		addclpi 9714	. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 35 |- ( ( z e. N. /\ 1o e. N. ) -> ( z +N 1o ) e. N. )
133	120, 132	mpan2 707	. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 34 |- ( z e. N. -> ( z +N 1o ) e. N. )
134		pinq 9749	. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 34 |- ( ( z +N 1o ) e. N. -> <. ( z +N 1o ) , 1o >. e. Q. )
135		nqerid 9755	. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 34 |- ( <. ( z +N 1o ) , 1o >. e. Q. -> ( /Q ` <. ( z +N 1o ) , 1o >. ) = <. ( z +N 1o ) , 1o >. )
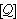136	133, 134, 135	3syl 18	. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 33 |- ( z e. N. -> ( /Q ` <. ( z +N 1o ) , 1o >. ) = <. ( z +N 1o ) , 1o >. )
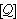137	118, 131, 136	3eqtrd 2660	. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 32 |- ( z e. N. -> ( <. z , 1o >. +Q 1Q ) = <. ( z +N 1o ) , 1o >. )
138	137	adantr 481	. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 31 |- ( ( z e. N. /\ b e. Q. ) -> ( <. z , 1o >. +Q 1Q ) = <. ( z +N 1o ) , 1o >. )
139	138	oveq1d 6665	. . . . . . . . . . . . . . . . . . . . . . . . . . . . . 30 |- ( ( z e. N. /\ b e. Q. ) -> ( ( <. z , 1o >. +Q 1Q ) .Q b ) = ( <. ( z +N 1o ) , 1o >. .Q b ) )
140	97	adantl 482	. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 31 |- ( ( z e. N. /\ b e. Q. ) -> ( 1Q .Q b ) = b )
141	140	oveq2d 6666	. . . . . . . . . . . . . . . . . . . . . . . . . . . . . 30 |- ( ( z e. N. /\ b e. Q. ) -> ( ( <. z , 1o >. .Q b ) +Q ( 1Q .Q b ) ) = ( ( <. z , 1o >. .Q b ) +Q b ) )
142	116, 139, 141	3eqtr3rd 2665	. . . . . . . . . . . . . . . . . . . . . . . . . . . . 29 |- ( ( z e. N. /\ b e. Q. ) -> ( ( <. z , 1o >. .Q b ) +Q b ) = ( <. ( z +N 1o ) , 1o >. .Q b ) )
143	142	oveq2d 6666	. . . . . . . . . . . . . . . . . . . . . . . . . . . 28 |- ( ( z e. N. /\ b e. Q. ) -> ( y +Q ( ( <. z , 1o >. .Q b ) +Q b ) ) = ( y +Q ( <. ( z +N 1o ) , 1o >. .Q b ) ) )
144	110, 143	syl5eq 2668	. . . . . . . . . . . . . . . . . . . . . . . . . . 27 |- ( ( z e. N. /\ b e. Q. ) -> ( ( y +Q ( <. z , 1o >. .Q b ) ) +Q b ) = ( y +Q ( <. ( z +N 1o ) , 1o >. .Q b ) ) )
145	144	eleq1d 2686	. . . . . . . . . . . . . . . . . . . . . . . . . 26 |- ( ( z e. N. /\ b e. Q. ) -> ( ( ( y +Q ( <. z , 1o >. .Q b ) ) +Q b ) e. A <-> ( y +Q ( <. ( z +N 1o ) , 1o >. .Q b ) ) e. A ) )
146	109, 145	syl5ib 234	. . . . . . . . . . . . . . . . . . . . . . . . 25 |- ( ( z e. N. /\ b e. Q. ) -> ( ( A. x e. A ( x +Q b ) e. A /\ ( y +Q ( <. z , 1o >. .Q b ) ) e. A ) -> ( y +Q ( <. ( z +N 1o ) , 1o >. .Q b ) ) e. A ) )
147	146	expd 452	. . . . . . . . . . . . . . . . . . . . . . . 24 |- ( ( z e. N. /\ b e. Q. ) -> ( A. x e. A ( x +Q b ) e. A -> ( ( y +Q ( <. z , 1o >. .Q b ) ) e. A -> ( y +Q ( <. ( z +N 1o ) , 1o >. .Q b ) ) e. A ) ) )
148	147	expimpd 629	. . . . . . . . . . . . . . . . . . . . . . 23 |- ( z e. N. -> ( ( b e. Q. /\ A. x e. A ( x +Q b ) e. A ) -> ( ( y +Q ( <. z , 1o >. .Q b ) ) e. A -> ( y +Q ( <. ( z +N 1o ) , 1o >. .Q b ) ) e. A ) ) )
149	106, 148	syl5 34	. . . . . . . . . . . . . . . . . . . . . 22 |- ( z e. N. -> ( ( b e. Q. /\ A. x e. A ( x +Q b ) e. A /\ y e. A ) -> ( ( y +Q ( <. z , 1o >. .Q b ) ) e. A -> ( y +Q ( <. ( z +N 1o ) , 1o >. .Q b ) ) e. A ) ) )
150	149	a2d 29	. . . . . . . . . . . . . . . . . . . . 21 |- ( z e. N. -> ( ( ( b e. Q. /\ A. x e. A ( x +Q b ) e. A /\ y e. A ) -> ( y +Q ( <. z , 1o >. .Q b ) ) e. A ) -> ( ( b e. Q. /\ A. x e. A ( x +Q b ) e. A /\ y e. A ) -> ( y +Q ( <. ( z +N 1o ) , 1o >. .Q b ) ) e. A ) ) )
151	84, 89, 94, 89, 105, 150	indpi 9729	. . . . . . . . . . . . . . . . . . . 20 |- ( z e. N. -> ( ( b e. Q. /\ A. x e. A ( x +Q b ) e. A /\ y e. A ) -> ( y +Q ( <. z , 1o >. .Q b ) ) e. A ) )
152	151	imp 445	. . . . . . . . . . . . . . . . . . 19 |- ( ( z e. N. /\ ( b e. Q. /\ A. x e. A ( x +Q b ) e. A /\ y e. A ) ) -> ( y +Q ( <. z , 1o >. .Q b ) ) e. A )
153	60, 38, 77, 66, 152	syl13anc 1328	. . . . . . . . . . . . . . . . . 18 |- ( ( ( ( A e. P. /\ b e. Q. /\ A. x e. A ( x +Q b ) e. A ) /\ ( w e. Q. /\ y e. A ) ) /\ ( z e. N. /\ ( w .Q ( *Q ` b ) ) <Q <. z , 1o >. ) ) -> ( y +Q ( <. z , 1o >. .Q b ) ) e. A )
154		prcdnq 9815	. . . . . . . . . . . . . . . . . 18 |- ( ( A e. P. /\ ( y +Q ( <. z , 1o >. .Q b ) ) e. A ) -> ( w <Q ( y +Q ( <. z , 1o >. .Q b ) ) -> w e. A ) )
155	65, 153, 154	syl2anc 693	. . . . . . . . . . . . . . . . 17 |- ( ( ( ( A e. P. /\ b e. Q. /\ A. x e. A ( x +Q b ) e. A ) /\ ( w e. Q. /\ y e. A ) ) /\ ( z e. N. /\ ( w .Q ( *Q ` b ) ) <Q <. z , 1o >. ) ) -> ( w <Q ( y +Q ( <. z , 1o >. .Q b ) ) -> w e. A ) )
156	76, 155	mpd 15	. . . . . . . . . . . . . . . 16 |- ( ( ( ( A e. P. /\ b e. Q. /\ A. x e. A ( x +Q b ) e. A ) /\ ( w e. Q. /\ y e. A ) ) /\ ( z e. N. /\ ( w .Q ( *Q ` b ) ) <Q <. z , 1o >. ) ) -> w e. A )
157	37, 156	rexlimddv 3035	. . . . . . . . . . . . . . 15 |- ( ( ( A e. P. /\ b e. Q. /\ A. x e. A ( x +Q b ) e. A ) /\ ( w e. Q. /\ y e. A ) ) -> w e. A )
158	157	expr 643	. . . . . . . . . . . . . 14 |- ( ( ( A e. P. /\ b e. Q. /\ A. x e. A ( x +Q b ) e. A ) /\ w e. Q. ) -> ( y e. A -> w e. A ) )
159	158	exlimdv 1861	. . . . . . . . . . . . 13 |- ( ( ( A e. P. /\ b e. Q. /\ A. x e. A ( x +Q b ) e. A ) /\ w e. Q. ) -> ( E. y y e. A -> w e. A ) )
160	29, 159	mpd 15	. . . . . . . . . . . 12 |- ( ( ( A e. P. /\ b e. Q. /\ A. x e. A ( x +Q b ) e. A ) /\ w e. Q. ) -> w e. A )
161	160	ex 450	. . . . . . . . . . 11 |- ( ( A e. P. /\ b e. Q. /\ A. x e. A ( x +Q b ) e. A ) -> ( w e. Q. -> w e. A ) )
162	161	ssrdv 3609	. . . . . . . . . 10 |- ( ( A e. P. /\ b e. Q. /\ A. x e. A ( x +Q b ) e. A ) -> Q. C_ A )
163	25, 162	eqssd 3620	. . . . . . . . 9 |- ( ( A e. P. /\ b e. Q. /\ A. x e. A ( x +Q b ) e. A ) -> A = Q. )
164	163	3expia 1267	. . . . . . . 8 |- ( ( A e. P. /\ b e. Q. ) -> ( A. x e. A ( x +Q b ) e. A -> A = Q. ) )
165	24, 164	mtod 189	. . . . . . 7 |- ( ( A e. P. /\ b e. Q. ) -> -. A. x e. A ( x +Q b ) e. A )
166	165	expcom 451	. . . . . 6 |- ( b e. Q. -> ( A e. P. -> -. A. x e. A ( x +Q b ) e. A ) )
167	20, 166	vtoclga 3272	. . . . 5 |- ( B e. Q. -> ( A e. P. -> -. A. x e. A ( x +Q B ) e. A ) )
168	167	com12 32	. . . 4 |- ( A e. P. -> ( B e. Q. -> -. A. x e. A ( x +Q B ) e. A ) )
169	4, 15, 168	3syld 60	. . 3 |- ( A e. P. -> ( A. x e. A ( x +Q B ) e. A -> -. A. x e. A ( x +Q B ) e. A ) )
170	169	pm2.01d 181	. 2 |- ( A e. P. -> -. A. x e. A ( x +Q B ) e. A )
171		rexnal 2995	. 2 |- ( E. x e. A -. ( x +Q B ) e. A <-> -. A. x e. A ( x +Q B ) e. A )
172	170, 171	sylibr 224	1 |- ( A e. P. -> E. x e. A -. ( x +Q B ) e. A )

Syntax hints:   -. wn 3   -> wi 4   <-> wb 196   /\ wa 384   /\ w3a 1037   = wceq 1483   E.wex 1704   e. wcel 1990   =/= wne 2794   A.wral 2912   E.wrex 2913   _Vcvv 3200   C_ wss 3574   C. wpss 3575   (/)c0 3915   <.cop 4183   class class class wbr 4653   X. cxp 5112   ` cfv 5888  (class class class)co 6650   1oc1o 7553   N.cnpi 9666   +N cpli 9667   .N cmi 9668   +pQ cplpq 9670   Q.cnq 9674   1Qc1q 9675   /Qcerq 9676   +Q cplq 9677   .Q cmq 9678   *Qcrq 9679   <Q cltq 9680   P.cnp 9681

This theorem was proved from axioms:  ax-mp 5  ax-1 6  ax-2 7  ax-3 8  ax-gen 1722  ax-4 1737  ax-5 1839  ax-6 1888  ax-7 1935  ax-8 1992  ax-9 1999  ax-10 2019  ax-11 2034  ax-12 2047  ax-13 2246  ax-ext 2602  ax-sep 4781  ax-nul 4789  ax-pow 4843  ax-pr 4906  ax-un 6949

This theorem depends on definitions:  df-bi 197  df-or 385  df-an 386  df-3or 1038  df-3an 1039  df-tru 1486  df-ex 1705  df-nf 1710  df-sb 1881  df-eu 2474  df-mo 2475  df-clab 2609  df-cleq 2615  df-clel 2618  df-nfc 2753  df-ne 2795  df-ral 2917  df-rex 2918  df-reu 2919  df-rmo 2920  df-rab 2921  df-v 3202  df-sbc 3436  df-csb 3534  df-dif 3577  df-un 3579  df-in 3581  df-ss 3588  df-pss 3590  df-nul 3916  df-if 4087  df-pw 4160  df-sn 4178  df-pr 4180  df-tp 4182  df-op 4184  df-uni 4437  df-int 4476  df-iun 4522  df-br 4654  df-opab 4713  df-mpt 4730  df-tr 4753  df-id 5024  df-eprel 5029  df-po 5035  df-so 5036  df-fr 5073  df-we 5075  df-xp 5120  df-rel 5121  df-cnv 5122  df-co 5123  df-dm 5124  df-rn 5125  df-res 5126  df-ima 5127  df-pred 5680  df-ord 5726  df-on 5727  df-lim 5728  df-suc 5729  df-iota 5851  df-fun 5890  df-fn 5891  df-f 5892  df-f1 5893  df-fo 5894  df-f1o 5895  df-fv 5896  df-ov 6653  df-oprab 6654  df-mpt2 6655  df-om 7066  df-1st 7168  df-2nd 7169  df-wrecs 7407  df-recs 7468  df-rdg 7506  df-1o 7560  df-oadd 7564  df-omul 7565  df-er 7742  df-ni 9694  df-pli 9695  df-mi 9696  df-lti 9697  df-plpq 9730  df-mpq 9731  df-ltpq 9732  df-enq 9733  df-nq 9734  df-erq 9735  df-plq 9736  df-mq 9737  df-1nq 9738  df-rq 9739  df-ltnq 9740  df-np 9803

This theorem is referenced by:  ltaddpr  9856  ltexprlem7  9864  prlem936  9869