Theorem ipidsq 27565

Description: The inner product of a vector with itself is the square of the vector's norm. Equation I4 of [Ponnusamy] p. 362. (Contributed by NM, 1-Feb-2007.) (New usage is discouraged.)

Hypotheses

Ref	Expression
ipid.1	|- X = ( BaseSet ` U )
ipid.6	|- N = ( normCV ` U )
ipid.7	|- P = ( .iOLD ` U )

Assertion

Ref	Expression
ipidsq	|- ( ( U e. NrmCVec /\ A e. X ) -> ( A P A ) = ( ( N ` A ) ^ 2 ) )

Proof of Theorem ipidsq

Step	Hyp	Ref	Expression
1		ipid.1	. . . 4 |- X = ( BaseSet ` U )
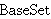2		eqid 2622	. . . 4 |- ( +v ` U ) = ( +v ` U )
3		eqid 2622	. . . 4 |- ( .sOLD ` U ) = ( .sOLD ` U )
4		ipid.6	. . . 4 |- N = ( normCV ` U )
5		ipid.7	. . . 4 |- P = ( .iOLD ` U )
6	1, 2, 3, 4, 5	ipval2 27562	. . 3 |- ( ( U e. NrmCVec /\ A e. X /\ A e. X ) -> ( A P A ) = ( ( ( ( ( N ` ( A ( +v ` U ) A ) ) ^ 2 ) - ( ( N ` ( A ( +v ` U ) ( -u 1 ( .sOLD ` U ) A ) ) ) ^ 2 ) ) + ( _i x. ( ( ( N ` ( A ( +v ` U ) ( _i ( .sOLD ` U ) A ) ) ) ^ 2 ) - ( ( N ` ( A ( +v ` U ) ( -u _i ( .sOLD ` U ) A ) ) ) ^ 2 ) ) ) ) / 4 ) )
7	6	3anidm23 1385	. 2 |- ( ( U e. NrmCVec /\ A e. X ) -> ( A P A ) = ( ( ( ( ( N ` ( A ( +v ` U ) A ) ) ^ 2 ) - ( ( N ` ( A ( +v ` U ) ( -u 1 ( .sOLD ` U ) A ) ) ) ^ 2 ) ) + ( _i x. ( ( ( N ` ( A ( +v ` U ) ( _i ( .sOLD ` U ) A ) ) ) ^ 2 ) - ( ( N ` ( A ( +v ` U ) ( -u _i ( .sOLD ` U ) A ) ) ) ^ 2 ) ) ) ) / 4 ) )
8	1, 2, 3	nv2 27487	. . . . . . . . . . 11 |- ( ( U e. NrmCVec /\ A e. X ) -> ( A ( +v ` U ) A ) = ( 2 ( .sOLD ` U ) A ) )
9	8	fveq2d 6195	. . . . . . . . . 10 |- ( ( U e. NrmCVec /\ A e. X ) -> ( N ` ( A ( +v ` U ) A ) ) = ( N ` ( 2 ( .sOLD ` U ) A ) ) )
10		2re 11090	. . . . . . . . . . . 12 |- 2 e. RR
11		0le2 11111	. . . . . . . . . . . 12 |- 0 <_ 2
12	10, 11	pm3.2i 471	. . . . . . . . . . 11 |- ( 2 e. RR /\ 0 <_ 2 )
13	1, 3, 4	nvsge0 27519	. . . . . . . . . . 11 |- ( ( U e. NrmCVec /\ ( 2 e. RR /\ 0 <_ 2 ) /\ A e. X ) -> ( N ` ( 2 ( .sOLD ` U ) A ) ) = ( 2 x. ( N ` A ) ) )
14	12, 13	mp3an2 1412	. . . . . . . . . 10 |- ( ( U e. NrmCVec /\ A e. X ) -> ( N ` ( 2 ( .sOLD ` U ) A ) ) = ( 2 x. ( N ` A ) ) )
15	9, 14	eqtrd 2656	. . . . . . . . 9 |- ( ( U e. NrmCVec /\ A e. X ) -> ( N ` ( A ( +v ` U ) A ) ) = ( 2 x. ( N ` A ) ) )
16	15	oveq1d 6665	. . . . . . . 8 |- ( ( U e. NrmCVec /\ A e. X ) -> ( ( N ` ( A ( +v ` U ) A ) ) ^ 2 ) = ( ( 2 x. ( N ` A ) ) ^ 2 ) )
17	1, 4	nvcl 27516	. . . . . . . . . . 11 |- ( ( U e. NrmCVec /\ A e. X ) -> ( N ` A ) e. RR )
18	17	recnd 10068	. . . . . . . . . 10 |- ( ( U e. NrmCVec /\ A e. X ) -> ( N ` A ) e. CC )
19		2cn 11091	. . . . . . . . . . 11 |- 2 e. CC
20		2nn0 11309	. . . . . . . . . . 11 |- 2 e. NN0
21		mulexp 12899	. . . . . . . . . . 11 |- ( ( 2 e. CC /\ ( N ` A ) e. CC /\ 2 e. NN0 ) -> ( ( 2 x. ( N ` A ) ) ^ 2 ) = ( ( 2 ^ 2 ) x. ( ( N ` A ) ^ 2 ) ) )
22	19, 20, 21	mp3an13 1415	. . . . . . . . . 10 |- ( ( N ` A ) e. CC -> ( ( 2 x. ( N ` A ) ) ^ 2 ) = ( ( 2 ^ 2 ) x. ( ( N ` A ) ^ 2 ) ) )
23	18, 22	syl 17	. . . . . . . . 9 |- ( ( U e. NrmCVec /\ A e. X ) -> ( ( 2 x. ( N ` A ) ) ^ 2 ) = ( ( 2 ^ 2 ) x. ( ( N ` A ) ^ 2 ) ) )
24		sq2 12960	. . . . . . . . . 10 |- ( 2 ^ 2 ) = 4
25	24	oveq1i 6660	. . . . . . . . 9 |- ( ( 2 ^ 2 ) x. ( ( N ` A ) ^ 2 ) ) = ( 4 x. ( ( N ` A ) ^ 2 ) )
26	23, 25	syl6eq 2672	. . . . . . . 8 |- ( ( U e. NrmCVec /\ A e. X ) -> ( ( 2 x. ( N ` A ) ) ^ 2 ) = ( 4 x. ( ( N ` A ) ^ 2 ) ) )
27	16, 26	eqtrd 2656	. . . . . . 7 |- ( ( U e. NrmCVec /\ A e. X ) -> ( ( N ` ( A ( +v ` U ) A ) ) ^ 2 ) = ( 4 x. ( ( N ` A ) ^ 2 ) ) )
28		eqid 2622	. . . . . . . . . . 11 |- ( 0vec ` U ) = ( 0vec ` U )
29	1, 2, 3, 28	nvrinv 27506	. . . . . . . . . 10 |- ( ( U e. NrmCVec /\ A e. X ) -> ( A ( +v ` U ) ( -u 1 ( .sOLD ` U ) A ) ) = ( 0vec ` U ) )
30	29	fveq2d 6195	. . . . . . . . 9 |- ( ( U e. NrmCVec /\ A e. X ) -> ( N ` ( A ( +v ` U ) ( -u 1 ( .sOLD ` U ) A ) ) ) = ( N ` ( 0vec ` U ) ) )
31	28, 4	nvz0 27523	. . . . . . . . . 10 |- ( U e. NrmCVec -> ( N ` ( 0vec ` U ) ) = 0 )
32	31	adantr 481	. . . . . . . . 9 |- ( ( U e. NrmCVec /\ A e. X ) -> ( N ` ( 0vec ` U ) ) = 0 )
33	30, 32	eqtrd 2656	. . . . . . . 8 |- ( ( U e. NrmCVec /\ A e. X ) -> ( N ` ( A ( +v ` U ) ( -u 1 ( .sOLD ` U ) A ) ) ) = 0 )
34	33	sq0id 12957	. . . . . . 7 |- ( ( U e. NrmCVec /\ A e. X ) -> ( ( N ` ( A ( +v ` U ) ( -u 1 ( .sOLD ` U ) A ) ) ) ^ 2 ) = 0 )
35	27, 34	oveq12d 6668	. . . . . 6 |- ( ( U e. NrmCVec /\ A e. X ) -> ( ( ( N ` ( A ( +v ` U ) A ) ) ^ 2 ) - ( ( N ` ( A ( +v ` U ) ( -u 1 ( .sOLD ` U ) A ) ) ) ^ 2 ) ) = ( ( 4 x. ( ( N ` A ) ^ 2 ) ) - 0 ) )
36		4cn 11098	. . . . . . . 8 |- 4 e. CC
37	18	sqcld 13006	. . . . . . . 8 |- ( ( U e. NrmCVec /\ A e. X ) -> ( ( N ` A ) ^ 2 ) e. CC )
38		mulcl 10020	. . . . . . . 8 |- ( ( 4 e. CC /\ ( ( N ` A ) ^ 2 ) e. CC ) -> ( 4 x. ( ( N ` A ) ^ 2 ) ) e. CC )
39	36, 37, 38	sylancr 695	. . . . . . 7 |- ( ( U e. NrmCVec /\ A e. X ) -> ( 4 x. ( ( N ` A ) ^ 2 ) ) e. CC )
40	39	subid1d 10381	. . . . . 6 |- ( ( U e. NrmCVec /\ A e. X ) -> ( ( 4 x. ( ( N ` A ) ^ 2 ) ) - 0 ) = ( 4 x. ( ( N ` A ) ^ 2 ) ) )
41	35, 40	eqtrd 2656	. . . . 5 |- ( ( U e. NrmCVec /\ A e. X ) -> ( ( ( N ` ( A ( +v ` U ) A ) ) ^ 2 ) - ( ( N ` ( A ( +v ` U ) ( -u 1 ( .sOLD ` U ) A ) ) ) ^ 2 ) ) = ( 4 x. ( ( N ` A ) ^ 2 ) ) )
42		1re 10039	. . . . . . . . . . . . . . . 16 |- 1 e. RR
43		neg1rr 11125	. . . . . . . . . . . . . . . 16 |- -u 1 e. RR
44		absreim 14033	. . . . . . . . . . . . . . . 16 |- ( ( 1 e. RR /\ -u 1 e. RR ) -> ( abs ` ( 1 + ( _i x. -u 1 ) ) ) = ( sqr ` ( ( 1 ^ 2 ) + ( -u 1 ^ 2 ) ) ) )
45	42, 43, 44	mp2an 708	. . . . . . . . . . . . . . 15 |- ( abs ` ( 1 + ( _i x. -u 1 ) ) ) = ( sqr ` ( ( 1 ^ 2 ) + ( -u 1 ^ 2 ) ) )
46		ax-icn 9995	. . . . . . . . . . . . . . . . . . 19 |- _i e. CC
47		ax-1cn 9994	. . . . . . . . . . . . . . . . . . 19 |- 1 e. CC
48	46, 47	mulneg2i 10477	. . . . . . . . . . . . . . . . . 18 |- ( _i x. -u 1 ) = -u ( _i x. 1 )
49	46	mulid1i 10042	. . . . . . . . . . . . . . . . . . 19 |- ( _i x. 1 ) = _i
50	49	negeqi 10274	. . . . . . . . . . . . . . . . . 18 |- -u ( _i x. 1 ) = -u _i
51	48, 50	eqtri 2644	. . . . . . . . . . . . . . . . 17 |- ( _i x. -u 1 ) = -u _i
52	51	oveq2i 6661	. . . . . . . . . . . . . . . 16 |- ( 1 + ( _i x. -u 1 ) ) = ( 1 + -u _i )
53	52	fveq2i 6194	. . . . . . . . . . . . . . 15 |- ( abs ` ( 1 + ( _i x. -u 1 ) ) ) = ( abs ` ( 1 + -u _i ) )
54		sqneg 12923	. . . . . . . . . . . . . . . . . 18 |- ( 1 e. CC -> ( -u 1 ^ 2 ) = ( 1 ^ 2 ) )
55	47, 54	ax-mp 5	. . . . . . . . . . . . . . . . 17 |- ( -u 1 ^ 2 ) = ( 1 ^ 2 )
56	55	oveq2i 6661	. . . . . . . . . . . . . . . 16 |- ( ( 1 ^ 2 ) + ( -u 1 ^ 2 ) ) = ( ( 1 ^ 2 ) + ( 1 ^ 2 ) )
57	56	fveq2i 6194	. . . . . . . . . . . . . . 15 |- ( sqr ` ( ( 1 ^ 2 ) + ( -u 1 ^ 2 ) ) ) = ( sqr ` ( ( 1 ^ 2 ) + ( 1 ^ 2 ) ) )
58	45, 53, 57	3eqtr3i 2652	. . . . . . . . . . . . . 14 |- ( abs ` ( 1 + -u _i ) ) = ( sqr ` ( ( 1 ^ 2 ) + ( 1 ^ 2 ) ) )
59		absreim 14033	. . . . . . . . . . . . . . 15 |- ( ( 1 e. RR /\ 1 e. RR ) -> ( abs ` ( 1 + ( _i x. 1 ) ) ) = ( sqr ` ( ( 1 ^ 2 ) + ( 1 ^ 2 ) ) ) )
60	42, 42, 59	mp2an 708	. . . . . . . . . . . . . 14 |- ( abs ` ( 1 + ( _i x. 1 ) ) ) = ( sqr ` ( ( 1 ^ 2 ) + ( 1 ^ 2 ) ) )
61	49	oveq2i 6661	. . . . . . . . . . . . . . 15 |- ( 1 + ( _i x. 1 ) ) = ( 1 + _i )
62	61	fveq2i 6194	. . . . . . . . . . . . . 14 |- ( abs ` ( 1 + ( _i x. 1 ) ) ) = ( abs ` ( 1 + _i ) )
63	58, 60, 62	3eqtr2i 2650	. . . . . . . . . . . . 13 |- ( abs ` ( 1 + -u _i ) ) = ( abs ` ( 1 + _i ) )
64	63	oveq1i 6660	. . . . . . . . . . . 12 |- ( ( abs ` ( 1 + -u _i ) ) x. ( N ` A ) ) = ( ( abs ` ( 1 + _i ) ) x. ( N ` A ) )
65		negicn 10282	. . . . . . . . . . . . . 14 |- -u _i e. CC
66	47, 65	addcli 10044	. . . . . . . . . . . . 13 |- ( 1 + -u _i ) e. CC
67	1, 3, 4	nvs 27518	. . . . . . . . . . . . 13 |- ( ( U e. NrmCVec /\ ( 1 + -u _i ) e. CC /\ A e. X ) -> ( N ` ( ( 1 + -u _i ) ( .sOLD ` U ) A ) ) = ( ( abs ` ( 1 + -u _i ) ) x. ( N ` A ) ) )
68	66, 67	mp3an2 1412	. . . . . . . . . . . 12 |- ( ( U e. NrmCVec /\ A e. X ) -> ( N ` ( ( 1 + -u _i ) ( .sOLD ` U ) A ) ) = ( ( abs ` ( 1 + -u _i ) ) x. ( N ` A ) ) )
69	47, 46	addcli 10044	. . . . . . . . . . . . 13 |- ( 1 + _i ) e. CC
70	1, 3, 4	nvs 27518	. . . . . . . . . . . . 13 |- ( ( U e. NrmCVec /\ ( 1 + _i ) e. CC /\ A e. X ) -> ( N ` ( ( 1 + _i ) ( .sOLD ` U ) A ) ) = ( ( abs ` ( 1 + _i ) ) x. ( N ` A ) ) )
71	69, 70	mp3an2 1412	. . . . . . . . . . . 12 |- ( ( U e. NrmCVec /\ A e. X ) -> ( N ` ( ( 1 + _i ) ( .sOLD ` U ) A ) ) = ( ( abs ` ( 1 + _i ) ) x. ( N ` A ) ) )
72	64, 68, 71	3eqtr4a 2682	. . . . . . . . . . 11 |- ( ( U e. NrmCVec /\ A e. X ) -> ( N ` ( ( 1 + -u _i ) ( .sOLD ` U ) A ) ) = ( N ` ( ( 1 + _i ) ( .sOLD ` U ) A ) ) )
73	1, 2, 3	nvdir 27486	. . . . . . . . . . . . . . 15 |- ( ( U e. NrmCVec /\ ( 1 e. CC /\ -u _i e. CC /\ A e. X ) ) -> ( ( 1 + -u _i ) ( .sOLD ` U ) A ) = ( ( 1 ( .sOLD ` U ) A ) ( +v ` U ) ( -u _i ( .sOLD ` U ) A ) ) )
74	47, 73	mp3anr1 1421	. . . . . . . . . . . . . 14 |- ( ( U e. NrmCVec /\ ( -u _i e. CC /\ A e. X ) ) -> ( ( 1 + -u _i ) ( .sOLD ` U ) A ) = ( ( 1 ( .sOLD ` U ) A ) ( +v ` U ) ( -u _i ( .sOLD ` U ) A ) ) )
75	65, 74	mpanr1 719	. . . . . . . . . . . . 13 |- ( ( U e. NrmCVec /\ A e. X ) -> ( ( 1 + -u _i ) ( .sOLD ` U ) A ) = ( ( 1 ( .sOLD ` U ) A ) ( +v ` U ) ( -u _i ( .sOLD ` U ) A ) ) )
76	1, 3	nvsid 27482	. . . . . . . . . . . . . 14 |- ( ( U e. NrmCVec /\ A e. X ) -> ( 1 ( .sOLD ` U ) A ) = A )
77	76	oveq1d 6665	. . . . . . . . . . . . 13 |- ( ( U e. NrmCVec /\ A e. X ) -> ( ( 1 ( .sOLD ` U ) A ) ( +v ` U ) ( -u _i ( .sOLD ` U ) A ) ) = ( A ( +v ` U ) ( -u _i ( .sOLD ` U ) A ) ) )
78	75, 77	eqtrd 2656	. . . . . . . . . . . 12 |- ( ( U e. NrmCVec /\ A e. X ) -> ( ( 1 + -u _i ) ( .sOLD ` U ) A ) = ( A ( +v ` U ) ( -u _i ( .sOLD ` U ) A ) ) )
79	78	fveq2d 6195	. . . . . . . . . . 11 |- ( ( U e. NrmCVec /\ A e. X ) -> ( N ` ( ( 1 + -u _i ) ( .sOLD ` U ) A ) ) = ( N ` ( A ( +v ` U ) ( -u _i ( .sOLD ` U ) A ) ) ) )
80	1, 2, 3	nvdir 27486	. . . . . . . . . . . . . . 15 |- ( ( U e. NrmCVec /\ ( 1 e. CC /\ _i e. CC /\ A e. X ) ) -> ( ( 1 + _i ) ( .sOLD ` U ) A ) = ( ( 1 ( .sOLD ` U ) A ) ( +v ` U ) ( _i ( .sOLD ` U ) A ) ) )
81	47, 80	mp3anr1 1421	. . . . . . . . . . . . . 14 |- ( ( U e. NrmCVec /\ ( _i e. CC /\ A e. X ) ) -> ( ( 1 + _i ) ( .sOLD ` U ) A ) = ( ( 1 ( .sOLD ` U ) A ) ( +v ` U ) ( _i ( .sOLD ` U ) A ) ) )
82	46, 81	mpanr1 719	. . . . . . . . . . . . 13 |- ( ( U e. NrmCVec /\ A e. X ) -> ( ( 1 + _i ) ( .sOLD ` U ) A ) = ( ( 1 ( .sOLD ` U ) A ) ( +v ` U ) ( _i ( .sOLD ` U ) A ) ) )
83	76	oveq1d 6665	. . . . . . . . . . . . 13 |- ( ( U e. NrmCVec /\ A e. X ) -> ( ( 1 ( .sOLD ` U ) A ) ( +v ` U ) ( _i ( .sOLD ` U ) A ) ) = ( A ( +v ` U ) ( _i ( .sOLD ` U ) A ) ) )
84	82, 83	eqtrd 2656	. . . . . . . . . . . 12 |- ( ( U e. NrmCVec /\ A e. X ) -> ( ( 1 + _i ) ( .sOLD ` U ) A ) = ( A ( +v ` U ) ( _i ( .sOLD ` U ) A ) ) )
85	84	fveq2d 6195	. . . . . . . . . . 11 |- ( ( U e. NrmCVec /\ A e. X ) -> ( N ` ( ( 1 + _i ) ( .sOLD ` U ) A ) ) = ( N ` ( A ( +v ` U ) ( _i ( .sOLD ` U ) A ) ) ) )
86	72, 79, 85	3eqtr3d 2664	. . . . . . . . . 10 |- ( ( U e. NrmCVec /\ A e. X ) -> ( N ` ( A ( +v ` U ) ( -u _i ( .sOLD ` U ) A ) ) ) = ( N ` ( A ( +v ` U ) ( _i ( .sOLD ` U ) A ) ) ) )
87	86	oveq1d 6665	. . . . . . . . 9 |- ( ( U e. NrmCVec /\ A e. X ) -> ( ( N ` ( A ( +v ` U ) ( -u _i ( .sOLD ` U ) A ) ) ) ^ 2 ) = ( ( N ` ( A ( +v ` U ) ( _i ( .sOLD ` U ) A ) ) ) ^ 2 ) )
88	87	oveq2d 6666	. . . . . . . 8 |- ( ( U e. NrmCVec /\ A e. X ) -> ( ( ( N ` ( A ( +v ` U ) ( _i ( .sOLD ` U ) A ) ) ) ^ 2 ) - ( ( N ` ( A ( +v ` U ) ( -u _i ( .sOLD ` U ) A ) ) ) ^ 2 ) ) = ( ( ( N ` ( A ( +v ` U ) ( _i ( .sOLD ` U ) A ) ) ) ^ 2 ) - ( ( N ` ( A ( +v ` U ) ( _i ( .sOLD ` U ) A ) ) ) ^ 2 ) ) )
89	1, 2, 3, 4, 5	ipval2lem4 27561	. . . . . . . . . . 11 |- ( ( ( U e. NrmCVec /\ A e. X /\ A e. X ) /\ _i e. CC ) -> ( ( N ` ( A ( +v ` U ) ( _i ( .sOLD ` U ) A ) ) ) ^ 2 ) e. CC )
90	46, 89	mpan2 707	. . . . . . . . . 10 |- ( ( U e. NrmCVec /\ A e. X /\ A e. X ) -> ( ( N ` ( A ( +v ` U ) ( _i ( .sOLD ` U ) A ) ) ) ^ 2 ) e. CC )
91	90	3anidm23 1385	. . . . . . . . 9 |- ( ( U e. NrmCVec /\ A e. X ) -> ( ( N ` ( A ( +v ` U ) ( _i ( .sOLD ` U ) A ) ) ) ^ 2 ) e. CC )
92	91	subidd 10380	. . . . . . . 8 |- ( ( U e. NrmCVec /\ A e. X ) -> ( ( ( N ` ( A ( +v ` U ) ( _i ( .sOLD ` U ) A ) ) ) ^ 2 ) - ( ( N ` ( A ( +v ` U ) ( _i ( .sOLD ` U ) A ) ) ) ^ 2 ) ) = 0 )
93	88, 92	eqtrd 2656	. . . . . . 7 |- ( ( U e. NrmCVec /\ A e. X ) -> ( ( ( N ` ( A ( +v ` U ) ( _i ( .sOLD ` U ) A ) ) ) ^ 2 ) - ( ( N ` ( A ( +v ` U ) ( -u _i ( .sOLD ` U ) A ) ) ) ^ 2 ) ) = 0 )
94	93	oveq2d 6666	. . . . . 6 |- ( ( U e. NrmCVec /\ A e. X ) -> ( _i x. ( ( ( N ` ( A ( +v ` U ) ( _i ( .sOLD ` U ) A ) ) ) ^ 2 ) - ( ( N ` ( A ( +v ` U ) ( -u _i ( .sOLD ` U ) A ) ) ) ^ 2 ) ) ) = ( _i x. 0 ) )
95		it0e0 11254	. . . . . 6 |- ( _i x. 0 ) = 0
96	94, 95	syl6eq 2672	. . . . 5 |- ( ( U e. NrmCVec /\ A e. X ) -> ( _i x. ( ( ( N ` ( A ( +v ` U ) ( _i ( .sOLD ` U ) A ) ) ) ^ 2 ) - ( ( N ` ( A ( +v ` U ) ( -u _i ( .sOLD ` U ) A ) ) ) ^ 2 ) ) ) = 0 )
97	41, 96	oveq12d 6668	. . . 4 |- ( ( U e. NrmCVec /\ A e. X ) -> ( ( ( ( N ` ( A ( +v ` U ) A ) ) ^ 2 ) - ( ( N ` ( A ( +v ` U ) ( -u 1 ( .sOLD ` U ) A ) ) ) ^ 2 ) ) + ( _i x. ( ( ( N ` ( A ( +v ` U ) ( _i ( .sOLD ` U ) A ) ) ) ^ 2 ) - ( ( N ` ( A ( +v ` U ) ( -u _i ( .sOLD ` U ) A ) ) ) ^ 2 ) ) ) ) = ( ( 4 x. ( ( N ` A ) ^ 2 ) ) + 0 ) )
98	39	addid1d 10236	. . . 4 |- ( ( U e. NrmCVec /\ A e. X ) -> ( ( 4 x. ( ( N ` A ) ^ 2 ) ) + 0 ) = ( 4 x. ( ( N ` A ) ^ 2 ) ) )
99	97, 98	eqtr2d 2657	. . 3 |- ( ( U e. NrmCVec /\ A e. X ) -> ( 4 x. ( ( N ` A ) ^ 2 ) ) = ( ( ( ( N ` ( A ( +v ` U ) A ) ) ^ 2 ) - ( ( N ` ( A ( +v ` U ) ( -u 1 ( .sOLD ` U ) A ) ) ) ^ 2 ) ) + ( _i x. ( ( ( N ` ( A ( +v ` U ) ( _i ( .sOLD ` U ) A ) ) ) ^ 2 ) - ( ( N ` ( A ( +v ` U ) ( -u _i ( .sOLD ` U ) A ) ) ) ^ 2 ) ) ) ) )
100	99	oveq1d 6665	. 2 |- ( ( U e. NrmCVec /\ A e. X ) -> ( ( 4 x. ( ( N ` A ) ^ 2 ) ) / 4 ) = ( ( ( ( ( N ` ( A ( +v ` U ) A ) ) ^ 2 ) - ( ( N ` ( A ( +v ` U ) ( -u 1 ( .sOLD ` U ) A ) ) ) ^ 2 ) ) + ( _i x. ( ( ( N ` ( A ( +v ` U ) ( _i ( .sOLD ` U ) A ) ) ) ^ 2 ) - ( ( N ` ( A ( +v ` U ) ( -u _i ( .sOLD ` U ) A ) ) ) ^ 2 ) ) ) ) / 4 ) )
101		4ne0 11117	. . . 4 |- 4 =/= 0
102		divcan3 10711	. . . 4 |- ( ( ( ( N ` A ) ^ 2 ) e. CC /\ 4 e. CC /\ 4 =/= 0 ) -> ( ( 4 x. ( ( N ` A ) ^ 2 ) ) / 4 ) = ( ( N ` A ) ^ 2 ) )
103	36, 101, 102	mp3an23 1416	. . 3 |- ( ( ( N ` A ) ^ 2 ) e. CC -> ( ( 4 x. ( ( N ` A ) ^ 2 ) ) / 4 ) = ( ( N ` A ) ^ 2 ) )
104	37, 103	syl 17	. 2 |- ( ( U e. NrmCVec /\ A e. X ) -> ( ( 4 x. ( ( N ` A ) ^ 2 ) ) / 4 ) = ( ( N ` A ) ^ 2 ) )
105	7, 100, 104	3eqtr2d 2662	1 |- ( ( U e. NrmCVec /\ A e. X ) -> ( A P A ) = ( ( N ` A ) ^ 2 ) )

Syntax hints:   -> wi 4   /\ wa 384   /\ w3a 1037   = wceq 1483   e. wcel 1990   =/= wne 2794   class class class wbr 4653   ` cfv 5888  (class class class)co 6650   CCcc 9934   RRcr 9935   0cc0 9936   1c1 9937   _ici 9938   + caddc 9939   x. cmul 9941   <_ cle 10075   - cmin 10266   -ucneg 10267   / cdiv 10684   2c2 11070   4c4 11072   NN0cn0 11292   ^cexp 12860   sqrcsqrt 13973   abscabs 13974   NrmCVeccnv 27439   +vcpv 27440   BaseSetcba 27441   .sOLDcns 27442   0veccn0v 27443   norm_CVcnmcv 27445   .iOLDcdip 27555

This theorem was proved from axioms:  ax-mp 5  ax-1 6  ax-2 7  ax-3 8  ax-gen 1722  ax-4 1737  ax-5 1839  ax-6 1888  ax-7 1935  ax-8 1992  ax-9 1999  ax-10 2019  ax-11 2034  ax-12 2047  ax-13 2246  ax-ext 2602  ax-rep 4771  ax-sep 4781  ax-nul 4789  ax-pow 4843  ax-pr 4906  ax-un 6949  ax-inf2 8538  ax-cnex 9992  ax-resscn 9993  ax-1cn 9994  ax-icn 9995  ax-addcl 9996  ax-addrcl 9997  ax-mulcl 9998  ax-mulrcl 9999  ax-mulcom 10000  ax-addass 10001  ax-mulass 10002  ax-distr 10003  ax-i2m1 10004  ax-1ne0 10005  ax-1rid 10006  ax-rnegex 10007  ax-rrecex 10008  ax-cnre 10009  ax-pre-lttri 10010  ax-pre-lttrn 10011  ax-pre-ltadd 10012  ax-pre-mulgt0 10013  ax-pre-sup 10014

This theorem depends on definitions:  df-bi 197  df-or 385  df-an 386  df-3or 1038  df-3an 1039  df-tru 1486  df-fal 1489  df-ex 1705  df-nf 1710  df-sb 1881  df-eu 2474  df-mo 2475  df-clab 2609  df-cleq 2615  df-clel 2618  df-nfc 2753  df-ne 2795  df-nel 2898  df-ral 2917  df-rex 2918  df-reu 2919  df-rmo 2920  df-rab 2921  df-v 3202  df-sbc 3436  df-csb 3534  df-dif 3577  df-un 3579  df-in 3581  df-ss 3588  df-pss 3590  df-nul 3916  df-if 4087  df-pw 4160  df-sn 4178  df-pr 4180  df-tp 4182  df-op 4184  df-uni 4437  df-int 4476  df-iun 4522  df-br 4654  df-opab 4713  df-mpt 4730  df-tr 4753  df-id 5024  df-eprel 5029  df-po 5035  df-so 5036  df-fr 5073  df-se 5074  df-we 5075  df-xp 5120  df-rel 5121  df-cnv 5122  df-co 5123  df-dm 5124  df-rn 5125  df-res 5126  df-ima 5127  df-pred 5680  df-ord 5726  df-on 5727  df-lim 5728  df-suc 5729  df-iota 5851  df-fun 5890  df-fn 5891  df-f 5892  df-f1 5893  df-fo 5894  df-f1o 5895  df-fv 5896  df-isom 5897  df-riota 6611  df-ov 6653  df-oprab 6654  df-mpt2 6655  df-om 7066  df-1st 7168  df-2nd 7169  df-wrecs 7407  df-recs 7468  df-rdg 7506  df-1o 7560  df-oadd 7564  df-er 7742  df-en 7956  df-dom 7957  df-sdom 7958  df-fin 7959  df-sup 8348  df-oi 8415  df-card 8765  df-pnf 10076  df-mnf 10077  df-xr 10078  df-ltxr 10079  df-le 10080  df-sub 10268  df-neg 10269  df-div 10685  df-nn 11021  df-2 11079  df-3 11080  df-4 11081  df-n0 11293  df-z 11378  df-uz 11688  df-rp 11833  df-fz 12327  df-fzo 12466  df-seq 12802  df-exp 12861  df-hash 13118  df-cj 13839  df-re 13840  df-im 13841  df-sqrt 13975  df-abs 13976  df-clim 14219  df-sum 14417  df-grpo 27347  df-gid 27348  df-ginv 27349  df-ablo 27399  df-vc 27414  df-nv 27447  df-va 27450  df-ba 27451  df-sm 27452  df-0v 27453  df-nmcv 27455  df-dip 27556

This theorem is referenced by:  ipnm  27566  ipz  27574  pythi  27705  siilem1  27706  hlipgt0  27770  htthlem  27774