| Step | Hyp | Ref
| Expression |
|---|
| 1 | | rrxval.r |
. . . 4
    ℝ^ ℝ^   |
| 2 | 1 | rrxval 23175 |
. . 3
         toCHil toCHil  RRfld freeLMod RRfld freeLMod     |
| 3 | 2 | fveq2d 6195 |
. 2
                toCHil toCHil  RRfld freeLMod RRfld freeLMod      |
| 4 | | recrng 19967 |
. . . . 5
 RRfld RRfld  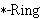 |
| 5 | | srngring 18852 |
. . . . 5
  RRfld RRfld  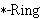  RRfld RRfld    |
| 6 | 4, 5 | ax-mp 5 |
. . . 4
 RRfld RRfld   |
| 7 | | eqid 2622 |
. . . . 5
  RRfld freeLMod RRfld freeLMod     RRfld
freeLMod RRfld
freeLMod   |
| 8 | 7 | frlmlmod 20093 |
. . . 4
   RRfld RRfld   
      RRfld freeLMod RRfld freeLMod      |
| 9 | 6, 8 | mpan 706 |
. . 3
       RRfld freeLMod RRfld freeLMod      |
| 10 | | lmodgrp 18870 |
. . 3
   RRfld freeLMod RRfld freeLMod       RRfld freeLMod RRfld freeLMod      |
| 11 | | eqid 2622 |
. . . 4
  toCHil toCHil  RRfld freeLMod RRfld freeLMod      toCHil toCHil  RRfld freeLMod RRfld freeLMod    |
| 12 | | eqid 2622 |
. . . 4
     toCHil toCHil  RRfld freeLMod RRfld freeLMod          toCHil toCHil  RRfld freeLMod RRfld freeLMod     |
| 13 | | eqid 2622 |
. . . 4
     RRfld freeLMod RRfld freeLMod         RRfld freeLMod RRfld freeLMod    |
| 14 | 11, 12, 13 | tchds 23030 |
. . 3
   RRfld freeLMod RRfld freeLMod           toCHil toCHil  RRfld freeLMod RRfld freeLMod          RRfld freeLMod RRfld freeLMod          toCHil toCHil  RRfld freeLMod RRfld freeLMod      |
| 15 | 9, 10, 14 | 3syl 18 |
. 2
           toCHil toCHil  RRfld freeLMod RRfld freeLMod          RRfld freeLMod RRfld freeLMod          toCHil toCHil  RRfld freeLMod RRfld freeLMod      |
| 16 | | eqid 2622 |
. . . . . . . 8
     RRfld freeLMod RRfld freeLMod         RRfld freeLMod RRfld freeLMod    |
| 17 | 16, 13 | grpsubf 17494 |
. . . . . . 7
   RRfld freeLMod RRfld freeLMod          RRfld freeLMod RRfld freeLMod          RRfld freeLMod RRfld freeLMod         RRfld freeLMod RRfld freeLMod          RRfld freeLMod RRfld freeLMod     |
| 18 | 9, 10, 17 | 3syl 18 |
. . . . . 6
          RRfld
freeLMod RRfld
freeLMod          RRfld freeLMod RRfld freeLMod         RRfld freeLMod RRfld freeLMod          RRfld freeLMod RRfld freeLMod     |
| 19 | | rrxbase.b |
. . . . . . . . . 10
        |
| 20 | 1, 19 | rrxbase 23176 |
. . . . . . . . 9
                  finSupp finSupp
   |
| 21 | | rebase 19952 |
. . . . . . . . . . 11
      RRfld RRfld |
| 22 | | re0g 19958 |
. . . . . . . . . . 11
      RRfld RRfld |
| 23 | | eqid 2622 |
. . . . . . . . . . 11
           finSupp finSupp   
          finSupp finSupp   |
| 24 | 7, 21, 22, 23 | frlmbas 20099 |
. . . . . . . . . 10
   RRfld RRfld   
               finSupp finSupp   
    RRfld freeLMod RRfld freeLMod     |
| 25 | 6, 24 | mpan 706 |
. . . . . . . . 9
                finSupp finSupp   
    RRfld freeLMod RRfld freeLMod     |
| 26 | 20, 25 | eqtrd 2656 |
. . . . . . . 8
            RRfld freeLMod RRfld freeLMod     |
| 27 | 26 | sqxpeqd 5141 |
. . . . . . 7
                 RRfld freeLMod RRfld freeLMod         RRfld
freeLMod RRfld
freeLMod      |
| 28 | 27, 26 | feq23d 6040 |
. . . . . 6
           RRfld freeLMod RRfld freeLMod                 RRfld freeLMod RRfld freeLMod          RRfld freeLMod RRfld freeLMod         RRfld freeLMod RRfld freeLMod          RRfld freeLMod RRfld freeLMod      |
| 29 | 18, 28 | mpbird 247 |
. . . . 5
          RRfld
freeLMod RRfld
freeLMod             |
| 30 | 29 | fovrnda 6805 |
. . . 4
            
           RRfld freeLMod RRfld freeLMod         |
| 31 | | ffn 6045 |
. . . . . 6
      RRfld freeLMod RRfld freeLMod                 RRfld freeLMod RRfld freeLMod           |
| 32 | 29, 31 | syl 17 |
. . . . 5
          RRfld
freeLMod RRfld
freeLMod           |
| 33 | | fnov 6768 |
. . . . 5
      RRfld freeLMod RRfld freeLMod          
    RRfld freeLMod RRfld freeLMod          
         RRfld freeLMod RRfld freeLMod        |
| 34 | 32, 33 | sylib 208 |
. . . 4
          RRfld
freeLMod RRfld
freeLMod                    RRfld freeLMod RRfld freeLMod        |
| 35 | 1, 19 | rrxnm 23179 |
. . . . 5
               RRfld RRfld  g g                          |
| 36 | 2 | fveq2d 6195 |
. . . . 5
                toCHil toCHil  RRfld freeLMod RRfld freeLMod      |
| 37 | 35, 36 | eqtr2d 2657 |
. . . 4
          toCHil toCHil  RRfld freeLMod RRfld freeLMod               RRfld RRfld  g g                    |
| 38 | | fveq1 6190 |
. . . . . . . 8
          RRfld freeLMod RRfld freeLMod                    RRfld freeLMod RRfld freeLMod          |
| 39 | 38 | oveq1d 6665 |
. . . . . . 7
          RRfld freeLMod RRfld freeLMod                         RRfld freeLMod RRfld freeLMod             |
| 40 | 39 | mpteq2dv 4745 |
. . . . . 6
          RRfld freeLMod RRfld freeLMod                                    RRfld freeLMod RRfld freeLMod              |
| 41 | 40 | oveq2d 6666 |
. . . . 5
          RRfld freeLMod RRfld freeLMod        RRfld RRfld  g g                   RRfld RRfld  g g              RRfld freeLMod RRfld freeLMod               |
| 42 | 41 | fveq2d 6195 |
. . . 4
          RRfld freeLMod RRfld freeLMod           RRfld RRfld  g g                       RRfld RRfld  g g              RRfld freeLMod RRfld freeLMod                |
| 43 | 30, 34, 37, 42 | fmpt2co 7260 |
. . 3
           toCHil toCHil  RRfld freeLMod RRfld freeLMod          RRfld freeLMod RRfld freeLMod           
       RRfld RRfld  g g              RRfld freeLMod RRfld freeLMod                 |
| 44 | | simp1 1061 |
. . . . . . . . . . . . . 14
        
   
       |
| 45 | | simprl 794 |
. . . . . . . . . . . . . . . 16
            
         |
| 46 | 26 | adantr 481 |
. . . . . . . . . . . . . . . 16
            
           RRfld freeLMod RRfld freeLMod     |
| 47 | 45, 46 | eleqtrd 2703 |
. . . . . . . . . . . . . . 15
            
           RRfld freeLMod RRfld freeLMod     |
| 48 | 47 | 3impb 1260 |
. . . . . . . . . . . . . 14
        
   
         RRfld freeLMod RRfld freeLMod     |
| 49 | 7, 21, 16 | frlmbasmap 20103 |
. . . . . . . . . . . . . 14
        
    RRfld freeLMod RRfld freeLMod              |
| 50 | 44, 48, 49 | syl2anc 693 |
. . . . . . . . . . . . 13
        
   
           |
| 51 | | elmapi 7879 |
. . . . . . . . . . . . 13
                |
| 52 | 50, 51 | syl 17 |
. . . . . . . . . . . 12
        
   
         |
| 53 | | ffn 6045 |
. . . . . . . . . . . 12
            |
| 54 | 52, 53 | syl 17 |
. . . . . . . . . . 11
        
   
       |
| 55 | | simprr 796 |
. . . . . . . . . . . . . . . 16
            
         |
| 56 | 55, 46 | eleqtrd 2703 |
. . . . . . . . . . . . . . 15
            
           RRfld freeLMod RRfld freeLMod     |
| 57 | 56 | 3impb 1260 |
. . . . . . . . . . . . . 14
        
   
         RRfld freeLMod RRfld freeLMod     |
| 58 | 7, 21, 16 | frlmbasmap 20103 |
. . . . . . . . . . . . . 14
        
    RRfld freeLMod RRfld freeLMod              |
| 59 | 44, 57, 58 | syl2anc 693 |
. . . . . . . . . . . . 13
        
   
           |
| 60 | | elmapi 7879 |
. . . . . . . . . . . . 13
                |
| 61 | 59, 60 | syl 17 |
. . . . . . . . . . . 12
        
   
         |
| 62 | | ffn 6045 |
. . . . . . . . . . . 12
            |
| 63 | 61, 62 | syl 17 |
. . . . . . . . . . 11
        
   
       |
| 64 | | inidm 3822 |
. . . . . . . . . . 11
        |
| 65 | | eqidd 2623 |
. . . . . . . . . . 11
        
   
   
                 |
| 66 | | eqidd 2623 |
. . . . . . . . . . 11
        
   
   
                 |
| 67 | 54, 63, 44, 44, 64, 65, 66 | offval 6904 |
. . . . . . . . . 10
        
   
          RRfld RRfld                  RRfld RRfld         |
| 68 | 6 | a1i 11 |
. . . . . . . . . . . 12
            
     RRfld RRfld    |
| 69 | | simpl 473 |
. . . . . . . . . . . 12
            
         |
| 70 | | eqid 2622 |
. . . . . . . . . . . 12
    RRfld RRfld     RRfld RRfld |
| 71 | 7, 16, 68, 69, 47, 56, 70, 13 | frlmsubgval 20108 |
. . . . . . . . . . 11
            
           RRfld freeLMod RRfld freeLMod              RRfld RRfld    |
| 72 | 71 | 3impb 1260 |
. . . . . . . . . 10
        
   
         RRfld freeLMod RRfld freeLMod              RRfld RRfld    |
| 73 | 52 | ffvelrnda 6359 |
. . . . . . . . . . . 12
        
   
   
             |
| 74 | 61 | ffvelrnda 6359 |
. . . . . . . . . . . 12
        
   
   
             |
| 75 | 70 | resubgval 19955 |
. . . . . . . . . . . 12
                                           RRfld RRfld        |
| 76 | 73, 74, 75 | syl2anc 693 |
. . . . . . . . . . 11
        
   
   
                            RRfld RRfld        |
| 77 | 76 | mpteq2dva 4744 |
. . . . . . . . . 10
        
   
                                     RRfld RRfld         |
| 78 | 67, 72, 77 | 3eqtr4d 2666 |
. . . . . . . . 9
        
   
         RRfld freeLMod RRfld freeLMod                           |
| 79 | 73, 74 | resubcld 10458 |
. . . . . . . . 9
        
   
   
                     |
| 80 | 78, 79 | fvmpt2d 6293 |
. . . . . . . 8
        
   
   
            RRfld freeLMod RRfld freeLMod                        |
| 81 | 80 | oveq1d 6665 |
. . . . . . 7
        
   
   
             RRfld freeLMod RRfld freeLMod                               |
| 82 | 81 | mpteq2dva 4744 |
. . . . . 6
        
   
                RRfld freeLMod RRfld freeLMod                                      |
| 83 | 82 | oveq2d 6666 |
. . . . 5
        
   
    RRfld RRfld  g g              RRfld freeLMod RRfld freeLMod                RRfld RRfld  g g                          |
| 84 | 83 | fveq2d 6195 |
. . . 4
        
   
       RRfld RRfld  g g              RRfld freeLMod RRfld freeLMod                    RRfld RRfld  g g                           |
| 85 | 84 | mpt2eq3dva 6719 |
. . 3
                   RRfld RRfld  g g              RRfld freeLMod RRfld freeLMod                      
       RRfld RRfld  g g                            |
| 86 | 43, 85 | eqtrd 2656 |
. 2
           toCHil toCHil  RRfld freeLMod RRfld freeLMod          RRfld freeLMod RRfld freeLMod           
       RRfld RRfld  g g                            |
| 87 | 3, 15, 86 | 3eqtr2rd 2663 |
1
                   RRfld RRfld  g g                                  |