Theorem minvecolem3 27732

Description: Lemma for minveco 27740. The sequence formed by taking elements successively closer to the infimum is Cauchy. (Contributed by Mario Carneiro, 8-May-2014.) (Revised by AV, 4-Oct-2020.) (New usage is discouraged.)

Hypotheses

Ref	Expression
minveco.x	|- X = ( BaseSet ` U )
minveco.m	|- M = ( -v ` U )
minveco.n	|- N = ( normCV ` U )
minveco.y	|- Y = ( BaseSet ` W )
minveco.u	|- ( ph -> U e. CPreHil OLD )
minveco.w	|- ( ph -> W e. ( ( SubSp ` U ) i^i CBan ) )
minveco.a	|- ( ph -> A e. X )
minveco.d	|- D = ( IndMet ` U )
minveco.j	|- J = ( MetOpen ` D )
minveco.r	|- R = ran ( y e. Y |-> ( N ` ( A M y ) ) )
minveco.s	|- S = inf ( R , RR , < )
minveco.f	|- ( ph -> F : NN --> Y )
minveco.1	|- ( ( ph /\ n e. NN ) -> ( ( A D ( F ` n ) ) ^ 2 ) <_ ( ( S ^ 2 ) + ( 1 / n ) ) )

Assertion

Ref	Expression
minvecolem3	|- ( ph -> F e. ( Cau ` D ) )

Distinct variable groups:   y, n, F   n, J, y   y, M   y, N   ph, n, y   S, n, y   A, n, y   D, n, y   y, U   y, W   n, X   n, Y, y

Allowed substitution hints:   R( y, n)   U( n)   M( n)   N( n)   W( n)   X( y)

Proof of Theorem minvecolem3

Dummy variables j x w are mutually distinct and distinct from all other variables.

Step	Hyp	Ref	Expression
1		4re 11097	. . . . . . 7 |- 4 e. RR
2		4pos 11116	. . . . . . 7 |- 0 < 4
3	1, 2	elrpii 11835	. . . . . 6 |- 4 e. RR+
4		simpr 477	. . . . . . 7 |- ( ( ph /\ x e. RR+ ) -> x e. RR+ )
5		2z 11409	. . . . . . 7 |- 2 e. ZZ
6		rpexpcl 12879	. . . . . . 7 |- ( ( x e. RR+ /\ 2 e. ZZ ) -> ( x ^ 2 ) e. RR+ )
7	4, 5, 6	sylancl 694	. . . . . 6 |- ( ( ph /\ x e. RR+ ) -> ( x ^ 2 ) e. RR+ )
8		rpdivcl 11856	. . . . . 6 |- ( ( 4 e. RR+ /\ ( x ^ 2 ) e. RR+ ) -> ( 4 / ( x ^ 2 ) ) e. RR+ )
9	3, 7, 8	sylancr 695	. . . . 5 |- ( ( ph /\ x e. RR+ ) -> ( 4 / ( x ^ 2 ) ) e. RR+ )
10		rprege0 11847	. . . . 5 |- ( ( 4 / ( x ^ 2 ) ) e. RR+ -> ( ( 4 / ( x ^ 2 ) ) e. RR /\ 0 <_ ( 4 / ( x ^ 2 ) ) ) )
11		flge0nn0 12621	. . . . 5 |- ( ( ( 4 / ( x ^ 2 ) ) e. RR /\ 0 <_ ( 4 / ( x ^ 2 ) ) ) -> ( |_ ` ( 4 / ( x ^ 2 ) ) ) e. NN0 )
12		nn0p1nn 11332	. . . . 5 |- ( ( |_ ` ( 4 / ( x ^ 2 ) ) ) e. NN0 -> ( ( |_ ` ( 4 / ( x ^ 2 ) ) ) + 1 ) e. NN )
13	9, 10, 11, 12	4syl 19	. . . 4 |- ( ( ph /\ x e. RR+ ) -> ( ( |_ ` ( 4 / ( x ^ 2 ) ) ) + 1 ) e. NN )
14		minveco.u	. . . . . . . . . . 11 |- ( ph -> U e. CPreHil OLD )
15		phnv 27669	. . . . . . . . . . 11 |- ( U e. CPreHil OLD -> U e. NrmCVec )
16		minveco.x	. . . . . . . . . . . 12 |- X = ( BaseSet ` U )
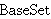17		minveco.d	. . . . . . . . . . . 12 |- D = ( IndMet ` U )
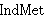18	16, 17	imsmet 27546	. . . . . . . . . . 11 |- ( U e. NrmCVec -> D e. ( Met ` X ) )
19	14, 15, 18	3syl 18	. . . . . . . . . 10 |- ( ph -> D e. ( Met ` X ) )
20	19	ad2antrr 762	. . . . . . . . 9 |- ( ( ( ph /\ x e. RR+ ) /\ n e. ( ZZ>= ` ( ( |_ ` ( 4 / ( x ^ 2 ) ) ) + 1 ) ) ) -> D e. ( Met ` X ) )
21	14, 15	syl 17	. . . . . . . . . . . 12 |- ( ph -> U e. NrmCVec )
22		inss1 3833	. . . . . . . . . . . . 13 |- ( ( SubSp ` U ) i^i CBan ) C_ ( SubSp ` U )
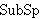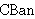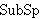23		minveco.w	. . . . . . . . . . . . 13 |- ( ph -> W e. ( ( SubSp ` U ) i^i CBan ) )
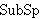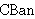24	22, 23	sseldi 3601	. . . . . . . . . . . 12 |- ( ph -> W e. ( SubSp ` U ) )
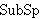25		minveco.y	. . . . . . . . . . . . 13 |- Y = ( BaseSet ` W )
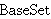26		eqid 2622	. . . . . . . . . . . . 13 |- ( SubSp ` U ) = ( SubSp ` U )
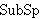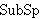27	16, 25, 26	sspba 27582	. . . . . . . . . . . 12 |- ( ( U e. NrmCVec /\ W e. ( SubSp ` U ) ) -> Y C_ X )
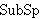
28	21, 24, 27	syl2anc 693	. . . . . . . . . . 11 |- ( ph -> Y C_ X )
29	28	ad2antrr 762	. . . . . . . . . 10 |- ( ( ( ph /\ x e. RR+ ) /\ n e. ( ZZ>= ` ( ( |_ ` ( 4 / ( x ^ 2 ) ) ) + 1 ) ) ) -> Y C_ X )
30		minveco.f	. . . . . . . . . . . 12 |- ( ph -> F : NN --> Y )
31	30	ad2antrr 762	. . . . . . . . . . 11 |- ( ( ( ph /\ x e. RR+ ) /\ n e. ( ZZ>= ` ( ( |_ ` ( 4 / ( x ^ 2 ) ) ) + 1 ) ) ) -> F : NN --> Y )
32	13	adantr 481	. . . . . . . . . . 11 |- ( ( ( ph /\ x e. RR+ ) /\ n e. ( ZZ>= ` ( ( |_ ` ( 4 / ( x ^ 2 ) ) ) + 1 ) ) ) -> ( ( |_ ` ( 4 / ( x ^ 2 ) ) ) + 1 ) e. NN )
33	31, 32	ffvelrnd 6360	. . . . . . . . . 10 |- ( ( ( ph /\ x e. RR+ ) /\ n e. ( ZZ>= ` ( ( |_ ` ( 4 / ( x ^ 2 ) ) ) + 1 ) ) ) -> ( F ` ( ( |_ ` ( 4 / ( x ^ 2 ) ) ) + 1 ) ) e. Y )
34	29, 33	sseldd 3604	. . . . . . . . 9 |- ( ( ( ph /\ x e. RR+ ) /\ n e. ( ZZ>= ` ( ( |_ ` ( 4 / ( x ^ 2 ) ) ) + 1 ) ) ) -> ( F ` ( ( |_ ` ( 4 / ( x ^ 2 ) ) ) + 1 ) ) e. X )
35		eluznn 11758	. . . . . . . . . . . 12 |- ( ( ( ( |_ ` ( 4 / ( x ^ 2 ) ) ) + 1 ) e. NN /\ n e. ( ZZ>= ` ( ( |_ ` ( 4 / ( x ^ 2 ) ) ) + 1 ) ) ) -> n e. NN )
36	13, 35	sylan 488	. . . . . . . . . . 11 |- ( ( ( ph /\ x e. RR+ ) /\ n e. ( ZZ>= ` ( ( |_ ` ( 4 / ( x ^ 2 ) ) ) + 1 ) ) ) -> n e. NN )
37	31, 36	ffvelrnd 6360	. . . . . . . . . 10 |- ( ( ( ph /\ x e. RR+ ) /\ n e. ( ZZ>= ` ( ( |_ ` ( 4 / ( x ^ 2 ) ) ) + 1 ) ) ) -> ( F ` n ) e. Y )
38	29, 37	sseldd 3604	. . . . . . . . 9 |- ( ( ( ph /\ x e. RR+ ) /\ n e. ( ZZ>= ` ( ( |_ ` ( 4 / ( x ^ 2 ) ) ) + 1 ) ) ) -> ( F ` n ) e. X )
39		metcl 22137	. . . . . . . . 9 |- ( ( D e. ( Met ` X ) /\ ( F ` ( ( |_ ` ( 4 / ( x ^ 2 ) ) ) + 1 ) ) e. X /\ ( F ` n ) e. X ) -> ( ( F ` ( ( |_ ` ( 4 / ( x ^ 2 ) ) ) + 1 ) ) D ( F ` n ) ) e. RR )
40	20, 34, 38, 39	syl3anc 1326	. . . . . . . 8 |- ( ( ( ph /\ x e. RR+ ) /\ n e. ( ZZ>= ` ( ( |_ ` ( 4 / ( x ^ 2 ) ) ) + 1 ) ) ) -> ( ( F ` ( ( |_ ` ( 4 / ( x ^ 2 ) ) ) + 1 ) ) D ( F ` n ) ) e. RR )
41	40	resqcld 13035	. . . . . . 7 |- ( ( ( ph /\ x e. RR+ ) /\ n e. ( ZZ>= ` ( ( |_ ` ( 4 / ( x ^ 2 ) ) ) + 1 ) ) ) -> ( ( ( F ` ( ( |_ ` ( 4 / ( x ^ 2 ) ) ) + 1 ) ) D ( F ` n ) ) ^ 2 ) e. RR )
42	32	nnrpd 11870	. . . . . . . . . 10 |- ( ( ( ph /\ x e. RR+ ) /\ n e. ( ZZ>= ` ( ( |_ ` ( 4 / ( x ^ 2 ) ) ) + 1 ) ) ) -> ( ( |_ ` ( 4 / ( x ^ 2 ) ) ) + 1 ) e. RR+ )
43	42	rpreccld 11882	. . . . . . . . 9 |- ( ( ( ph /\ x e. RR+ ) /\ n e. ( ZZ>= ` ( ( |_ ` ( 4 / ( x ^ 2 ) ) ) + 1 ) ) ) -> ( 1 / ( ( |_ ` ( 4 / ( x ^ 2 ) ) ) + 1 ) ) e. RR+ )
44		rpmulcl 11855	. . . . . . . . 9 |- ( ( 4 e. RR+ /\ ( 1 / ( ( |_ ` ( 4 / ( x ^ 2 ) ) ) + 1 ) ) e. RR+ ) -> ( 4 x. ( 1 / ( ( |_ ` ( 4 / ( x ^ 2 ) ) ) + 1 ) ) ) e. RR+ )
45	3, 43, 44	sylancr 695	. . . . . . . 8 |- ( ( ( ph /\ x e. RR+ ) /\ n e. ( ZZ>= ` ( ( |_ ` ( 4 / ( x ^ 2 ) ) ) + 1 ) ) ) -> ( 4 x. ( 1 / ( ( |_ ` ( 4 / ( x ^ 2 ) ) ) + 1 ) ) ) e. RR+ )
46	45	rpred 11872	. . . . . . 7 |- ( ( ( ph /\ x e. RR+ ) /\ n e. ( ZZ>= ` ( ( |_ ` ( 4 / ( x ^ 2 ) ) ) + 1 ) ) ) -> ( 4 x. ( 1 / ( ( |_ ` ( 4 / ( x ^ 2 ) ) ) + 1 ) ) ) e. RR )
47	7	adantr 481	. . . . . . . 8 |- ( ( ( ph /\ x e. RR+ ) /\ n e. ( ZZ>= ` ( ( |_ ` ( 4 / ( x ^ 2 ) ) ) + 1 ) ) ) -> ( x ^ 2 ) e. RR+ )
48	47	rpred 11872	. . . . . . 7 |- ( ( ( ph /\ x e. RR+ ) /\ n e. ( ZZ>= ` ( ( |_ ` ( 4 / ( x ^ 2 ) ) ) + 1 ) ) ) -> ( x ^ 2 ) e. RR )
49		minveco.m	. . . . . . . 8 |- M = ( -v ` U )
50		minveco.n	. . . . . . . 8 |- N = ( normCV ` U )
51	14	ad2antrr 762	. . . . . . . 8 |- ( ( ( ph /\ x e. RR+ ) /\ n e. ( ZZ>= ` ( ( |_ ` ( 4 / ( x ^ 2 ) ) ) + 1 ) ) ) -> U e. CPreHil OLD )
52	23	ad2antrr 762	. . . . . . . 8 |- ( ( ( ph /\ x e. RR+ ) /\ n e. ( ZZ>= ` ( ( |_ ` ( 4 / ( x ^ 2 ) ) ) + 1 ) ) ) -> W e. ( ( SubSp ` U ) i^i CBan ) )
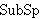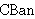53		minveco.a	. . . . . . . . 9 |- ( ph -> A e. X )
54	53	ad2antrr 762	. . . . . . . 8 |- ( ( ( ph /\ x e. RR+ ) /\ n e. ( ZZ>= ` ( ( |_ ` ( 4 / ( x ^ 2 ) ) ) + 1 ) ) ) -> A e. X )
55		minveco.j	. . . . . . . 8 |- J = ( MetOpen ` D )
56		minveco.r	. . . . . . . 8 |- R = ran ( y e. Y |-> ( N ` ( A M y ) ) )
57		minveco.s	. . . . . . . 8 |- S = inf ( R , RR , < )
58	13	nnrpd 11870	. . . . . . . . . . 11 |- ( ( ph /\ x e. RR+ ) -> ( ( |_ ` ( 4 / ( x ^ 2 ) ) ) + 1 ) e. RR+ )
59	58	rpreccld 11882	. . . . . . . . . 10 |- ( ( ph /\ x e. RR+ ) -> ( 1 / ( ( |_ ` ( 4 / ( x ^ 2 ) ) ) + 1 ) ) e. RR+ )
60	59	adantr 481	. . . . . . . . 9 |- ( ( ( ph /\ x e. RR+ ) /\ n e. ( ZZ>= ` ( ( |_ ` ( 4 / ( x ^ 2 ) ) ) + 1 ) ) ) -> ( 1 / ( ( |_ ` ( 4 / ( x ^ 2 ) ) ) + 1 ) ) e. RR+ )
61	60	rpred 11872	. . . . . . . 8 |- ( ( ( ph /\ x e. RR+ ) /\ n e. ( ZZ>= ` ( ( |_ ` ( 4 / ( x ^ 2 ) ) ) + 1 ) ) ) -> ( 1 / ( ( |_ ` ( 4 / ( x ^ 2 ) ) ) + 1 ) ) e. RR )
62	60	rpge0d 11876	. . . . . . . 8 |- ( ( ( ph /\ x e. RR+ ) /\ n e. ( ZZ>= ` ( ( |_ ` ( 4 / ( x ^ 2 ) ) ) + 1 ) ) ) -> 0 <_ ( 1 / ( ( |_ ` ( 4 / ( x ^ 2 ) ) ) + 1 ) ) )
63	30	adantr 481	. . . . . . . . . 10 |- ( ( ph /\ x e. RR+ ) -> F : NN --> Y )
64	63	ffvelrnda 6359	. . . . . . . . 9 |- ( ( ( ph /\ x e. RR+ ) /\ n e. NN ) -> ( F ` n ) e. Y )
65	36, 64	syldan 487	. . . . . . . 8 |- ( ( ( ph /\ x e. RR+ ) /\ n e. ( ZZ>= ` ( ( |_ ` ( 4 / ( x ^ 2 ) ) ) + 1 ) ) ) -> ( F ` n ) e. Y )
66		minveco.1	. . . . . . . . . . 11 |- ( ( ph /\ n e. NN ) -> ( ( A D ( F ` n ) ) ^ 2 ) <_ ( ( S ^ 2 ) + ( 1 / n ) ) )
67	66	ralrimiva 2966	. . . . . . . . . 10 |- ( ph -> A. n e. NN ( ( A D ( F ` n ) ) ^ 2 ) <_ ( ( S ^ 2 ) + ( 1 / n ) ) )
68	67	ad2antrr 762	. . . . . . . . 9 |- ( ( ( ph /\ x e. RR+ ) /\ n e. ( ZZ>= ` ( ( |_ ` ( 4 / ( x ^ 2 ) ) ) + 1 ) ) ) -> A. n e. NN ( ( A D ( F ` n ) ) ^ 2 ) <_ ( ( S ^ 2 ) + ( 1 / n ) ) )
69		fveq2 6191	. . . . . . . . . . . . 13 |- ( n = ( ( |_ ` ( 4 / ( x ^ 2 ) ) ) + 1 ) -> ( F ` n ) = ( F ` ( ( |_ ` ( 4 / ( x ^ 2 ) ) ) + 1 ) ) )
70	69	oveq2d 6666	. . . . . . . . . . . 12 |- ( n = ( ( |_ ` ( 4 / ( x ^ 2 ) ) ) + 1 ) -> ( A D ( F ` n ) ) = ( A D ( F ` ( ( |_ ` ( 4 / ( x ^ 2 ) ) ) + 1 ) ) ) )
71	70	oveq1d 6665	. . . . . . . . . . 11 |- ( n = ( ( |_ ` ( 4 / ( x ^ 2 ) ) ) + 1 ) -> ( ( A D ( F ` n ) ) ^ 2 ) = ( ( A D ( F ` ( ( |_ ` ( 4 / ( x ^ 2 ) ) ) + 1 ) ) ) ^ 2 ) )
72		oveq2 6658	. . . . . . . . . . . 12 |- ( n = ( ( |_ ` ( 4 / ( x ^ 2 ) ) ) + 1 ) -> ( 1 / n ) = ( 1 / ( ( |_ ` ( 4 / ( x ^ 2 ) ) ) + 1 ) ) )
73	72	oveq2d 6666	. . . . . . . . . . 11 |- ( n = ( ( |_ ` ( 4 / ( x ^ 2 ) ) ) + 1 ) -> ( ( S ^ 2 ) + ( 1 / n ) ) = ( ( S ^ 2 ) + ( 1 / ( ( |_ ` ( 4 / ( x ^ 2 ) ) ) + 1 ) ) ) )
74	71, 73	breq12d 4666	. . . . . . . . . 10 |- ( n = ( ( |_ ` ( 4 / ( x ^ 2 ) ) ) + 1 ) -> ( ( ( A D ( F ` n ) ) ^ 2 ) <_ ( ( S ^ 2 ) + ( 1 / n ) ) <-> ( ( A D ( F ` ( ( |_ ` ( 4 / ( x ^ 2 ) ) ) + 1 ) ) ) ^ 2 ) <_ ( ( S ^ 2 ) + ( 1 / ( ( |_ ` ( 4 / ( x ^ 2 ) ) ) + 1 ) ) ) ) )
75	74	rspcv 3305	. . . . . . . . 9 |- ( ( ( |_ ` ( 4 / ( x ^ 2 ) ) ) + 1 ) e. NN -> ( A. n e. NN ( ( A D ( F ` n ) ) ^ 2 ) <_ ( ( S ^ 2 ) + ( 1 / n ) ) -> ( ( A D ( F ` ( ( |_ ` ( 4 / ( x ^ 2 ) ) ) + 1 ) ) ) ^ 2 ) <_ ( ( S ^ 2 ) + ( 1 / ( ( |_ ` ( 4 / ( x ^ 2 ) ) ) + 1 ) ) ) ) )
76	32, 68, 75	sylc 65	. . . . . . . 8 |- ( ( ( ph /\ x e. RR+ ) /\ n e. ( ZZ>= ` ( ( |_ ` ( 4 / ( x ^ 2 ) ) ) + 1 ) ) ) -> ( ( A D ( F ` ( ( |_ ` ( 4 / ( x ^ 2 ) ) ) + 1 ) ) ) ^ 2 ) <_ ( ( S ^ 2 ) + ( 1 / ( ( |_ ` ( 4 / ( x ^ 2 ) ) ) + 1 ) ) ) )
77	29, 65	sseldd 3604	. . . . . . . . . . 11 |- ( ( ( ph /\ x e. RR+ ) /\ n e. ( ZZ>= ` ( ( |_ ` ( 4 / ( x ^ 2 ) ) ) + 1 ) ) ) -> ( F ` n ) e. X )
78		metcl 22137	. . . . . . . . . . 11 |- ( ( D e. ( Met ` X ) /\ A e. X /\ ( F ` n ) e. X ) -> ( A D ( F ` n ) ) e. RR )
79	20, 54, 77, 78	syl3anc 1326	. . . . . . . . . 10 |- ( ( ( ph /\ x e. RR+ ) /\ n e. ( ZZ>= ` ( ( |_ ` ( 4 / ( x ^ 2 ) ) ) + 1 ) ) ) -> ( A D ( F ` n ) ) e. RR )
80	79	resqcld 13035	. . . . . . . . 9 |- ( ( ( ph /\ x e. RR+ ) /\ n e. ( ZZ>= ` ( ( |_ ` ( 4 / ( x ^ 2 ) ) ) + 1 ) ) ) -> ( ( A D ( F ` n ) ) ^ 2 ) e. RR )
81	16, 49, 50, 25, 14, 23, 53, 17, 55, 56	minvecolem1 27730	. . . . . . . . . . . . . 14 |- ( ph -> ( R C_ RR /\ R =/= (/) /\ A. w e. R 0 <_ w ) )
82		0re 10040	. . . . . . . . . . . . . . . 16 |- 0 e. RR
83		breq1 4656	. . . . . . . . . . . . . . . . . 18 |- ( x = 0 -> ( x <_ w <-> 0 <_ w ) )
84	83	ralbidv 2986	. . . . . . . . . . . . . . . . 17 |- ( x = 0 -> ( A. w e. R x <_ w <-> A. w e. R 0 <_ w ) )
85	84	rspcev 3309	. . . . . . . . . . . . . . . 16 |- ( ( 0 e. RR /\ A. w e. R 0 <_ w ) -> E. x e. RR A. w e. R x <_ w )
86	82, 85	mpan 706	. . . . . . . . . . . . . . 15 |- ( A. w e. R 0 <_ w -> E. x e. RR A. w e. R x <_ w )
87	86	3anim3i 1250	. . . . . . . . . . . . . 14 |- ( ( R C_ RR /\ R =/= (/) /\ A. w e. R 0 <_ w ) -> ( R C_ RR /\ R =/= (/) /\ E. x e. RR A. w e. R x <_ w ) )
88		infrecl 11005	. . . . . . . . . . . . . 14 |- ( ( R C_ RR /\ R =/= (/) /\ E. x e. RR A. w e. R x <_ w ) -> inf ( R , RR , < ) e. RR )
89	81, 87, 88	3syl 18	. . . . . . . . . . . . 13 |- ( ph -> inf ( R , RR , < ) e. RR )
90	57, 89	syl5eqel 2705	. . . . . . . . . . . 12 |- ( ph -> S e. RR )
91	90	resqcld 13035	. . . . . . . . . . 11 |- ( ph -> ( S ^ 2 ) e. RR )
92	91	ad2antrr 762	. . . . . . . . . 10 |- ( ( ( ph /\ x e. RR+ ) /\ n e. ( ZZ>= ` ( ( |_ ` ( 4 / ( x ^ 2 ) ) ) + 1 ) ) ) -> ( S ^ 2 ) e. RR )
93	36	nnrecred 11066	. . . . . . . . . 10 |- ( ( ( ph /\ x e. RR+ ) /\ n e. ( ZZ>= ` ( ( |_ ` ( 4 / ( x ^ 2 ) ) ) + 1 ) ) ) -> ( 1 / n ) e. RR )
94	92, 93	readdcld 10069	. . . . . . . . 9 |- ( ( ( ph /\ x e. RR+ ) /\ n e. ( ZZ>= ` ( ( |_ ` ( 4 / ( x ^ 2 ) ) ) + 1 ) ) ) -> ( ( S ^ 2 ) + ( 1 / n ) ) e. RR )
95	92, 61	readdcld 10069	. . . . . . . . 9 |- ( ( ( ph /\ x e. RR+ ) /\ n e. ( ZZ>= ` ( ( |_ ` ( 4 / ( x ^ 2 ) ) ) + 1 ) ) ) -> ( ( S ^ 2 ) + ( 1 / ( ( |_ ` ( 4 / ( x ^ 2 ) ) ) + 1 ) ) ) e. RR )
96	66	adantlr 751	. . . . . . . . . 10 |- ( ( ( ph /\ x e. RR+ ) /\ n e. NN ) -> ( ( A D ( F ` n ) ) ^ 2 ) <_ ( ( S ^ 2 ) + ( 1 / n ) ) )
97	36, 96	syldan 487	. . . . . . . . 9 |- ( ( ( ph /\ x e. RR+ ) /\ n e. ( ZZ>= ` ( ( |_ ` ( 4 / ( x ^ 2 ) ) ) + 1 ) ) ) -> ( ( A D ( F ` n ) ) ^ 2 ) <_ ( ( S ^ 2 ) + ( 1 / n ) ) )
98		eluzle 11700	. . . . . . . . . . . 12 |- ( n e. ( ZZ>= ` ( ( |_ ` ( 4 / ( x ^ 2 ) ) ) + 1 ) ) -> ( ( |_ ` ( 4 / ( x ^ 2 ) ) ) + 1 ) <_ n )
99	98	adantl 482	. . . . . . . . . . 11 |- ( ( ( ph /\ x e. RR+ ) /\ n e. ( ZZ>= ` ( ( |_ ` ( 4 / ( x ^ 2 ) ) ) + 1 ) ) ) -> ( ( |_ ` ( 4 / ( x ^ 2 ) ) ) + 1 ) <_ n )
100	42	rpregt0d 11878	. . . . . . . . . . . 12 |- ( ( ( ph /\ x e. RR+ ) /\ n e. ( ZZ>= ` ( ( |_ ` ( 4 / ( x ^ 2 ) ) ) + 1 ) ) ) -> ( ( ( |_ ` ( 4 / ( x ^ 2 ) ) ) + 1 ) e. RR /\ 0 < ( ( |_ ` ( 4 / ( x ^ 2 ) ) ) + 1 ) ) )
101		nnre 11027	. . . . . . . . . . . . . 14 |- ( n e. NN -> n e. RR )
102		nngt0 11049	. . . . . . . . . . . . . 14 |- ( n e. NN -> 0 < n )
103	101, 102	jca 554	. . . . . . . . . . . . 13 |- ( n e. NN -> ( n e. RR /\ 0 < n ) )
104	36, 103	syl 17	. . . . . . . . . . . 12 |- ( ( ( ph /\ x e. RR+ ) /\ n e. ( ZZ>= ` ( ( |_ ` ( 4 / ( x ^ 2 ) ) ) + 1 ) ) ) -> ( n e. RR /\ 0 < n ) )
105		lerec 10906	. . . . . . . . . . . 12 |- ( ( ( ( ( |_ ` ( 4 / ( x ^ 2 ) ) ) + 1 ) e. RR /\ 0 < ( ( |_ ` ( 4 / ( x ^ 2 ) ) ) + 1 ) ) /\ ( n e. RR /\ 0 < n ) ) -> ( ( ( |_ ` ( 4 / ( x ^ 2 ) ) ) + 1 ) <_ n <-> ( 1 / n ) <_ ( 1 / ( ( |_ ` ( 4 / ( x ^ 2 ) ) ) + 1 ) ) ) )
106	100, 104, 105	syl2anc 693	. . . . . . . . . . 11 |- ( ( ( ph /\ x e. RR+ ) /\ n e. ( ZZ>= ` ( ( |_ ` ( 4 / ( x ^ 2 ) ) ) + 1 ) ) ) -> ( ( ( |_ ` ( 4 / ( x ^ 2 ) ) ) + 1 ) <_ n <-> ( 1 / n ) <_ ( 1 / ( ( |_ ` ( 4 / ( x ^ 2 ) ) ) + 1 ) ) ) )
107	99, 106	mpbid 222	. . . . . . . . . 10 |- ( ( ( ph /\ x e. RR+ ) /\ n e. ( ZZ>= ` ( ( |_ ` ( 4 / ( x ^ 2 ) ) ) + 1 ) ) ) -> ( 1 / n ) <_ ( 1 / ( ( |_ ` ( 4 / ( x ^ 2 ) ) ) + 1 ) ) )
108	93, 61, 92, 107	leadd2dd 10642	. . . . . . . . 9 |- ( ( ( ph /\ x e. RR+ ) /\ n e. ( ZZ>= ` ( ( |_ ` ( 4 / ( x ^ 2 ) ) ) + 1 ) ) ) -> ( ( S ^ 2 ) + ( 1 / n ) ) <_ ( ( S ^ 2 ) + ( 1 / ( ( |_ ` ( 4 / ( x ^ 2 ) ) ) + 1 ) ) ) )
109	80, 94, 95, 97, 108	letrd 10194	. . . . . . . 8 |- ( ( ( ph /\ x e. RR+ ) /\ n e. ( ZZ>= ` ( ( |_ ` ( 4 / ( x ^ 2 ) ) ) + 1 ) ) ) -> ( ( A D ( F ` n ) ) ^ 2 ) <_ ( ( S ^ 2 ) + ( 1 / ( ( |_ ` ( 4 / ( x ^ 2 ) ) ) + 1 ) ) ) )
110	16, 49, 50, 25, 51, 52, 54, 17, 55, 56, 57, 61, 62, 33, 65, 76, 109	minvecolem2 27731	. . . . . . 7 |- ( ( ( ph /\ x e. RR+ ) /\ n e. ( ZZ>= ` ( ( |_ ` ( 4 / ( x ^ 2 ) ) ) + 1 ) ) ) -> ( ( ( F ` ( ( |_ ` ( 4 / ( x ^ 2 ) ) ) + 1 ) ) D ( F ` n ) ) ^ 2 ) <_ ( 4 x. ( 1 / ( ( |_ ` ( 4 / ( x ^ 2 ) ) ) + 1 ) ) ) )
111		rpdivcl 11856	. . . . . . . . . 10 |- ( ( ( x ^ 2 ) e. RR+ /\ 4 e. RR+ ) -> ( ( x ^ 2 ) / 4 ) e. RR+ )
112	47, 3, 111	sylancl 694	. . . . . . . . 9 |- ( ( ( ph /\ x e. RR+ ) /\ n e. ( ZZ>= ` ( ( |_ ` ( 4 / ( x ^ 2 ) ) ) + 1 ) ) ) -> ( ( x ^ 2 ) / 4 ) e. RR+ )
113		rpcnne0 11850	. . . . . . . . . . . 12 |- ( ( x ^ 2 ) e. RR+ -> ( ( x ^ 2 ) e. CC /\ ( x ^ 2 ) =/= 0 ) )
114	47, 113	syl 17	. . . . . . . . . . 11 |- ( ( ( ph /\ x e. RR+ ) /\ n e. ( ZZ>= ` ( ( |_ ` ( 4 / ( x ^ 2 ) ) ) + 1 ) ) ) -> ( ( x ^ 2 ) e. CC /\ ( x ^ 2 ) =/= 0 ) )
115		rpcnne0 11850	. . . . . . . . . . . 12 |- ( 4 e. RR+ -> ( 4 e. CC /\ 4 =/= 0 ) )
116	3, 115	ax-mp 5	. . . . . . . . . . 11 |- ( 4 e. CC /\ 4 =/= 0 )
117		recdiv 10731	. . . . . . . . . . 11 |- ( ( ( ( x ^ 2 ) e. CC /\ ( x ^ 2 ) =/= 0 ) /\ ( 4 e. CC /\ 4 =/= 0 ) ) -> ( 1 / ( ( x ^ 2 ) / 4 ) ) = ( 4 / ( x ^ 2 ) ) )
118	114, 116, 117	sylancl 694	. . . . . . . . . 10 |- ( ( ( ph /\ x e. RR+ ) /\ n e. ( ZZ>= ` ( ( |_ ` ( 4 / ( x ^ 2 ) ) ) + 1 ) ) ) -> ( 1 / ( ( x ^ 2 ) / 4 ) ) = ( 4 / ( x ^ 2 ) ) )
119	9	adantr 481	. . . . . . . . . . . 12 |- ( ( ( ph /\ x e. RR+ ) /\ n e. ( ZZ>= ` ( ( |_ ` ( 4 / ( x ^ 2 ) ) ) + 1 ) ) ) -> ( 4 / ( x ^ 2 ) ) e. RR+ )
120	119	rpred 11872	. . . . . . . . . . 11 |- ( ( ( ph /\ x e. RR+ ) /\ n e. ( ZZ>= ` ( ( |_ ` ( 4 / ( x ^ 2 ) ) ) + 1 ) ) ) -> ( 4 / ( x ^ 2 ) ) e. RR )
121		flltp1 12601	. . . . . . . . . . 11 |- ( ( 4 / ( x ^ 2 ) ) e. RR -> ( 4 / ( x ^ 2 ) ) < ( ( |_ ` ( 4 / ( x ^ 2 ) ) ) + 1 ) )
122	120, 121	syl 17	. . . . . . . . . 10 |- ( ( ( ph /\ x e. RR+ ) /\ n e. ( ZZ>= ` ( ( |_ ` ( 4 / ( x ^ 2 ) ) ) + 1 ) ) ) -> ( 4 / ( x ^ 2 ) ) < ( ( |_ ` ( 4 / ( x ^ 2 ) ) ) + 1 ) )
123	118, 122	eqbrtrd 4675	. . . . . . . . 9 |- ( ( ( ph /\ x e. RR+ ) /\ n e. ( ZZ>= ` ( ( |_ ` ( 4 / ( x ^ 2 ) ) ) + 1 ) ) ) -> ( 1 / ( ( x ^ 2 ) / 4 ) ) < ( ( |_ ` ( 4 / ( x ^ 2 ) ) ) + 1 ) )
124	112, 42, 123	ltrec1d 11892	. . . . . . . 8 |- ( ( ( ph /\ x e. RR+ ) /\ n e. ( ZZ>= ` ( ( |_ ` ( 4 / ( x ^ 2 ) ) ) + 1 ) ) ) -> ( 1 / ( ( |_ ` ( 4 / ( x ^ 2 ) ) ) + 1 ) ) < ( ( x ^ 2 ) / 4 ) )
125	1, 2	pm3.2i 471	. . . . . . . . . 10 |- ( 4 e. RR /\ 0 < 4 )
126		ltmuldiv2 10897	. . . . . . . . . 10 |- ( ( ( 1 / ( ( |_ ` ( 4 / ( x ^ 2 ) ) ) + 1 ) ) e. RR /\ ( x ^ 2 ) e. RR /\ ( 4 e. RR /\ 0 < 4 ) ) -> ( ( 4 x. ( 1 / ( ( |_ ` ( 4 / ( x ^ 2 ) ) ) + 1 ) ) ) < ( x ^ 2 ) <-> ( 1 / ( ( |_ ` ( 4 / ( x ^ 2 ) ) ) + 1 ) ) < ( ( x ^ 2 ) / 4 ) ) )
127	125, 126	mp3an3 1413	. . . . . . . . 9 |- ( ( ( 1 / ( ( |_ ` ( 4 / ( x ^ 2 ) ) ) + 1 ) ) e. RR /\ ( x ^ 2 ) e. RR ) -> ( ( 4 x. ( 1 / ( ( |_ ` ( 4 / ( x ^ 2 ) ) ) + 1 ) ) ) < ( x ^ 2 ) <-> ( 1 / ( ( |_ ` ( 4 / ( x ^ 2 ) ) ) + 1 ) ) < ( ( x ^ 2 ) / 4 ) ) )
128	61, 48, 127	syl2anc 693	. . . . . . . 8 |- ( ( ( ph /\ x e. RR+ ) /\ n e. ( ZZ>= ` ( ( |_ ` ( 4 / ( x ^ 2 ) ) ) + 1 ) ) ) -> ( ( 4 x. ( 1 / ( ( |_ ` ( 4 / ( x ^ 2 ) ) ) + 1 ) ) ) < ( x ^ 2 ) <-> ( 1 / ( ( |_ ` ( 4 / ( x ^ 2 ) ) ) + 1 ) ) < ( ( x ^ 2 ) / 4 ) ) )
129	124, 128	mpbird 247	. . . . . . 7 |- ( ( ( ph /\ x e. RR+ ) /\ n e. ( ZZ>= ` ( ( |_ ` ( 4 / ( x ^ 2 ) ) ) + 1 ) ) ) -> ( 4 x. ( 1 / ( ( |_ ` ( 4 / ( x ^ 2 ) ) ) + 1 ) ) ) < ( x ^ 2 ) )
130	41, 46, 48, 110, 129	lelttrd 10195	. . . . . 6 |- ( ( ( ph /\ x e. RR+ ) /\ n e. ( ZZ>= ` ( ( |_ ` ( 4 / ( x ^ 2 ) ) ) + 1 ) ) ) -> ( ( ( F ` ( ( |_ ` ( 4 / ( x ^ 2 ) ) ) + 1 ) ) D ( F ` n ) ) ^ 2 ) < ( x ^ 2 ) )
131		metge0 22150	. . . . . . . 8 |- ( ( D e. ( Met ` X ) /\ ( F ` ( ( |_ ` ( 4 / ( x ^ 2 ) ) ) + 1 ) ) e. X /\ ( F ` n ) e. X ) -> 0 <_ ( ( F ` ( ( |_ ` ( 4 / ( x ^ 2 ) ) ) + 1 ) ) D ( F ` n ) ) )
132	20, 34, 38, 131	syl3anc 1326	. . . . . . 7 |- ( ( ( ph /\ x e. RR+ ) /\ n e. ( ZZ>= ` ( ( |_ ` ( 4 / ( x ^ 2 ) ) ) + 1 ) ) ) -> 0 <_ ( ( F ` ( ( |_ ` ( 4 / ( x ^ 2 ) ) ) + 1 ) ) D ( F ` n ) ) )
133		rprege0 11847	. . . . . . . 8 |- ( x e. RR+ -> ( x e. RR /\ 0 <_ x ) )
134	133	ad2antlr 763	. . . . . . 7 |- ( ( ( ph /\ x e. RR+ ) /\ n e. ( ZZ>= ` ( ( |_ ` ( 4 / ( x ^ 2 ) ) ) + 1 ) ) ) -> ( x e. RR /\ 0 <_ x ) )
135		lt2sq 12937	. . . . . . 7 |- ( ( ( ( ( F ` ( ( |_ ` ( 4 / ( x ^ 2 ) ) ) + 1 ) ) D ( F ` n ) ) e. RR /\ 0 <_ ( ( F ` ( ( |_ ` ( 4 / ( x ^ 2 ) ) ) + 1 ) ) D ( F ` n ) ) ) /\ ( x e. RR /\ 0 <_ x ) ) -> ( ( ( F ` ( ( |_ ` ( 4 / ( x ^ 2 ) ) ) + 1 ) ) D ( F ` n ) ) < x <-> ( ( ( F ` ( ( |_ ` ( 4 / ( x ^ 2 ) ) ) + 1 ) ) D ( F ` n ) ) ^ 2 ) < ( x ^ 2 ) ) )
136	40, 132, 134, 135	syl21anc 1325	. . . . . 6 |- ( ( ( ph /\ x e. RR+ ) /\ n e. ( ZZ>= ` ( ( |_ ` ( 4 / ( x ^ 2 ) ) ) + 1 ) ) ) -> ( ( ( F ` ( ( |_ ` ( 4 / ( x ^ 2 ) ) ) + 1 ) ) D ( F ` n ) ) < x <-> ( ( ( F ` ( ( |_ ` ( 4 / ( x ^ 2 ) ) ) + 1 ) ) D ( F ` n ) ) ^ 2 ) < ( x ^ 2 ) ) )
137	130, 136	mpbird 247	. . . . 5 |- ( ( ( ph /\ x e. RR+ ) /\ n e. ( ZZ>= ` ( ( |_ ` ( 4 / ( x ^ 2 ) ) ) + 1 ) ) ) -> ( ( F ` ( ( |_ ` ( 4 / ( x ^ 2 ) ) ) + 1 ) ) D ( F ` n ) ) < x )
138	137	ralrimiva 2966	. . . 4 |- ( ( ph /\ x e. RR+ ) -> A. n e. ( ZZ>= ` ( ( |_ ` ( 4 / ( x ^ 2 ) ) ) + 1 ) ) ( ( F ` ( ( |_ ` ( 4 / ( x ^ 2 ) ) ) + 1 ) ) D ( F ` n ) ) < x )
139		fveq2 6191	. . . . . 6 |- ( j = ( ( |_ ` ( 4 / ( x ^ 2 ) ) ) + 1 ) -> ( ZZ>= ` j ) = ( ZZ>= ` ( ( |_ ` ( 4 / ( x ^ 2 ) ) ) + 1 ) ) )
140		fveq2 6191	. . . . . . . 8 |- ( j = ( ( |_ ` ( 4 / ( x ^ 2 ) ) ) + 1 ) -> ( F ` j ) = ( F ` ( ( |_ ` ( 4 / ( x ^ 2 ) ) ) + 1 ) ) )
141	140	oveq1d 6665	. . . . . . 7 |- ( j = ( ( |_ ` ( 4 / ( x ^ 2 ) ) ) + 1 ) -> ( ( F ` j ) D ( F ` n ) ) = ( ( F ` ( ( |_ ` ( 4 / ( x ^ 2 ) ) ) + 1 ) ) D ( F ` n ) ) )
142	141	breq1d 4663	. . . . . 6 |- ( j = ( ( |_ ` ( 4 / ( x ^ 2 ) ) ) + 1 ) -> ( ( ( F ` j ) D ( F ` n ) ) < x <-> ( ( F ` ( ( |_ ` ( 4 / ( x ^ 2 ) ) ) + 1 ) ) D ( F ` n ) ) < x ) )
143	139, 142	raleqbidv 3152	. . . . 5 |- ( j = ( ( |_ ` ( 4 / ( x ^ 2 ) ) ) + 1 ) -> ( A. n e. ( ZZ>= ` j ) ( ( F ` j ) D ( F ` n ) ) < x <-> A. n e. ( ZZ>= ` ( ( |_ ` ( 4 / ( x ^ 2 ) ) ) + 1 ) ) ( ( F ` ( ( |_ ` ( 4 / ( x ^ 2 ) ) ) + 1 ) ) D ( F ` n ) ) < x ) )
144	143	rspcev 3309	. . . 4 |- ( ( ( ( |_ ` ( 4 / ( x ^ 2 ) ) ) + 1 ) e. NN /\ A. n e. ( ZZ>= ` ( ( |_ ` ( 4 / ( x ^ 2 ) ) ) + 1 ) ) ( ( F ` ( ( |_ ` ( 4 / ( x ^ 2 ) ) ) + 1 ) ) D ( F ` n ) ) < x ) -> E. j e. NN A. n e. ( ZZ>= ` j ) ( ( F ` j ) D ( F ` n ) ) < x )
145	13, 138, 144	syl2anc 693	. . 3 |- ( ( ph /\ x e. RR+ ) -> E. j e. NN A. n e. ( ZZ>= ` j ) ( ( F ` j ) D ( F ` n ) ) < x )
146	145	ralrimiva 2966	. 2 |- ( ph -> A. x e. RR+ E. j e. NN A. n e. ( ZZ>= ` j ) ( ( F ` j ) D ( F ` n ) ) < x )
147		nnuz 11723	. . 3 |- NN = ( ZZ>= ` 1 )
148	16, 17	imsxmet 27547	. . . 4 |- ( U e. NrmCVec -> D e. ( *Met ` X ) )
149	14, 15, 148	3syl 18	. . 3 |- ( ph -> D e. ( *Met ` X ) )
150		1zzd 11408	. . 3 |- ( ph -> 1 e. ZZ )
151		eqidd 2623	. . 3 |- ( ( ph /\ n e. NN ) -> ( F ` n ) = ( F ` n ) )
152		eqidd 2623	. . 3 |- ( ( ph /\ j e. NN ) -> ( F ` j ) = ( F ` j ) )
153	30, 28	fssd 6057	. . 3 |- ( ph -> F : NN --> X )
154	147, 149, 150, 151, 152, 153	iscauf 23078	. 2 |- ( ph -> ( F e. ( Cau ` D ) <-> A. x e. RR+ E. j e. NN A. n e. ( ZZ>= ` j ) ( ( F ` j ) D ( F ` n ) ) < x ) )
155	146, 154	mpbird 247	1 |- ( ph -> F e. ( Cau ` D ) )

Syntax hints:   -> wi 4   <-> wb 196   /\ wa 384   /\ w3a 1037   = wceq 1483   e. wcel 1990   =/= wne 2794   A.wral 2912   E.wrex 2913   i^i cin 3573   C_ wss 3574   (/)c0 3915   class class class wbr 4653   |-> cmpt 4729   ran crn 5115   -->wf 5884   ` cfv 5888  (class class class)co 6650  infcinf 8347   CCcc 9934   RRcr 9935   0cc0 9936   1c1 9937   + caddc 9939   x. cmul 9941   < clt 10074   <_ cle 10075   / cdiv 10684   NNcn 11020   2c2 11070   4c4 11072   NN0cn0 11292   ZZcz 11377   ZZ>=cuz 11687   RR+crp 11832   |_cfl 12591   ^cexp 12860   *Metcxmt 19731   Metcme 19732   MetOpencmopn 19736   Caucca 23051   NrmCVeccnv 27439   BaseSetcba 27441   -vcnsb 27444   norm_CVcnmcv 27445   IndMetcims 27446   SubSpcss 27576   CPreHil OLDccphlo 27667   CBanccbn 27718

This theorem was proved from axioms:  ax-mp 5  ax-1 6  ax-2 7  ax-3 8  ax-gen 1722  ax-4 1737  ax-5 1839  ax-6 1888  ax-7 1935  ax-8 1992  ax-9 1999  ax-10 2019  ax-11 2034  ax-12 2047  ax-13 2246  ax-ext 2602  ax-rep 4771  ax-sep 4781  ax-nul 4789  ax-pow 4843  ax-pr 4906  ax-un 6949  ax-cnex 9992  ax-resscn 9993  ax-1cn 9994  ax-icn 9995  ax-addcl 9996  ax-addrcl 9997  ax-mulcl 9998  ax-mulrcl 9999  ax-mulcom 10000  ax-addass 10001  ax-mulass 10002  ax-distr 10003  ax-i2m1 10004  ax-1ne0 10005  ax-1rid 10006  ax-rnegex 10007  ax-rrecex 10008  ax-cnre 10009  ax-pre-lttri 10010  ax-pre-lttrn 10011  ax-pre-ltadd 10012  ax-pre-mulgt0 10013  ax-pre-sup 10014  ax-addf 10015  ax-mulf 10016

This theorem depends on definitions:  df-bi 197  df-or 385  df-an 386  df-3or 1038  df-3an 1039  df-tru 1486  df-ex 1705  df-nf 1710  df-sb 1881  df-eu 2474  df-mo 2475  df-clab 2609  df-cleq 2615  df-clel 2618  df-nfc 2753  df-ne 2795  df-nel 2898  df-ral 2917  df-rex 2918  df-reu 2919  df-rmo 2920  df-rab 2921  df-v 3202  df-sbc 3436  df-csb 3534  df-dif 3577  df-un 3579  df-in 3581  df-ss 3588  df-pss 3590  df-nul 3916  df-if 4087  df-pw 4160  df-sn 4178  df-pr 4180  df-tp 4182  df-op 4184  df-uni 4437  df-iun 4522  df-br 4654  df-opab 4713  df-mpt 4730  df-tr 4753  df-id 5024  df-eprel 5029  df-po 5035  df-so 5036  df-fr 5073  df-we 5075  df-xp 5120  df-rel 5121  df-cnv 5122  df-co 5123  df-dm 5124  df-rn 5125  df-res 5126  df-ima 5127  df-pred 5680  df-ord 5726  df-on 5727  df-lim 5728  df-suc 5729  df-iota 5851  df-fun 5890  df-fn 5891  df-f 5892  df-f1 5893  df-fo 5894  df-f1o 5895  df-fv 5896  df-riota 6611  df-ov 6653  df-oprab 6654  df-mpt2 6655  df-om 7066  df-1st 7168  df-2nd 7169  df-wrecs 7407  df-recs 7468  df-rdg 7506  df-er 7742  df-map 7859  df-pm 7860  df-en 7956  df-dom 7957  df-sdom 7958  df-sup 8348  df-inf 8349  df-pnf 10076  df-mnf 10077  df-xr 10078  df-ltxr 10079  df-le 10080  df-sub 10268  df-neg 10269  df-div 10685  df-nn 11021  df-2 11079  df-3 11080  df-4 11081  df-n0 11293  df-z 11378  df-uz 11688  df-rp 11833  df-xneg 11946  df-xadd 11947  df-xmul 11948  df-fl 12593  df-seq 12802  df-exp 12861  df-cj 13839  df-re 13840  df-im 13841  df-sqrt 13975  df-abs 13976  df-psmet 19738  df-xmet 19739  df-met 19740  df-bl 19741  df-cau 23054  df-grpo 27347  df-gid 27348  df-ginv 27349  df-gdiv 27350  df-ablo 27399  df-vc 27414  df-nv 27447  df-va 27450  df-ba 27451  df-sm 27452  df-0v 27453  df-vs 27454  df-nmcv 27455  df-ims 27456  df-ssp 27577  df-ph 27668  df-cbn 27719

This theorem is referenced by:  minvecolem4a  27733