| Description: The other half of rpnnen 14956, where we show an injection from sets of
positive integers to real numbers. The obvious choice for this is
binary expansion, but it has the unfortunate property that it does not
produce an injection on numbers which end with all 0's or all 1's (the
more well-known decimal version of this is 0.999... 14612). Instead, we
opt for a ternary expansion, which produces (a scaled version of) the
Cantor set. Since the Cantor set is riddled with gaps, we can show that
any two sequences that are not equal must differ somewhere, and when
they do, they are placed a finite distance apart, thus ensuring that the
map is injective.
Our map assigns to each subset  of the positive integers the number of the positive integers the number
     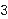 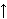                  , where , where
                 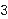 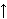        (rpnnen2lem1 14943). This is an infinite sum of real numbers
(rpnnen2lem2 14944), and since
(rpnnen2lem1 14943). This is an infinite sum of real numbers
(rpnnen2lem2 14944), and since    implies
implies
     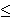      (rpnnen2lem4 14946) and (rpnnen2lem4 14946) and      converges to
converges to    (rpnnen2lem3 14945) by geoisum1 14610, the sum is
convergent to some real (rpnnen2lem5 14947 and rpnnen2lem6 14948) by the
comparison test for convergence cvgcmp 14548. The comparison test also
tells us that (rpnnen2lem3 14945) by geoisum1 14610, the sum is
convergent to some real (rpnnen2lem5 14947 and rpnnen2lem6 14948) by the
comparison test for convergence cvgcmp 14548. The comparison test also
tells us that 
  implies implies       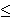       (rpnnen2lem7 14949).
(rpnnen2lem7 14949).
Putting it all together, if we have two sets    , there
must
differ somewhere, and so there must be an , there
must
differ somewhere, and so there must be an  such that such that
         
   but but        or vice versa.
In this case, we split off the first or vice versa.
In this case, we split off the first    terms (rpnnen2lem8 14950)
and cancel them (rpnnen2lem10 14952), since these are the same for both
sets. For the remaining terms, we use the subset property to establish
that terms (rpnnen2lem8 14950)
and cancel them (rpnnen2lem10 14952), since these are the same for both
sets. For the remaining terms, we use the subset property to establish
that       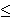             and and
        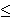
      (where these sums are only
over (where these sums are only
over  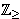    ), and since ), and since
              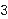 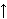      (rpnnen2lem9 14951)
and (rpnnen2lem9 14951)
and           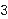 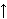    , we establish that , we establish that
             (rpnnen2lem11 14953) so that they
must be different. By contraposition (rpnnen2lem12 14954), we find that
this map is an injection. (Contributed by Mario Carneiro, 13-May-2013.)
(Proof shortened by Mario Carneiro, 30-Apr-2014.) (Revised by NM,
17-Aug-2021.) (rpnnen2lem11 14953) so that they
must be different. By contraposition (rpnnen2lem12 14954), we find that
this map is an injection. (Contributed by Mario Carneiro, 13-May-2013.)
(Proof shortened by Mario Carneiro, 30-Apr-2014.) (Revised by NM,
17-Aug-2021.) |