Users' Mathboxes Mathbox for Mario Carneiro < Previous   Next >
Nearby theorems
Mirrors  >  Home  >  MPE Home  >  Th. List  >   Mathboxes  >  connpconn Structured version   Visualization version   Unicode version
Theorem connpconn 31217
Description: A connected and locally path-connected space is path-connected. (Contributed by Mario Carneiro, 7-Jul-2015.)
Assertion
Ref Expression
connpconn |- ( ( J e. Conn /\ J e. 𝑛Locally PConn ) -> J e. PConn )
Proof of Theorem connpconn
Dummy variables x f y z g h s u w are mutually distinct and distinct from all other variables.
StepHypRef Expression
1 conntop 21220 . . 3 |- ( J e. Conn -> J e. Top )
21adantr 481 . 2 |- ( ( J e. Conn /\ J e. 𝑛Locally PConn ) -> J e. Top )
3 eqid 2622 . . . . . 6 |- U. J = U. J
4 simpll 790 . . . . . 6 |- ( ( ( J e. Conn /\ J e. 𝑛Locally PConn ) /\ x e. U. J ) -> J e. Conn )
5 inss1 3833 . . . . . . 7 |- ( J i^i ( Clsd ` J ) ) C_ J
6 simplr 792 . . . . . . . . . . . 12 |- ( ( ( J e. Conn /\ J e. 𝑛Locally PConn ) /\ ( x e. U. J /\ z e. U. J ) ) -> J e. 𝑛Locally PConn )
71ad2antrr 762 . . . . . . . . . . . . 13 |- ( ( ( J e. Conn /\ J e. 𝑛Locally PConn ) /\ ( x e. U. J /\ z e. U. J ) ) -> J e. Top )
83topopn 20711 . . . . . . . . . . . . 13 |- ( J e. Top -> U. J e. J )
97, 8syl 17 . . . . . . . . . . . 12 |- ( ( ( J e. Conn /\ J e. 𝑛Locally PConn ) /\ ( x e. U. J /\ z e. U. J ) ) -> U. J e. J )
10 simprr 796 . . . . . . . . . . . 12 |- ( ( ( J e. Conn /\ J e. 𝑛Locally PConn ) /\ ( x e. U. J /\ z e. U. J ) ) -> z e. U. J )
11 nlly2i 21279 . . . . . . . . . . . 12 |- ( ( J e. 𝑛Locally PConn /\ U. J e. J /\ z e. U. J ) -> E. s e. ~P U. J E. u e. J ( z e. u /\ u C_ s /\ ( J ↾t s ) e. PConn ) )
126, 9, 10, 11syl3anc 1326 . . . . . . . . . . 11 |- ( ( ( J e. Conn /\ J e. 𝑛Locally PConn ) /\ ( x e. U. J /\ z e. U. J ) ) -> E. s e. ~P U. J E. u e. J ( z e. u /\ u C_ s /\ ( J ↾t s ) e. PConn ) )
13 simprr1 1109 . . . . . . . . . . . . . . 15 |- ( ( ( ( J e. Conn /\ J e. 𝑛Locally PConn ) /\ ( x e. U. J /\ z e. U. J ) ) /\ ( s e. ~P U. J /\ ( z e. u /\ u C_ s /\ ( J ↾t s ) e. PConn ) ) ) -> z e. u )
14 eqeq2 2633 . . . . . . . . . . . . . . . . . . . . 21 |- ( y = w -> ( ( f ` 1 ) = y <-> ( f ` 1 ) = w ) )
1514anbi2d 740 . . . . . . . . . . . . . . . . . . . 20 |- ( y = w -> ( ( ( f ` 0 ) = x /\ ( f ` 1 ) = y ) <-> ( ( f ` 0 ) = x /\ ( f ` 1 ) = w ) ) )
1615rexbidv 3052 . . . . . . . . . . . . . . . . . . 19 |- ( y = w -> ( E. f e. ( II Cn J ) ( ( f ` 0 ) = x /\ ( f ` 1 ) = y ) <-> E. f e. ( II Cn J ) ( ( f ` 0 ) = x /\ ( f ` 1 ) = w ) ) )
1716elrab 3363 . . . . . . . . . . . . . . . . . 18 |- ( w e. { y e. U. J | E. f e. ( II Cn J ) ( ( f ` 0 ) = x /\ ( f ` 1 ) = y ) } <-> ( w e. U. J /\ E. f e. ( II Cn J ) ( ( f ` 0 ) = x /\ ( f ` 1 ) = w ) ) )
1817simprbi 480 . . . . . . . . . . . . . . . . 17 |- ( w e. { y e. U. J | E. f e. ( II Cn J ) ( ( f ` 0 ) = x /\ ( f ` 1 ) = y ) } -> E. f e. ( II Cn J ) ( ( f ` 0 ) = x /\ ( f ` 1 ) = w ) )
19 simprr3 1111 . . . . . . . . . . . . . . . . . . . . . . . . . 26 |- ( ( ( ( J e. Conn /\ J e. 𝑛Locally PConn ) /\ ( x e. U. J /\ z e. U. J ) ) /\ ( s e. ~P U. J /\ ( z e. u /\ u C_ s /\ ( J ↾t s ) e. PConn ) ) ) -> ( J ↾t s ) e. PConn )
2019adantr 481 . . . . . . . . . . . . . . . . . . . . . . . . 25 |- ( ( ( ( ( J e. Conn /\ J e. 𝑛Locally PConn ) /\ ( x e. U. J /\ z e. U. J ) ) /\ ( s e. ~P U. J /\ ( z e. u /\ u C_ s /\ ( J ↾t s ) e. PConn ) ) ) /\ ( ( w e. u /\ ( g e. ( II Cn J ) /\ ( ( g ` 0 ) = x /\ ( g ` 1 ) = w ) ) ) /\ y e. u ) ) -> ( J ↾t s ) e. PConn )
21 simprr2 1110 . . . . . . . . . . . . . . . . . . . . . . . . . . . 28 |- ( ( ( ( J e. Conn /\ J e. 𝑛Locally PConn ) /\ ( x e. U. J /\ z e. U. J ) ) /\ ( s e. ~P U. J /\ ( z e. u /\ u C_ s /\ ( J ↾t s ) e. PConn ) ) ) -> u C_ s )
2221adantr 481 . . . . . . . . . . . . . . . . . . . . . . . . . . 27 |- ( ( ( ( ( J e. Conn /\ J e. 𝑛Locally PConn ) /\ ( x e. U. J /\ z e. U. J ) ) /\ ( s e. ~P U. J /\ ( z e. u /\ u C_ s /\ ( J ↾t s ) e. PConn ) ) ) /\ ( ( w e. u /\ ( g e. ( II Cn J ) /\ ( ( g ` 0 ) = x /\ ( g ` 1 ) = w ) ) ) /\ y e. u ) ) -> u C_ s )
23 simprll 802 . . . . . . . . . . . . . . . . . . . . . . . . . . 27 |- ( ( ( ( ( J e. Conn /\ J e. 𝑛Locally PConn ) /\ ( x e. U. J /\ z e. U. J ) ) /\ ( s e. ~P U. J /\ ( z e. u /\ u C_ s /\ ( J ↾t s ) e. PConn ) ) ) /\ ( ( w e. u /\ ( g e. ( II Cn J ) /\ ( ( g ` 0 ) = x /\ ( g ` 1 ) = w ) ) ) /\ y e. u ) ) -> w e. u )
2422, 23sseldd 3604 . . . . . . . . . . . . . . . . . . . . . . . . . 26 |- ( ( ( ( ( J e. Conn /\ J e. 𝑛Locally PConn ) /\ ( x e. U. J /\ z e. U. J ) ) /\ ( s e. ~P U. J /\ ( z e. u /\ u C_ s /\ ( J ↾t s ) e. PConn ) ) ) /\ ( ( w e. u /\ ( g e. ( II Cn J ) /\ ( ( g ` 0 ) = x /\ ( g ` 1 ) = w ) ) ) /\ y e. u ) ) -> w e. s )
257ad2antrr 762 . . . . . . . . . . . . . . . . . . . . . . . . . . 27 |- ( ( ( ( ( J e. Conn /\ J e. 𝑛Locally PConn ) /\ ( x e. U. J /\ z e. U. J ) ) /\ ( s e. ~P U. J /\ ( z e. u /\ u C_ s /\ ( J ↾t s ) e. PConn ) ) ) /\ ( ( w e. u /\ ( g e. ( II Cn J ) /\ ( ( g ` 0 ) = x /\ ( g ` 1 ) = w ) ) ) /\ y e. u ) ) -> J e. Top )
26 elpwi 4168 . . . . . . . . . . . . . . . . . . . . . . . . . . . . 29 |- ( s e. ~P U. J -> s C_ U. J )
2726ad2antrl 764 . . . . . . . . . . . . . . . . . . . . . . . . . . . 28 |- ( ( ( ( J e. Conn /\ J e. 𝑛Locally PConn ) /\ ( x e. U. J /\ z e. U. J ) ) /\ ( s e. ~P U. J /\ ( z e. u /\ u C_ s /\ ( J ↾t s ) e. PConn ) ) ) -> s C_ U. J )
2827adantr 481 . . . . . . . . . . . . . . . . . . . . . . . . . . 27 |- ( ( ( ( ( J e. Conn /\ J e. 𝑛Locally PConn ) /\ ( x e. U. J /\ z e. U. J ) ) /\ ( s e. ~P U. J /\ ( z e. u /\ u C_ s /\ ( J ↾t s ) e. PConn ) ) ) /\ ( ( w e. u /\ ( g e. ( II Cn J ) /\ ( ( g ` 0 ) = x /\ ( g ` 1 ) = w ) ) ) /\ y e. u ) ) -> s C_ U. J )
293restuni 20966 . . . . . . . . . . . . . . . . . . . . . . . . . . 27 |- ( ( J e. Top /\ s C_ U. J ) -> s = U. ( J ↾t s ) )
3025, 28, 29syl2anc 693 . . . . . . . . . . . . . . . . . . . . . . . . . 26 |- ( ( ( ( ( J e. Conn /\ J e. 𝑛Locally PConn ) /\ ( x e. U. J /\ z e. U. J ) ) /\ ( s e. ~P U. J /\ ( z e. u /\ u C_ s /\ ( J ↾t s ) e. PConn ) ) ) /\ ( ( w e. u /\ ( g e. ( II Cn J ) /\ ( ( g ` 0 ) = x /\ ( g ` 1 ) = w ) ) ) /\ y e. u ) ) -> s = U. ( J ↾t s ) )
3124, 30eleqtrd 2703 . . . . . . . . . . . . . . . . . . . . . . . . 25 |- ( ( ( ( ( J e. Conn /\ J e. 𝑛Locally PConn ) /\ ( x e. U. J /\ z e. U. J ) ) /\ ( s e. ~P U. J /\ ( z e. u /\ u C_ s /\ ( J ↾t s ) e. PConn ) ) ) /\ ( ( w e. u /\ ( g e. ( II Cn J ) /\ ( ( g ` 0 ) = x /\ ( g ` 1 ) = w ) ) ) /\ y e. u ) ) -> w e. U. ( J ↾t s ) )
32 simprr 796 . . . . . . . . . . . . . . . . . . . . . . . . . . 27 |- ( ( ( ( ( J e. Conn /\ J e. 𝑛Locally PConn ) /\ ( x e. U. J /\ z e. U. J ) ) /\ ( s e. ~P U. J /\ ( z e. u /\ u C_ s /\ ( J ↾t s ) e. PConn ) ) ) /\ ( ( w e. u /\ ( g e. ( II Cn J ) /\ ( ( g ` 0 ) = x /\ ( g ` 1 ) = w ) ) ) /\ y e. u ) ) -> y e. u )
3322, 32sseldd 3604 . . . . . . . . . . . . . . . . . . . . . . . . . 26 |- ( ( ( ( ( J e. Conn /\ J e. 𝑛Locally PConn ) /\ ( x e. U. J /\ z e. U. J ) ) /\ ( s e. ~P U. J /\ ( z e. u /\ u C_ s /\ ( J ↾t s ) e. PConn ) ) ) /\ ( ( w e. u /\ ( g e. ( II Cn J ) /\ ( ( g ` 0 ) = x /\ ( g ` 1 ) = w ) ) ) /\ y e. u ) ) -> y e. s )
3433, 30eleqtrd 2703 . . . . . . . . . . . . . . . . . . . . . . . . 25 |- ( ( ( ( ( J e. Conn /\ J e. 𝑛Locally PConn ) /\ ( x e. U. J /\ z e. U. J ) ) /\ ( s e. ~P U. J /\ ( z e. u /\ u C_ s /\ ( J ↾t s ) e. PConn ) ) ) /\ ( ( w e. u /\ ( g e. ( II Cn J ) /\ ( ( g ` 0 ) = x /\ ( g ` 1 ) = w ) ) ) /\ y e. u ) ) -> y e. U. ( J ↾t s ) )
35 eqid 2622 . . . . . . . . . . . . . . . . . . . . . . . . . 26 |- U. ( J ↾t s ) = U. ( J ↾t s )
3635pconncn 31206 . . . . . . . . . . . . . . . . . . . . . . . . 25 |- ( ( ( J ↾t s ) e. PConn /\ w e. U. ( J ↾t s ) /\ y e. U. ( J ↾t s ) ) -> E. h e. ( II Cn ( J ↾t s ) ) ( ( h ` 0 ) = w /\ ( h ` 1 ) = y ) )
3720, 31, 34, 36syl3anc 1326 . . . . . . . . . . . . . . . . . . . . . . . 24 |- ( ( ( ( ( J e. Conn /\ J e. 𝑛Locally PConn ) /\ ( x e. U. J /\ z e. U. J ) ) /\ ( s e. ~P U. J /\ ( z e. u /\ u C_ s /\ ( J ↾t s ) e. PConn ) ) ) /\ ( ( w e. u /\ ( g e. ( II Cn J ) /\ ( ( g ` 0 ) = x /\ ( g ` 1 ) = w ) ) ) /\ y e. u ) ) -> E. h e. ( II Cn ( J ↾t s ) ) ( ( h ` 0 ) = w /\ ( h ` 1 ) = y ) )
38 simplrl 800 . . . . . . . . . . . . . . . . . . . . . . . . . . 27 |- ( ( ( w e. u /\ ( g e. ( II Cn J ) /\ ( ( g ` 0 ) = x /\ ( g ` 1 ) = w ) ) ) /\ y e. u ) -> g e. ( II Cn J ) )
3938ad2antlr 763 . . . . . . . . . . . . . . . . . . . . . . . . . 26 |- ( ( ( ( ( ( J e. Conn /\ J e. 𝑛Locally PConn ) /\ ( x e. U. J /\ z e. U. J ) ) /\ ( s e. ~P U. J /\ ( z e. u /\ u C_ s /\ ( J ↾t s ) e. PConn ) ) ) /\ ( ( w e. u /\ ( g e. ( II Cn J ) /\ ( ( g ` 0 ) = x /\ ( g ` 1 ) = w ) ) ) /\ y e. u ) ) /\ ( h e. ( II Cn ( J ↾t s ) ) /\ ( ( h ` 0 ) = w /\ ( h ` 1 ) = y ) ) ) -> g e. ( II Cn J ) )
4025adantr 481 . . . . . . . . . . . . . . . . . . . . . . . . . . . 28 |- ( ( ( ( ( ( J e. Conn /\ J e. 𝑛Locally PConn ) /\ ( x e. U. J /\ z e. U. J ) ) /\ ( s e. ~P U. J /\ ( z e. u /\ u C_ s /\ ( J ↾t s ) e. PConn ) ) ) /\ ( ( w e. u /\ ( g e. ( II Cn J ) /\ ( ( g ` 0 ) = x /\ ( g ` 1 ) = w ) ) ) /\ y e. u ) ) /\ ( h e. ( II Cn ( J ↾t s ) ) /\ ( ( h ` 0 ) = w /\ ( h ` 1 ) = y ) ) ) -> J e. Top )
41 cnrest2r 21091 . . . . . . . . . . . . . . . . . . . . . . . . . . . 28 |- ( J e. Top -> ( II Cn ( J ↾t s ) ) C_ ( II Cn J ) )
4240, 41syl 17 . . . . . . . . . . . . . . . . . . . . . . . . . . 27 |- ( ( ( ( ( ( J e. Conn /\ J e. 𝑛Locally PConn ) /\ ( x e. U. J /\ z e. U. J ) ) /\ ( s e. ~P U. J /\ ( z e. u /\ u C_ s /\ ( J ↾t s ) e. PConn ) ) ) /\ ( ( w e. u /\ ( g e. ( II Cn J ) /\ ( ( g ` 0 ) = x /\ ( g ` 1 ) = w ) ) ) /\ y e. u ) ) /\ ( h e. ( II Cn ( J ↾t s ) ) /\ ( ( h ` 0 ) = w /\ ( h ` 1 ) = y ) ) ) -> ( II Cn ( J ↾t s ) ) C_ ( II Cn J ) )
43 simprl 794 . . . . . . . . . . . . . . . . . . . . . . . . . . 27 |- ( ( ( ( ( ( J e. Conn /\ J e. 𝑛Locally PConn ) /\ ( x e. U. J /\ z e. U. J ) ) /\ ( s e. ~P U. J /\ ( z e. u /\ u C_ s /\ ( J ↾t s ) e. PConn ) ) ) /\ ( ( w e. u /\ ( g e. ( II Cn J ) /\ ( ( g ` 0 ) = x /\ ( g ` 1 ) = w ) ) ) /\ y e. u ) ) /\ ( h e. ( II Cn ( J ↾t s ) ) /\ ( ( h ` 0 ) = w /\ ( h ` 1 ) = y ) ) ) -> h e. ( II Cn ( J ↾t s ) ) )
4442, 43sseldd 3604 . . . . . . . . . . . . . . . . . . . . . . . . . 26 |- ( ( ( ( ( ( J e. Conn /\ J e. 𝑛Locally PConn ) /\ ( x e. U. J /\ z e. U. J ) ) /\ ( s e. ~P U. J /\ ( z e. u /\ u C_ s /\ ( J ↾t s ) e. PConn ) ) ) /\ ( ( w e. u /\ ( g e. ( II Cn J ) /\ ( ( g ` 0 ) = x /\ ( g ` 1 ) = w ) ) ) /\ y e. u ) ) /\ ( h e. ( II Cn ( J ↾t s ) ) /\ ( ( h ` 0 ) = w /\ ( h ` 1 ) = y ) ) ) -> h e. ( II Cn J ) )
45 simplrr 801 . . . . . . . . . . . . . . . . . . . . . . . . . . . . 29 |- ( ( ( w e. u /\ ( g e. ( II Cn J ) /\ ( ( g ` 0 ) = x /\ ( g ` 1 ) = w ) ) ) /\ y e. u ) -> ( ( g ` 0 ) = x /\ ( g ` 1 ) = w ) )
4645ad2antlr 763 . . . . . . . . . . . . . . . . . . . . . . . . . . . 28 |- ( ( ( ( ( ( J e. Conn /\ J e. 𝑛Locally PConn ) /\ ( x e. U. J /\ z e. U. J ) ) /\ ( s e. ~P U. J /\ ( z e. u /\ u C_ s /\ ( J ↾t s ) e. PConn ) ) ) /\ ( ( w e. u /\ ( g e. ( II Cn J ) /\ ( ( g ` 0 ) = x /\ ( g ` 1 ) = w ) ) ) /\ y e. u ) ) /\ ( h e. ( II Cn ( J ↾t s ) ) /\ ( ( h ` 0 ) = w /\ ( h ` 1 ) = y ) ) ) -> ( ( g ` 0 ) = x /\ ( g ` 1 ) = w ) )
4746simprd 479 . . . . . . . . . . . . . . . . . . . . . . . . . . 27 |- ( ( ( ( ( ( J e. Conn /\ J e. 𝑛Locally PConn ) /\ ( x e. U. J /\ z e. U. J ) ) /\ ( s e. ~P U. J /\ ( z e. u /\ u C_ s /\ ( J ↾t s ) e. PConn ) ) ) /\ ( ( w e. u /\ ( g e. ( II Cn J ) /\ ( ( g ` 0 ) = x /\ ( g ` 1 ) = w ) ) ) /\ y e. u ) ) /\ ( h e. ( II Cn ( J ↾t s ) ) /\ ( ( h ` 0 ) = w /\ ( h ` 1 ) = y ) ) ) -> ( g ` 1 ) = w )
48 simprrl 804 . . . . . . . . . . . . . . . . . . . . . . . . . . 27 |- ( ( ( ( ( ( J e. Conn /\ J e. 𝑛Locally PConn ) /\ ( x e. U. J /\ z e. U. J ) ) /\ ( s e. ~P U. J /\ ( z e. u /\ u C_ s /\ ( J ↾t s ) e. PConn ) ) ) /\ ( ( w e. u /\ ( g e. ( II Cn J ) /\ ( ( g ` 0 ) = x /\ ( g ` 1 ) = w ) ) ) /\ y e. u ) ) /\ ( h e. ( II Cn ( J ↾t s ) ) /\ ( ( h ` 0 ) = w /\ ( h ` 1 ) = y ) ) ) -> ( h ` 0 ) = w )
4947, 48eqtr4d 2659 . . . . . . . . . . . . . . . . . . . . . . . . . 26 |- ( ( ( ( ( ( J e. Conn /\ J e. 𝑛Locally PConn ) /\ ( x e. U. J /\ z e. U. J ) ) /\ ( s e. ~P U. J /\ ( z e. u /\ u C_ s /\ ( J ↾t s ) e. PConn ) ) ) /\ ( ( w e. u /\ ( g e. ( II Cn J ) /\ ( ( g ` 0 ) = x /\ ( g ` 1 ) = w ) ) ) /\ y e. u ) ) /\ ( h e. ( II Cn ( J ↾t s ) ) /\ ( ( h ` 0 ) = w /\ ( h ` 1 ) = y ) ) ) -> ( g ` 1 ) = ( h ` 0 ) )
5039, 44, 49pcocn 22817 . . . . . . . . . . . . . . . . . . . . . . . . 25 |- ( ( ( ( ( ( J e. Conn /\ J e. 𝑛Locally PConn ) /\ ( x e. U. J /\ z e. U. J ) ) /\ ( s e. ~P U. J /\ ( z e. u /\ u C_ s /\ ( J ↾t s ) e. PConn ) ) ) /\ ( ( w e. u /\ ( g e. ( II Cn J ) /\ ( ( g ` 0 ) = x /\ ( g ` 1 ) = w ) ) ) /\ y e. u ) ) /\ ( h e. ( II Cn ( J ↾t s ) ) /\ ( ( h ` 0 ) = w /\ ( h ` 1 ) = y ) ) ) -> ( g ( *p ` J ) h ) e. ( II Cn J ) )
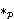5139, 44pco0 22814 . . . . . . . . . . . . . . . . . . . . . . . . . 26 |- ( ( ( ( ( ( J e. Conn /\ J e. 𝑛Locally PConn ) /\ ( x e. U. J /\ z e. U. J ) ) /\ ( s e. ~P U. J /\ ( z e. u /\ u C_ s /\ ( J ↾t s ) e. PConn ) ) ) /\ ( ( w e. u /\ ( g e. ( II Cn J ) /\ ( ( g ` 0 ) = x /\ ( g ` 1 ) = w ) ) ) /\ y e. u ) ) /\ ( h e. ( II Cn ( J ↾t s ) ) /\ ( ( h ` 0 ) = w /\ ( h ` 1 ) = y ) ) ) -> ( ( g ( *p ` J ) h ) ` 0 ) = ( g ` 0 ) )
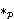5246simpld 475 . . . . . . . . . . . . . . . . . . . . . . . . . 26 |- ( ( ( ( ( ( J e. Conn /\ J e. 𝑛Locally PConn ) /\ ( x e. U. J /\ z e. U. J ) ) /\ ( s e. ~P U. J /\ ( z e. u /\ u C_ s /\ ( J ↾t s ) e. PConn ) ) ) /\ ( ( w e. u /\ ( g e. ( II Cn J ) /\ ( ( g ` 0 ) = x /\ ( g ` 1 ) = w ) ) ) /\ y e. u ) ) /\ ( h e. ( II Cn ( J ↾t s ) ) /\ ( ( h ` 0 ) = w /\ ( h ` 1 ) = y ) ) ) -> ( g ` 0 ) = x )
5351, 52eqtrd 2656 . . . . . . . . . . . . . . . . . . . . . . . . 25 |- ( ( ( ( ( ( J e. Conn /\ J e. 𝑛Locally PConn ) /\ ( x e. U. J /\ z e. U. J ) ) /\ ( s e. ~P U. J /\ ( z e. u /\ u C_ s /\ ( J ↾t s ) e. PConn ) ) ) /\ ( ( w e. u /\ ( g e. ( II Cn J ) /\ ( ( g ` 0 ) = x /\ ( g ` 1 ) = w ) ) ) /\ y e. u ) ) /\ ( h e. ( II Cn ( J ↾t s ) ) /\ ( ( h ` 0 ) = w /\ ( h ` 1 ) = y ) ) ) -> ( ( g ( *p ` J ) h ) ` 0 ) = x )
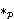5439, 44pco1 22815 . . . . . . . . . . . . . . . . . . . . . . . . . 26 |- ( ( ( ( ( ( J e. Conn /\ J e. 𝑛Locally PConn ) /\ ( x e. U. J /\ z e. U. J ) ) /\ ( s e. ~P U. J /\ ( z e. u /\ u C_ s /\ ( J ↾t s ) e. PConn ) ) ) /\ ( ( w e. u /\ ( g e. ( II Cn J ) /\ ( ( g ` 0 ) = x /\ ( g ` 1 ) = w ) ) ) /\ y e. u ) ) /\ ( h e. ( II Cn ( J ↾t s ) ) /\ ( ( h ` 0 ) = w /\ ( h ` 1 ) = y ) ) ) -> ( ( g ( *p ` J ) h ) ` 1 ) = ( h ` 1 ) )
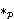55 simprrr 805 . . . . . . . . . . . . . . . . . . . . . . . . . 26 |- ( ( ( ( ( ( J e. Conn /\ J e. 𝑛Locally PConn ) /\ ( x e. U. J /\ z e. U. J ) ) /\ ( s e. ~P U. J /\ ( z e. u /\ u C_ s /\ ( J ↾t s ) e. PConn ) ) ) /\ ( ( w e. u /\ ( g e. ( II Cn J ) /\ ( ( g ` 0 ) = x /\ ( g ` 1 ) = w ) ) ) /\ y e. u ) ) /\ ( h e. ( II Cn ( J ↾t s ) ) /\ ( ( h ` 0 ) = w /\ ( h ` 1 ) = y ) ) ) -> ( h ` 1 ) = y )
5654, 55eqtrd 2656 . . . . . . . . . . . . . . . . . . . . . . . . 25 |- ( ( ( ( ( ( J e. Conn /\ J e. 𝑛Locally PConn ) /\ ( x e. U. J /\ z e. U. J ) ) /\ ( s e. ~P U. J /\ ( z e. u /\ u C_ s /\ ( J ↾t s ) e. PConn ) ) ) /\ ( ( w e. u /\ ( g e. ( II Cn J ) /\ ( ( g ` 0 ) = x /\ ( g ` 1 ) = w ) ) ) /\ y e. u ) ) /\ ( h e. ( II Cn ( J ↾t s ) ) /\ ( ( h ` 0 ) = w /\ ( h ` 1 ) = y ) ) ) -> ( ( g ( *p ` J ) h ) ` 1 ) = y )
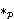57 fveq1 6190 . . . . . . . . . . . . . . . . . . . . . . . . . . . 28 |- ( f = ( g ( *p ` J ) h ) -> ( f ` 0 ) = ( ( g ( *p ` J ) h ) ` 0 ) )
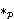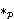5857eqeq1d 2624 . . . . . . . . . . . . . . . . . . . . . . . . . . 27 |- ( f = ( g ( *p ` J ) h ) -> ( ( f ` 0 ) = x <-> ( ( g ( *p ` J ) h ) ` 0 ) = x ) )
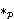
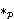59 fveq1 6190 . . . . . . . . . . . . . . . . . . . . . . . . . . . 28 |- ( f = ( g ( *p ` J ) h ) -> ( f ` 1 ) = ( ( g ( *p ` J ) h ) ` 1 ) )
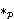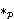6059eqeq1d 2624 . . . . . . . . . . . . . . . . . . . . . . . . . . 27 |- ( f = ( g ( *p ` J ) h ) -> ( ( f ` 1 ) = y <-> ( ( g ( *p ` J ) h ) ` 1 ) = y ) )
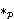
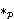6158, 60anbi12d 747 . . . . . . . . . . . . . . . . . . . . . . . . . 26 |- ( f = ( g ( *p ` J ) h ) -> ( ( ( f ` 0 ) = x /\ ( f ` 1 ) = y ) <-> ( ( ( g ( *p ` J ) h ) ` 0 ) = x /\ ( ( g ( *p ` J ) h ) ` 1 ) = y ) ) )
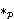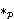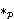6261rspcev 3309 . . . . . . . . . . . . . . . . . . . . . . . . 25 |- ( ( ( g ( *p ` J ) h ) e. ( II Cn J ) /\ ( ( ( g ( *p ` J ) h ) ` 0 ) = x /\ ( ( g ( *p ` J ) h ) ` 1 ) = y ) ) -> E. f e. ( II Cn J ) ( ( f ` 0 ) = x /\ ( f ` 1 ) = y ) )
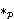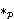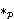6350, 53, 56, 62syl12anc 1324 . . . . . . . . . . . . . . . . . . . . . . . 24 |- ( ( ( ( ( ( J e. Conn /\ J e. 𝑛Locally PConn ) /\ ( x e. U. J /\ z e. U. J ) ) /\ ( s e. ~P U. J /\ ( z e. u /\ u C_ s /\ ( J ↾t s ) e. PConn ) ) ) /\ ( ( w e. u /\ ( g e. ( II Cn J ) /\ ( ( g ` 0 ) = x /\ ( g ` 1 ) = w ) ) ) /\ y e. u ) ) /\ ( h e. ( II Cn ( J ↾t s ) ) /\ ( ( h ` 0 ) = w /\ ( h ` 1 ) = y ) ) ) -> E. f e. ( II Cn J ) ( ( f ` 0 ) = x /\ ( f ` 1 ) = y ) )
6437, 63rexlimddv 3035 . . . . . . . . . . . . . . . . . . . . . . 23 |- ( ( ( ( ( J e. Conn /\ J e. 𝑛Locally PConn ) /\ ( x e. U. J /\ z e. U. J ) ) /\ ( s e. ~P U. J /\ ( z e. u /\ u C_ s /\ ( J ↾t s ) e. PConn ) ) ) /\ ( ( w e. u /\ ( g e. ( II Cn J ) /\ ( ( g ` 0 ) = x /\ ( g ` 1 ) = w ) ) ) /\ y e. u ) ) -> E. f e. ( II Cn J ) ( ( f ` 0 ) = x /\ ( f ` 1 ) = y ) )
6564anassrs 680 . . . . . . . . . . . . . . . . . . . . . 22 |- ( ( ( ( ( ( J e. Conn /\ J e. 𝑛Locally PConn ) /\ ( x e. U. J /\ z e. U. J ) ) /\ ( s e. ~P U. J /\ ( z e. u /\ u C_ s /\ ( J ↾t s ) e. PConn ) ) ) /\ ( w e. u /\ ( g e. ( II Cn J ) /\ ( ( g ` 0 ) = x /\ ( g ` 1 ) = w ) ) ) ) /\ y e. u ) -> E. f e. ( II Cn J ) ( ( f ` 0 ) = x /\ ( f ` 1 ) = y ) )
6665ralrimiva 2966 . . . . . . . . . . . . . . . . . . . . 21 |- ( ( ( ( ( J e. Conn /\ J e. 𝑛Locally PConn ) /\ ( x e. U. J /\ z e. U. J ) ) /\ ( s e. ~P U. J /\ ( z e. u /\ u C_ s /\ ( J ↾t s ) e. PConn ) ) ) /\ ( w e. u /\ ( g e. ( II Cn J ) /\ ( ( g ` 0 ) = x /\ ( g ` 1 ) = w ) ) ) ) -> A. y e. u E. f e. ( II Cn J ) ( ( f ` 0 ) = x /\ ( f ` 1 ) = y ) )
6766anassrs 680 . . . . . . . . . . . . . . . . . . . 20 |- ( ( ( ( ( ( J e. Conn /\ J e. 𝑛Locally PConn ) /\ ( x e. U. J /\ z e. U. J ) ) /\ ( s e. ~P U. J /\ ( z e. u /\ u C_ s /\ ( J ↾t s ) e. PConn ) ) ) /\ w e. u ) /\ ( g e. ( II Cn J ) /\ ( ( g ` 0 ) = x /\ ( g ` 1 ) = w ) ) ) -> A. y e. u E. f e. ( II Cn J ) ( ( f ` 0 ) = x /\ ( f ` 1 ) = y ) )
6867rexlimdvaa 3032 . . . . . . . . . . . . . . . . . . 19 |- ( ( ( ( ( J e. Conn /\ J e. 𝑛Locally PConn ) /\ ( x e. U. J /\ z e. U. J ) ) /\ ( s e. ~P U. J /\ ( z e. u /\ u C_ s /\ ( J ↾t s ) e. PConn ) ) ) /\ w e. u ) -> ( E. g e. ( II Cn J ) ( ( g ` 0 ) = x /\ ( g ` 1 ) = w ) -> A. y e. u E. f e. ( II Cn J ) ( ( f ` 0 ) = x /\ ( f ` 1 ) = y ) ) )
6921adantr 481 . . . . . . . . . . . . . . . . . . . 20 |- ( ( ( ( ( J e. Conn /\ J e. 𝑛Locally PConn ) /\ ( x e. U. J /\ z e. U. J ) ) /\ ( s e. ~P U. J /\ ( z e. u /\ u C_ s /\ ( J ↾t s ) e. PConn ) ) ) /\ w e. u ) -> u C_ s )
70 simplrl 800 . . . . . . . . . . . . . . . . . . . . 21 |- ( ( ( ( ( J e. Conn /\ J e. 𝑛Locally PConn ) /\ ( x e. U. J /\ z e. U. J ) ) /\ ( s e. ~P U. J /\ ( z e. u /\ u C_ s /\ ( J ↾t s ) e. PConn ) ) ) /\ w e. u ) -> s e. ~P U. J )
7170, 26syl 17 . . . . . . . . . . . . . . . . . . . 20 |- ( ( ( ( ( J e. Conn /\ J e. 𝑛Locally PConn ) /\ ( x e. U. J /\ z e. U. J ) ) /\ ( s e. ~P U. J /\ ( z e. u /\ u C_ s /\ ( J ↾t s ) e. PConn ) ) ) /\ w e. u ) -> s C_ U. J )
7269, 71sstrd 3613 . . . . . . . . . . . . . . . . . . 19 |- ( ( ( ( ( J e. Conn /\ J e. 𝑛Locally PConn ) /\ ( x e. U. J /\ z e. U. J ) ) /\ ( s e. ~P U. J /\ ( z e. u /\ u C_ s /\ ( J ↾t s ) e. PConn ) ) ) /\ w e. u ) -> u C_ U. J )
7368, 72jctild 566 . . . . . . . . . . . . . . . . . 18 |- ( ( ( ( ( J e. Conn /\ J e. 𝑛Locally PConn ) /\ ( x e. U. J /\ z e. U. J ) ) /\ ( s e. ~P U. J /\ ( z e. u /\ u C_ s /\ ( J ↾t s ) e. PConn ) ) ) /\ w e. u ) -> ( E. g e. ( II Cn J ) ( ( g ` 0 ) = x /\ ( g ` 1 ) = w ) -> ( u C_ U. J /\ A. y e. u E. f e. ( II Cn J ) ( ( f ` 0 ) = x /\ ( f ` 1 ) = y ) ) ) )
74 fveq1 6190 . . . . . . . . . . . . . . . . . . . . 21 |- ( f = g -> ( f ` 0 ) = ( g ` 0 ) )
7574eqeq1d 2624 . . . . . . . . . . . . . . . . . . . 20 |- ( f = g -> ( ( f ` 0 ) = x <-> ( g ` 0 ) = x ) )
76 fveq1 6190 . . . . . . . . . . . . . . . . . . . . 21 |- ( f = g -> ( f ` 1 ) = ( g ` 1 ) )
7776eqeq1d 2624 . . . . . . . . . . . . . . . . . . . 20 |- ( f = g -> ( ( f ` 1 ) = w <-> ( g ` 1 ) = w ) )
7875, 77anbi12d 747 . . . . . . . . . . . . . . . . . . 19 |- ( f = g -> ( ( ( f ` 0 ) = x /\ ( f ` 1 ) = w ) <-> ( ( g ` 0 ) = x /\ ( g ` 1 ) = w ) ) )
7978cbvrexv 3172 . . . . . . . . . . . . . . . . . 18 |- ( E. f e. ( II Cn J ) ( ( f ` 0 ) = x /\ ( f ` 1 ) = w ) <-> E. g e. ( II Cn J ) ( ( g ` 0 ) = x /\ ( g ` 1 ) = w ) )
80 ssrab 3680 . . . . . . . . . . . . . . . . . 18 |- ( u C_ { y e. U. J | E. f e. ( II Cn J ) ( ( f ` 0 ) = x /\ ( f ` 1 ) = y ) } <-> ( u C_ U. J /\ A. y e. u E. f e. ( II Cn J ) ( ( f ` 0 ) = x /\ ( f ` 1 ) = y ) ) )
8173, 79, 803imtr4g 285 . . . . . . . . . . . . . . . . 17 |- ( ( ( ( ( J e. Conn /\ J e. 𝑛Locally PConn ) /\ ( x e. U. J /\ z e. U. J ) ) /\ ( s e. ~P U. J /\ ( z e. u /\ u C_ s /\ ( J ↾t s ) e. PConn ) ) ) /\ w e. u ) -> ( E. f e. ( II Cn J ) ( ( f ` 0 ) = x /\ ( f ` 1 ) = w ) -> u C_ { y e. U. J | E. f e. ( II Cn J ) ( ( f ` 0 ) = x /\ ( f ` 1 ) = y ) } ) )
8218, 81syl5 34 . . . . . . . . . . . . . . . 16 |- ( ( ( ( ( J e. Conn /\ J e. 𝑛Locally PConn ) /\ ( x e. U. J /\ z e. U. J ) ) /\ ( s e. ~P U. J /\ ( z e. u /\ u C_ s /\ ( J ↾t s ) e. PConn ) ) ) /\ w e. u ) -> ( w e. { y e. U. J | E. f e. ( II Cn J ) ( ( f ` 0 ) = x /\ ( f ` 1 ) = y ) } -> u C_ { y e. U. J | E. f e. ( II Cn J ) ( ( f ` 0 ) = x /\ ( f ` 1 ) = y ) } ) )
8382ralrimiva 2966 . . . . . . . . . . . . . . 15 |- ( ( ( ( J e. Conn /\ J e. 𝑛Locally PConn ) /\ ( x e. U. J /\ z e. U. J ) ) /\ ( s e. ~P U. J /\ ( z e. u /\ u C_ s /\ ( J ↾t s ) e. PConn ) ) ) -> A. w e. u ( w e. { y e. U. J | E. f e. ( II Cn J ) ( ( f ` 0 ) = x /\ ( f ` 1 ) = y ) } -> u C_ { y e. U. J | E. f e. ( II Cn J ) ( ( f ` 0 ) = x /\ ( f ` 1 ) = y ) } ) )
8413, 83jca 554 . . . . . . . . . . . . . 14 |- ( ( ( ( J e. Conn /\ J e. 𝑛Locally PConn ) /\ ( x e. U. J /\ z e. U. J ) ) /\ ( s e. ~P U. J /\ ( z e. u /\ u C_ s /\ ( J ↾t s ) e. PConn ) ) ) -> ( z e. u /\ A. w e. u ( w e. { y e. U. J | E. f e. ( II Cn J ) ( ( f ` 0 ) = x /\ ( f ` 1 ) = y ) } -> u C_ { y e. U. J | E. f e. ( II Cn J ) ( ( f ` 0 ) = x /\ ( f ` 1 ) = y ) } ) ) )
8584expr 643 . . . . . . . . . . . . 13 |- ( ( ( ( J e. Conn /\ J e. 𝑛Locally PConn ) /\ ( x e. U. J /\ z e. U. J ) ) /\ s e. ~P U. J ) -> ( ( z e. u /\ u C_ s /\ ( J ↾t s ) e. PConn ) -> ( z e. u /\ A. w e. u ( w e. { y e. U. J | E. f e. ( II Cn J ) ( ( f ` 0 ) = x /\ ( f ` 1 ) = y ) } -> u C_ { y e. U. J | E. f e. ( II Cn J ) ( ( f ` 0 ) = x /\ ( f ` 1 ) = y ) } ) ) ) )
8685reximdv 3016 . . . . . . . . . . . 12 |- ( ( ( ( J e. Conn /\ J e. 𝑛Locally PConn ) /\ ( x e. U. J /\ z e. U. J ) ) /\ s e. ~P U. J ) -> ( E. u e. J ( z e. u /\ u C_ s /\ ( J ↾t s ) e. PConn ) -> E. u e. J ( z e. u /\ A. w e. u ( w e. { y e. U. J | E. f e. ( II Cn J ) ( ( f ` 0 ) = x /\ ( f ` 1 ) = y ) } -> u C_ { y e. U. J | E. f e. ( II Cn J ) ( ( f ` 0 ) = x /\ ( f ` 1 ) = y ) } ) ) ) )
8786rexlimdva 3031 . . . . . . . . . . 11 |- ( ( ( J e. Conn /\ J e. 𝑛Locally PConn ) /\ ( x e. U. J /\ z e. U. J ) ) -> ( E. s e. ~P U. J E. u e. J ( z e. u /\ u C_ s /\ ( J ↾t s ) e. PConn ) -> E. u e. J ( z e. u /\ A. w e. u ( w e. { y e. U. J | E. f e. ( II Cn J ) ( ( f ` 0 ) = x /\ ( f ` 1 ) = y ) } -> u C_ { y e. U. J | E. f e. ( II Cn J ) ( ( f ` 0 ) = x /\ ( f ` 1 ) = y ) } ) ) ) )
8812, 87mpd 15 . . . . . . . . . 10 |- ( ( ( J e. Conn /\ J e. 𝑛Locally PConn ) /\ ( x e. U. J /\ z e. U. J ) ) -> E. u e. J ( z e. u /\ A. w e. u ( w e. { y e. U. J | E. f e. ( II Cn J ) ( ( f ` 0 ) = x /\ ( f ` 1 ) = y ) } -> u C_ { y e. U. J | E. f e. ( II Cn J ) ( ( f ` 0 ) = x /\ ( f ` 1 ) = y ) } ) ) )
8988anassrs 680 . . . . . . . . 9 |- ( ( ( ( J e. Conn /\ J e. 𝑛Locally PConn ) /\ x e. U. J ) /\ z e. U. J ) -> E. u e. J ( z e. u /\ A. w e. u ( w e. { y e. U. J | E. f e. ( II Cn J ) ( ( f ` 0 ) = x /\ ( f ` 1 ) = y ) } -> u C_ { y e. U. J | E. f e. ( II Cn J ) ( ( f ` 0 ) = x /\ ( f ` 1 ) = y ) } ) ) )
9089ralrimiva 2966 . . . . . . . 8 |- ( ( ( J e. Conn /\ J e. 𝑛Locally PConn ) /\ x e. U. J ) -> A. z e. U. J E. u e. J ( z e. u /\ A. w e. u ( w e. { y e. U. J | E. f e. ( II Cn J ) ( ( f ` 0 ) = x /\ ( f ` 1 ) = y ) } -> u C_ { y e. U. J | E. f e. ( II Cn J ) ( ( f ` 0 ) = x /\ ( f ` 1 ) = y ) } ) ) )
911ad2antrr 762 . . . . . . . . 9 |- ( ( ( J e. Conn /\ J e. 𝑛Locally PConn ) /\ x e. U. J ) -> J e. Top )
92 ssrab2 3687 . . . . . . . . 9 |- { y e. U. J | E. f e. ( II Cn J ) ( ( f ` 0 ) = x /\ ( f ` 1 ) = y ) } C_ U. J
933isclo2 20892 . . . . . . . . 9 |- ( ( J e. Top /\ { y e. U. J | E. f e. ( II Cn J ) ( ( f ` 0 ) = x /\ ( f ` 1 ) = y ) } C_ U. J ) -> ( { y e. U. J | E. f e. ( II Cn J ) ( ( f ` 0 ) = x /\ ( f ` 1 ) = y ) } e. ( J i^i ( Clsd ` J ) ) <-> A. z e. U. J E. u e. J ( z e. u /\ A. w e. u ( w e. { y e. U. J | E. f e. ( II Cn J ) ( ( f ` 0 ) = x /\ ( f ` 1 ) = y ) } -> u C_ { y e. U. J | E. f e. ( II Cn J ) ( ( f ` 0 ) = x /\ ( f ` 1 ) = y ) } ) ) ) )
9491, 92, 93sylancl 694 . . . . . . . 8 |- ( ( ( J e. Conn /\ J e. 𝑛Locally PConn ) /\ x e. U. J ) -> ( { y e. U. J | E. f e. ( II Cn J ) ( ( f ` 0 ) = x /\ ( f ` 1 ) = y ) } e. ( J i^i ( Clsd ` J ) ) <-> A. z e. U. J E. u e. J ( z e. u /\ A. w e. u ( w e. { y e. U. J | E. f e. ( II Cn J ) ( ( f ` 0 ) = x /\ ( f ` 1 ) = y ) } -> u C_ { y e. U. J | E. f e. ( II Cn J ) ( ( f ` 0 ) = x /\ ( f ` 1 ) = y ) } ) ) ) )
9590, 94mpbird 247 . . . . . . 7 |- ( ( ( J e. Conn /\ J e. 𝑛Locally PConn ) /\ x e. U. J ) -> { y e. U. J | E. f e. ( II Cn J ) ( ( f ` 0 ) = x /\ ( f ` 1 ) = y ) } e. ( J i^i ( Clsd ` J ) ) )
965, 95sseldi 3601 . . . . . 6 |- ( ( ( J e. Conn /\ J e. 𝑛Locally PConn ) /\ x e. U. J ) -> { y e. U. J | E. f e. ( II Cn J ) ( ( f ` 0 ) = x /\ ( f ` 1 ) = y ) } e. J )
97 simpr 477 . . . . . . . 8 |- ( ( ( J e. Conn /\ J e. 𝑛Locally PConn ) /\ x e. U. J ) -> x e. U. J )
98 iitopon 22682 . . . . . . . . . 10 |- II e. (TopOn ` ( 0 [,] 1 ) )
9998a1i 11 . . . . . . . . 9 |- ( ( ( J e. Conn /\ J e. 𝑛Locally PConn ) /\ x e. U. J ) -> II e. (TopOn ` ( 0 [,] 1 ) ) )
1003toptopon 20722 . . . . . . . . . 10 |- ( J e. Top <-> J e. (TopOn ` U. J ) )
10191, 100sylib 208 . . . . . . . . 9 |- ( ( ( J e. Conn /\ J e. 𝑛Locally PConn ) /\ x e. U. J ) -> J e. (TopOn ` U. J ) )
102 cnconst2 21087 . . . . . . . . 9 |- ( ( II e. (TopOn ` ( 0 [,] 1 ) ) /\ J e. (TopOn ` U. J ) /\ x e. U. J ) -> ( ( 0 [,] 1 ) X. { x } ) e. ( II Cn J ) )
10399, 101, 97, 102syl3anc 1326 . . . . . . . 8 |- ( ( ( J e. Conn /\ J e. 𝑛Locally PConn ) /\ x e. U. J ) -> ( ( 0 [,] 1 ) X. { x } ) e. ( II Cn J ) )
104 0elunit 12290 . . . . . . . . 9 |- 0 e. ( 0 [,] 1 )
105 vex 3203 . . . . . . . . . 10 |- x e. _V
106105fvconst2 6469 . . . . . . . . 9 |- ( 0 e. ( 0 [,] 1 ) -> ( ( ( 0 [,] 1 ) X. { x } ) ` 0 ) = x )
107104, 106mp1i 13 . . . . . . . 8 |- ( ( ( J e. Conn /\ J e. 𝑛Locally PConn ) /\ x e. U. J ) -> ( ( ( 0 [,] 1 ) X. { x } ) ` 0 ) = x )
108 1elunit 12291 . . . . . . . . 9 |- 1 e. ( 0 [,] 1 )
109105fvconst2 6469 . . . . . . . . 9 |- ( 1 e. ( 0 [,] 1 ) -> ( ( ( 0 [,] 1 ) X. { x } ) ` 1 ) = x )
110108, 109mp1i 13 . . . . . . . 8 |- ( ( ( J e. Conn /\ J e. 𝑛Locally PConn ) /\ x e. U. J ) -> ( ( ( 0 [,] 1 ) X. { x } ) ` 1 ) = x )
111 eqeq2 2633 . . . . . . . . . 10 |- ( y = x -> ( ( f ` 1 ) = y <-> ( f ` 1 ) = x ) )
112111anbi2d 740 . . . . . . . . 9 |- ( y = x -> ( ( ( f ` 0 ) = x /\ ( f ` 1 ) = y ) <-> ( ( f ` 0 ) = x /\ ( f ` 1 ) = x ) ) )
113 fveq1 6190 . . . . . . . . . . 11 |- ( f = ( ( 0 [,] 1 ) X. { x } ) -> ( f ` 0 ) = ( ( ( 0 [,] 1 ) X. { x } ) ` 0 ) )
114113eqeq1d 2624 . . . . . . . . . 10 |- ( f = ( ( 0 [,] 1 ) X. { x } ) -> ( ( f ` 0 ) = x <-> ( ( ( 0 [,] 1 ) X. { x } ) ` 0 ) = x ) )
115 fveq1 6190 . . . . . . . . . . 11 |- ( f = ( ( 0 [,] 1 ) X. { x } ) -> ( f ` 1 ) = ( ( ( 0 [,] 1 ) X. { x } ) ` 1 ) )
116115eqeq1d 2624 . . . . . . . . . 10 |- ( f = ( ( 0 [,] 1 ) X. { x } ) -> ( ( f ` 1 ) = x <-> ( ( ( 0 [,] 1 ) X. { x } ) ` 1 ) = x ) )
117114, 116anbi12d 747 . . . . . . . . 9 |- ( f = ( ( 0 [,] 1 ) X. { x } ) -> ( ( ( f ` 0 ) = x /\ ( f ` 1 ) = x ) <-> ( ( ( ( 0 [,] 1 ) X. { x } ) ` 0 ) = x /\ ( ( ( 0 [,] 1 ) X. { x } ) ` 1 ) = x ) ) )
118112, 117rspc2ev 3324 . . . . . . . 8 |- ( ( x e. U. J /\ ( ( 0 [,] 1 ) X. { x } ) e. ( II Cn J ) /\ ( ( ( ( 0 [,] 1 ) X. { x } ) ` 0 ) = x /\ ( ( ( 0 [,] 1 ) X. { x } ) ` 1 ) = x ) ) -> E. y e. U. J E. f e. ( II Cn J ) ( ( f ` 0 ) = x /\ ( f ` 1 ) = y ) )
11997, 103, 107, 110, 118syl112anc 1330 . . . . . . 7 |- ( ( ( J e. Conn /\ J e. 𝑛Locally PConn ) /\ x e. U. J ) -> E. y e. U. J E. f e. ( II Cn J ) ( ( f ` 0 ) = x /\ ( f ` 1 ) = y ) )
120 rabn0 3958 . . . . . . 7 |- ( { y e. U. J | E. f e. ( II Cn J ) ( ( f ` 0 ) = x /\ ( f ` 1 ) = y ) } =/= (/) <-> E. y e. U. J E. f e. ( II Cn J ) ( ( f ` 0 ) = x /\ ( f ` 1 ) = y ) )
121119, 120sylibr 224 . . . . . 6 |- ( ( ( J e. Conn /\ J e. 𝑛Locally PConn ) /\ x e. U. J ) -> { y e. U. J | E. f e. ( II Cn J ) ( ( f ` 0 ) = x /\ ( f ` 1 ) = y ) } =/= (/) )
122 inss2 3834 . . . . . . 7 |- ( J i^i ( Clsd ` J ) ) C_ ( Clsd ` J )
123122, 95sseldi 3601 . . . . . 6 |- ( ( ( J e. Conn /\ J e. 𝑛Locally PConn ) /\ x e. U. J ) -> { y e. U. J | E. f e. ( II Cn J ) ( ( f ` 0 ) = x /\ ( f ` 1 ) = y ) } e. ( Clsd ` J ) )
1243, 4, 96, 121, 123connclo 21218 . . . . 5 |- ( ( ( J e. Conn /\ J e. 𝑛Locally PConn ) /\ x e. U. J ) -> { y e. U. J | E. f e. ( II Cn J ) ( ( f ` 0 ) = x /\ ( f ` 1 ) = y ) } = U. J )
125124eqcomd 2628 . . . 4 |- ( ( ( J e. Conn /\ J e. 𝑛Locally PConn ) /\ x e. U. J ) -> U. J = { y e. U. J | E. f e. ( II Cn J ) ( ( f ` 0 ) = x /\ ( f ` 1 ) = y ) } )
126 rabid2 3118 . . . 4 |- ( U. J = { y e. U. J | E. f e. ( II Cn J ) ( ( f ` 0 ) = x /\ ( f ` 1 ) = y ) } <-> A. y e. U. J E. f e. ( II Cn J ) ( ( f ` 0 ) = x /\ ( f ` 1 ) = y ) )
127125, 126sylib 208 . . 3 |- ( ( ( J e. Conn /\ J e. 𝑛Locally PConn ) /\ x e. U. J ) -> A. y e. U. J E. f e. ( II Cn J ) ( ( f ` 0 ) = x /\ ( f ` 1 ) = y ) )
128127ralrimiva 2966 . 2 |- ( ( J e. Conn /\ J e. 𝑛Locally PConn ) -> A. x e. U. J A. y e. U. J E. f e. ( II Cn J ) ( ( f ` 0 ) = x /\ ( f ` 1 ) = y ) )
1293ispconn 31205 . 2 |- ( J e. PConn <-> ( J e. Top /\ A. x e. U. J A. y e. U. J E. f e. ( II Cn J ) ( ( f ` 0 ) = x /\ ( f ` 1 ) = y ) ) )
1302, 128, 129sylanbrc 698 1 |- ( ( J e. Conn /\ J e. 𝑛Locally PConn ) -> J e. PConn )
Colors of variables: wff setvar class
Syntax hints:   -> wi 4   <-> wb 196   /\ wa 384   /\ w3a 1037   = wceq 1483   e. wcel 1990   =/= wne 2794   A.wral 2912   E.wrex 2913   {crab 2916   i^i cin 3573   C_ wss 3574   (/)c0 3915   ~Pcpw 4158   {csn 4177   U.cuni 4436   X. cxp 5112   ` cfv 5888  (class class class)co 6650   0cc0 9936   1c1 9937   [,]cicc 12178   ↾t crest 16081   Topctop 20698  TopOnctopon 20715   Clsdccld 20820   Cn ccn 21028  Conncconn 21214  𝑛Locally cnlly 21268   IIcii 22678   *pcpco 22800  PConncpconn 31201
This theorem was proved from axioms:  ax-mp 5  ax-1 6  ax-2 7  ax-3 8  ax-gen 1722  ax-4 1737  ax-5 1839  ax-6 1888  ax-7 1935  ax-8 1992  ax-9 1999  ax-10 2019  ax-11 2034  ax-12 2047  ax-13 2246  ax-ext 2602  ax-rep 4771  ax-sep 4781  ax-nul 4789  ax-pow 4843  ax-pr 4906  ax-un 6949  ax-inf2 8538  ax-cnex 9992  ax-resscn 9993  ax-1cn 9994  ax-icn 9995  ax-addcl 9996  ax-addrcl 9997  ax-mulcl 9998  ax-mulrcl 9999  ax-mulcom 10000  ax-addass 10001  ax-mulass 10002  ax-distr 10003  ax-i2m1 10004  ax-1ne0 10005  ax-1rid 10006  ax-rnegex 10007  ax-rrecex 10008  ax-cnre 10009  ax-pre-lttri 10010  ax-pre-lttrn 10011  ax-pre-ltadd 10012  ax-pre-mulgt0 10013  ax-pre-sup 10014  ax-mulf 10016
This theorem depends on definitions:  df-bi 197  df-or 385  df-an 386  df-3or 1038  df-3an 1039  df-tru 1486  df-ex 1705  df-nf 1710  df-sb 1881  df-eu 2474  df-mo 2475  df-clab 2609  df-cleq 2615  df-clel 2618  df-nfc 2753  df-ne 2795  df-nel 2898  df-ral 2917  df-rex 2918  df-reu 2919  df-rmo 2920  df-rab 2921  df-v 3202  df-sbc 3436  df-csb 3534  df-dif 3577  df-un 3579  df-in 3581  df-ss 3588  df-pss 3590  df-nul 3916  df-if 4087  df-pw 4160  df-sn 4178  df-pr 4180  df-tp 4182  df-op 4184  df-uni 4437  df-int 4476  df-iun 4522  df-iin 4523  df-br 4654  df-opab 4713  df-mpt 4730  df-tr 4753  df-id 5024  df-eprel 5029  df-po 5035  df-so 5036  df-fr 5073  df-se 5074  df-we 5075  df-xp 5120  df-rel 5121  df-cnv 5122  df-co 5123  df-dm 5124  df-rn 5125  df-res 5126  df-ima 5127  df-pred 5680  df-ord 5726  df-on 5727  df-lim 5728  df-suc 5729  df-iota 5851  df-fun 5890  df-fn 5891  df-f 5892  df-f1 5893  df-fo 5894  df-f1o 5895  df-fv 5896  df-isom 5897  df-riota 6611  df-ov 6653  df-oprab 6654  df-mpt2 6655  df-of 6897  df-om 7066  df-1st 7168  df-2nd 7169  df-supp 7296  df-wrecs 7407  df-recs 7468  df-rdg 7506  df-1o 7560  df-2o 7561  df-oadd 7564  df-er 7742  df-map 7859  df-ixp 7909  df-en 7956  df-dom 7957  df-sdom 7958  df-fin 7959  df-fsupp 8276  df-fi 8317  df-sup 8348  df-inf 8349  df-oi 8415  df-card 8765  df-cda 8990  df-pnf 10076  df-mnf 10077  df-xr 10078  df-ltxr 10079  df-le 10080  df-sub 10268  df-neg 10269  df-div 10685  df-nn 11021  df-2 11079  df-3 11080  df-4 11081  df-5 11082  df-6 11083  df-7 11084  df-8 11085  df-9 11086  df-n0 11293  df-z 11378  df-dec 11494  df-uz 11688  df-q 11789  df-rp 11833  df-xneg 11946  df-xadd 11947  df-xmul 11948  df-ioo 12179  df-icc 12182  df-fz 12327  df-fzo 12466  df-seq 12802  df-exp 12861  df-hash 13118  df-cj 13839  df-re 13840  df-im 13841  df-sqrt 13975  df-abs 13976  df-struct 15859  df-ndx 15860  df-slot 15861  df-base 15863  df-sets 15864  df-ress 15865  df-plusg 15954  df-mulr 15955  df-starv 15956  df-sca 15957  df-vsca 15958  df-ip 15959  df-tset 15960  df-ple 15961  df-ds 15964  df-unif 15965  df-hom 15966  df-cco 15967  df-rest 16083  df-topn 16084  df-0g 16102  df-gsum 16103  df-topgen 16104  df-pt 16105  df-prds 16108  df-xrs 16162  df-qtop 16167  df-imas 16168  df-xps 16170  df-mre 16246  df-mrc 16247  df-acs 16249  df-mgm 17242  df-sgrp 17284  df-mnd 17295  df-submnd 17336  df-mulg 17541  df-cntz 17750  df-cmn 18195  df-psmet 19738  df-xmet 19739  df-met 19740  df-bl 19741  df-mopn 19742  df-cnfld 19747  df-top 20699  df-topon 20716  df-topsp 20737  df-bases 20750  df-cld 20823  df-nei 20902  df-cn 21031  df-cnp 21032  df-conn 21215  df-nlly 21270  df-tx 21365  df-hmeo 21558  df-xms 22125  df-ms 22126  df-tms 22127  df-ii 22680  df-pco 22805  df-pconn 31203
This theorem is referenced by: (None)
  Copyright terms: Public domain W3C validator