Proof of Theorem sylow1lem5
| Step | Hyp | Ref
| Expression |
|---|
| 1 | | sylow1.x |
. . . 4
        |
| 2 | | sylow1.g |
. . . 4
        |
| 3 | | sylow1.f |
. . . 4
        |
| 4 | | sylow1.p |
. . . 4
        |
| 5 | | sylow1.n |
. . . 4
        |
| 6 | | sylow1.d |
. . . 4
         
      |
| 7 | | sylow1lem.a |
. . . 4
        |
| 8 | | sylow1lem.s |
. . . 4
        
            |
| 9 | | sylow1lem.m |
. . . 4
                         |
| 10 | 1, 2, 3, 4, 5, 6, 7, 8, 9 | sylow1lem2 18014 |
. . 3
     
  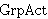    |
| 11 | | sylow1lem4.b |
. . 3
        |
| 12 | | sylow1lem4.h |
. . . 4
                |
| 13 | 1, 12 | gastacl 17742 |
. . 3
    
  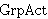            SubGrp SubGrp    |
| 14 | 10, 11, 13 | syl2anc 693 |
. 2
       SubGrp SubGrp    |
| 15 | | sylow1lem3.1 |
. . . 4
         
           
          |
| 16 | 1, 2, 3, 4, 5, 6, 7, 8, 9, 15,
11, 12 | sylow1lem4 18016 |
. . 3
         
      |
| 17 | | sylow1lem5.l |
. . . . . . . 8
            ![] ]](rbrack.gif)                   |
| 18 | 15, 1 | gaorber 17741 |
. . . . . . . . . . . . . . . 16
      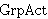    
   |
| 19 | 10, 18 | syl 17 |
. . . . . . . . . . . . . . 15
        |
| 20 | | erdm 7752 |
. . . . . . . . . . . . . . 15
    
      |
| 21 | 19, 20 | syl 17 |
. . . . . . . . . . . . . 14
         |
| 22 | 11, 21 | eleqtrrd 2704 |
. . . . . . . . . . . . 13
         |
| 23 | | ecdmn0 7789 |
. . . . . . . . . . . . 13
      
  ![] ]](rbrack.gif)     |
| 24 | 22, 23 | sylib 208 |
. . . . . . . . . . . 12
      ![] ]](rbrack.gif)     |
| 25 | | pwfi 8261 |
. . . . . . . . . . . . . . . 16
     
     |
| 26 | 3, 25 | sylib 208 |
. . . . . . . . . . . . . . 15
         |
| 27 | | ssrab2 3687 |
. . . . . . . . . . . . . . . 16
                      |
| 28 | 8, 27 | eqsstri 3635 |
. . . . . . . . . . . . . . 15
     |
| 29 | | ssfi 8180 |
. . . . . . . . . . . . . . 15
         
   
    |
| 30 | 26, 28, 29 | sylancl 694 |
. . . . . . . . . . . . . 14
        |
| 31 | 19 | ecss 7788 |
. . . . . . . . . . . . . 14
      ![] ]](rbrack.gif)     |
| 32 | | ssfi 8180 |
. . . . . . . . . . . . . 14
         ![] ]](rbrack.gif)     
  ![] ]](rbrack.gif)     |
| 33 | 30, 31, 32 | syl2anc 693 |
. . . . . . . . . . . . 13
      ![] ]](rbrack.gif)     |
| 34 | | hashnncl 13157 |
. . . . . . . . . . . . 13
    ![] ]](rbrack.gif)           ![] ]](rbrack.gif)   
 
  ![] ]](rbrack.gif)      |
| 35 | 33, 34 | syl 17 |
. . . . . . . . . . . 12
          ![] ]](rbrack.gif)
       ![] ]](rbrack.gif)      |
| 36 | 24, 35 | mpbird 247 |
. . . . . . . . . . 11
         ![] ]](rbrack.gif)
     |
| 37 | 4, 36 | pccld 15555 |
. . . . . . . . . 10
            ![] ]](rbrack.gif)       |
| 38 | 37 | nn0red 11352 |
. . . . . . . . 9
            ![] ]](rbrack.gif)       |
| 39 | 5 | nn0red 11352 |
. . . . . . . . 9
        |
| 40 | 1 | grpbn0 17451 |
. . . . . . . . . . . . 13
          |
| 41 | 2, 40 | syl 17 |
. . . . . . . . . . . 12
        |
| 42 | | hashnncl 13157 |
. . . . . . . . . . . . 13
              
     |
| 43 | 3, 42 | syl 17 |
. . . . . . . . . . . 12
            
     |
| 44 | 41, 43 | mpbird 247 |
. . . . . . . . . . 11
            |
| 45 | 4, 44 | pccld 15555 |
. . . . . . . . . 10
                |
| 46 | 45 | nn0red 11352 |
. . . . . . . . 9
                |
| 47 | | leaddsub 10504 |
. . . . . . . . 9
           ![] ]](rbrack.gif)            
                     ![] ]](rbrack.gif)                 
        ![] ]](rbrack.gif)
   
               |
| 48 | 38, 39, 46, 47 | syl3anc 1326 |
. . . . . . . 8
              ![] ]](rbrack.gif)
                         ![] ]](rbrack.gif)                    |
| 49 | 17, 48 | mpbird 247 |
. . . . . . 7
             ![] ]](rbrack.gif)                  |
| 50 | | eqid 2622 |
. . . . . . . . . . 11
   ~QG ~QG      ~QG ~QG   |
| 51 | 1, 12, 50, 15 | orbsta2 17747 |
. . . . . . . . . 10
    
   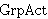     
   
                ![] ]](rbrack.gif)           |
| 52 | 10, 11, 3, 51 | syl21anc 1325 |
. . . . . . . . 9
                ![] ]](rbrack.gif)           |
| 53 | 52 | oveq2d 6666 |
. . . . . . . 8
                       ![] ]](rbrack.gif)
           |
| 54 | 36 | nnzd 11481 |
. . . . . . . . 9
         ![] ]](rbrack.gif)
     |
| 55 | 36 | nnne0d 11065 |
. . . . . . . . 9
         ![] ]](rbrack.gif)
     |
| 56 | | eqid 2622 |
. . . . . . . . . . . . . 14
            |
| 57 | 56 | subg0cl 17602 |
. . . . . . . . . . . . 13
     SubGrp SubGrp   
        |
| 58 | 14, 57 | syl 17 |
. . . . . . . . . . . 12
            |
| 59 | | ne0i 3921 |
. . . . . . . . . . . 12
              |
| 60 | 58, 59 | syl 17 |
. . . . . . . . . . 11
        |
| 61 | | ssrab2 3687 |
. . . . . . . . . . . . . 14
    
           |
| 62 | 12, 61 | eqsstri 3635 |
. . . . . . . . . . . . 13
    |
| 63 | | ssfi 8180 |
. . . . . . . . . . . . 13
             
  |
| 64 | 3, 62, 63 | sylancl 694 |
. . . . . . . . . . . 12
        |
| 65 | | hashnncl 13157 |
. . . . . . . . . . . 12
              
     |
| 66 | 64, 65 | syl 17 |
. . . . . . . . . . 11
            
     |
| 67 | 60, 66 | mpbird 247 |
. . . . . . . . . 10
            |
| 68 | 67 | nnzd 11481 |
. . . . . . . . 9
            |
| 69 | 67 | nnne0d 11065 |
. . . . . . . . 9
            |
| 70 | | pcmul 15556 |
. . . . . . . . 9
             ![] ]](rbrack.gif)           ![] ]](rbrack.gif)
                                  ![] ]](rbrack.gif)               
     ![] ]](rbrack.gif)
               |
| 71 | 4, 54, 55, 68, 69, 70 | syl122anc 1335 |
. . . . . . . 8
             ![] ]](rbrack.gif)               
     ![] ]](rbrack.gif)
               |
| 72 | 53, 71 | eqtrd 2656 |
. . . . . . 7
                       ![] ]](rbrack.gif)
               |
| 73 | 49, 72 | breqtrd 4679 |
. . . . . 6
             ![] ]](rbrack.gif)                 ![] ]](rbrack.gif)       
        |
| 74 | 4, 67 | pccld 15555 |
. . . . . . . 8
                |
| 75 | 74 | nn0red 11352 |
. . . . . . 7
                |
| 76 | 39, 75, 38 | leadd2d 10622 |
. . . . . 6
                
         ![] ]](rbrack.gif)
                ![] ]](rbrack.gif)
                |
| 77 | 73, 76 | mpbird 247 |
. . . . 5
     
          |
| 78 | | pcdvdsb 15573 |
. . . . . 6
                                              |
| 79 | 4, 68, 5, 78 | syl3anc 1326 |
. . . . 5
                
             |
| 80 | 77, 79 | mpbid 222 |
. . . 4
         
      |
| 81 | | prmnn 15388 |
. . . . . . . 8
    
     |
| 82 | 4, 81 | syl 17 |
. . . . . . 7
        |
| 83 | 82, 5 | nnexpcld 13030 |
. . . . . 6
            |
| 84 | 83 | nnzd 11481 |
. . . . 5
            |
| 85 | | dvdsle 15032 |
. . . . 5
                                      
       |
| 86 | 84, 67, 85 | syl2anc 693 |
. . . 4
                      
       |
| 87 | 80, 86 | mpd 15 |
. . 3
         
      |
| 88 | | hashcl 13147 |
. . . . . 6
              |
| 89 | 64, 88 | syl 17 |
. . . . 5
            |
| 90 | 89 | nn0red 11352 |
. . . 4
            |
| 91 | 83 | nnred 11035 |
. . . 4
            |
| 92 | 90, 91 | letri3d 10179 |
. . 3
                
            
              |
| 93 | 16, 87, 92 | mpbir2and 957 |
. 2
                |
| 94 | | fveq2 6191 |
. . . 4
                  |
| 95 | 94 | eqeq1d 2624 |
. . 3
                  
             |
| 96 | 95 | rspcev 3309 |
. 2
      SubGrp SubGrp                     SubGrp SubGrp               |
| 97 | 14, 93, 96 | syl2anc 693 |
1
        SubGrp SubGrp               |