| Step | Hyp | Ref
| Expression |
|---|
| 1 | | cvxpconn.1 |
. . 3
     
  |
| 2 | | cvxpconn.2 |
. . 3
    
   
   
     ![[,] [,]](_icc.gif)                          |
| 3 | | cvxpconn.3 |
. . 3
      ℂfld ℂfld |
| 4 | | cvxpconn.4 |
. . 3
     ↾t
↾t   |
| 5 | 1, 2, 3, 4 | cvxpconn 31224 |
. 2
      PConn PConn |
| 6 | | simprl 794 |
. . . . 5
    
        
                      |
| 7 | | pconntop 31207 |
. . . . . . . . . 10
    PConn PConn      |
| 8 | 5, 7 | syl 17 |
. . . . . . . . 9
        |
| 9 | 8 | adantr 481 |
. . . . . . . 8
    
        
               
  |
| 10 | | eqid 2622 |
. . . . . . . . 9
      |
| 11 | 10 | toptopon 20722 |
. . . . . . . 8
     
   TopOn TopOn     |
| 12 | 9, 11 | sylib 208 |
. . . . . . 7
    
        
               
 TopOn TopOn     |
| 13 | | iiuni 22684 |
. . . . . . . . . 10
   ![[,] [,]](_icc.gif)      |
| 14 | 13, 10 | cnf 21050 |
. . . . . . . . 9
              ![[,] [,]](_icc.gif)       |
| 15 | 6, 14 | syl 17 |
. . . . . . . 8
    
        
                  ![[,] [,]](_icc.gif)       |
| 16 | | 0elunit 12290 |
. . . . . . . 8
     ![[,] [,]](_icc.gif)   |
| 17 | | ffvelrn 6357 |
. . . . . . . 8
       ![[,] [,]](_icc.gif)           ![[,] [,]](_icc.gif)              |
| 18 | 15, 16, 17 | sylancl 694 |
. . . . . . 7
    
        
                       |
| 19 | | eqid 2622 |
. . . . . . . 8
    ![[,] [,]](_icc.gif)                ![[,] [,]](_icc.gif)            |
| 20 | 19 | pcoptcl 22821 |
. . . . . . 7
      TopOn TopOn                   ![[,] [,]](_icc.gif)                       ![[,] [,]](_icc.gif)                          ![[,] [,]](_icc.gif)                       |
| 21 | 12, 18, 20 | syl2anc 693 |
. . . . . 6
    
        
                  ![[,] [,]](_icc.gif)                       ![[,] [,]](_icc.gif)                          ![[,] [,]](_icc.gif)                       |
| 22 | 21 | simp1d 1073 |
. . . . 5
    
        
                 ![[,] [,]](_icc.gif)                   |
| 23 | | iitopon 22682 |
. . . . . . . . . . 11
    TopOn TopOn   ![[,] [,]](_icc.gif)    |
| 24 | 23 | a1i 11 |
. . . . . . . . . 10
    
        
                 TopOn TopOn   ![[,] [,]](_icc.gif)     |
| 25 | 3 | dfii3 22686 |
. . . . . . . . . . . 12
     ↾t
↾t   ![[,] [,]](_icc.gif)    |
| 26 | 3 | cnfldtopon 22586 |
. . . . . . . . . . . . 13
    TopOn TopOn   |
| 27 | 26 | a1i 11 |
. . . . . . . . . . . 12
    
        
               
 TopOn TopOn    |
| 28 | | unitssre 12319 |
. . . . . . . . . . . . . 14
   ![[,] [,]](_icc.gif)     |
| 29 | | ax-resscn 9993 |
. . . . . . . . . . . . . 14
    |
| 30 | 28, 29 | sstri 3612 |
. . . . . . . . . . . . 13
   ![[,] [,]](_icc.gif)     |
| 31 | 30 | a1i 11 |
. . . . . . . . . . . 12
    
        
                ![[,] [,]](_icc.gif)   
  |
| 32 | 27, 27 | cnmpt2nd 21472 |
. . . . . . . . . . . 12
    
        
                   
                |
| 33 | 25, 27, 31, 25, 27, 31, 32 | cnmpt2res 21480 |
. . . . . . . . . . 11
    
        
                   ![[,] [,]](_icc.gif)        ![[,] [,]](_icc.gif)                 |
| 34 | 1 | adantr 481 |
. . . . . . . . . . . . 13
    
        
                  |
| 35 | | resttopon 20965 |
. . . . . . . . . . . . . . . . . 18
      TopOn TopOn  
    
   ↾t ↾t     TopOn TopOn    |
| 36 | 26, 1, 35 | sylancr 695 |
. . . . . . . . . . . . . . . . 17
      ↾t
↾t     TopOn TopOn    |
| 37 | 4, 36 | syl5eqel 2705 |
. . . . . . . . . . . . . . . 16
       TopOn TopOn    |
| 38 | | toponuni 20719 |
. . . . . . . . . . . . . . . 16
     TopOn TopOn   
     |
| 39 | 37, 38 | syl 17 |
. . . . . . . . . . . . . . 15
         |
| 40 | 39 | adantr 481 |
. . . . . . . . . . . . . 14
    
        
               
   |
| 41 | 18, 40 | eleqtrrd 2704 |
. . . . . . . . . . . . 13
    
        
                      |
| 42 | 34, 41 | sseldd 3604 |
. . . . . . . . . . . 12
    
        
                      |
| 43 | 24, 24, 27, 42 | cnmpt2c 21473 |
. . . . . . . . . . 11
    
        
                   ![[,] [,]](_icc.gif)        ![[,] [,]](_icc.gif)                     |
| 44 | 3 | mulcn 22670 |
. . . . . . . . . . . 12
            |
| 45 | 44 | a1i 11 |
. . . . . . . . . . 11
    
        
                          |
| 46 | 24, 24, 33, 43, 45 | cnmpt22f 21478 |
. . . . . . . . . 10
    
        
                   ![[,] [,]](_icc.gif)        ![[,] [,]](_icc.gif)                         |
| 47 | | ax-1cn 9994 |
. . . . . . . . . . . . . . 15
    |
| 48 | 47 | a1i 11 |
. . . . . . . . . . . . . 14
    
        
                  |
| 49 | 27, 27, 27, 48 | cnmpt2c 21473 |
. . . . . . . . . . . . 13
    
        
                   
                |
| 50 | 3 | subcn 22669 |
. . . . . . . . . . . . . 14
            |
| 51 | 50 | a1i 11 |
. . . . . . . . . . . . 13
    
        
               
          |
| 52 | 27, 27, 49, 32, 51 | cnmpt22f 21478 |
. . . . . . . . . . . 12
    
        
                   
                    |
| 53 | 25, 27, 31, 25, 27, 31, 52 | cnmpt2res 21480 |
. . . . . . . . . . 11
    
        
                   ![[,] [,]](_icc.gif)        ![[,] [,]](_icc.gif)                     |
| 54 | 24, 24 | cnmpt1st 21471 |
. . . . . . . . . . . 12
    
        
                   ![[,] [,]](_icc.gif)        ![[,] [,]](_icc.gif)                 |
| 55 | 3 | cnfldtop 22587 |
. . . . . . . . . . . . . 14
    |
| 56 | | cnrest2r 21091 |
. . . . . . . . . . . . . 14
        
  ↾t ↾t       
   |
| 57 | 55, 56 | ax-mp 5 |
. . . . . . . . . . . . 13
      ↾t ↾t    
     |
| 58 | 4 | oveq2i 6661 |
. . . . . . . . . . . . . 14
            ↾t ↾t    |
| 59 | 6, 58 | syl6eleq 2711 |
. . . . . . . . . . . . 13
    
        
                     ↾t ↾t     |
| 60 | 57, 59 | sseldi 3601 |
. . . . . . . . . . . 12
    
        
                      |
| 61 | 24, 24, 54, 60 | cnmpt21f 21475 |
. . . . . . . . . . 11
    
        
                   ![[,] [,]](_icc.gif)        ![[,] [,]](_icc.gif)                     |
| 62 | 24, 24, 53, 61, 45 | cnmpt22f 21478 |
. . . . . . . . . 10
    
        
                   ![[,] [,]](_icc.gif)        ![[,] [,]](_icc.gif)                             |
| 63 | 3 | addcn 22668 |
. . . . . . . . . . 11
            |
| 64 | 63 | a1i 11 |
. . . . . . . . . 10
    
        
               
          |
| 65 | 24, 24, 46, 62, 64 | cnmpt22f 21478 |
. . . . . . . . 9
    
        
                   ![[,] [,]](_icc.gif)        ![[,] [,]](_icc.gif)                                         |
| 66 | 41 | adantr 481 |
. . . . . . . . . . . . . 14
                                  ![[,] [,]](_icc.gif)        ![[,] [,]](_icc.gif)              |
| 67 | 15 | adantr 481 |
. . . . . . . . . . . . . . . 16
                                  ![[,] [,]](_icc.gif)        ![[,] [,]](_icc.gif)          ![[,] [,]](_icc.gif)       |
| 68 | | simprl 794 |
. . . . . . . . . . . . . . . 16
                                  ![[,] [,]](_icc.gif)        ![[,] [,]](_icc.gif)          ![[,] [,]](_icc.gif)    |
| 69 | 67, 68 | ffvelrnd 6360 |
. . . . . . . . . . . . . . 15
                                  ![[,] [,]](_icc.gif)        ![[,] [,]](_icc.gif)               |
| 70 | 40 | adantr 481 |
. . . . . . . . . . . . . . 15
                                  ![[,] [,]](_icc.gif)        ![[,] [,]](_icc.gif)       
   |
| 71 | 69, 70 | eleqtrrd 2704 |
. . . . . . . . . . . . . 14
                                  ![[,] [,]](_icc.gif)        ![[,] [,]](_icc.gif)              |
| 72 | 2 | 3exp2 1285 |
. . . . . . . . . . . . . . . . . 18
                   ![[,] [,]](_icc.gif)                           |
| 73 | 72 | imp42 620 |
. . . . . . . . . . . . . . . . 17
            
   
    ![[,] [,]](_icc.gif)                         |
| 74 | 73 | an32s 846 |
. . . . . . . . . . . . . . . 16
          ![[,] [,]](_icc.gif)           
   
                    |
| 75 | 74 | ralrimivva 2971 |
. . . . . . . . . . . . . . 15
    
    ![[,] [,]](_icc.gif)        
   
                    |
| 76 | 75 | ad2ant2rl 785 |
. . . . . . . . . . . . . 14
                                  ![[,] [,]](_icc.gif)        ![[,] [,]](_icc.gif)       
   
                      |
| 77 | | oveq2 6658 |
. . . . . . . . . . . . . . . . 17
                          |
| 78 | 77 | oveq1d 6665 |
. . . . . . . . . . . . . . . 16
                                                  |
| 79 | 78 | eleq1d 2686 |
. . . . . . . . . . . . . . 15
                              
                         |
| 80 | | oveq2 6658 |
. . . . . . . . . . . . . . . . 17
                                  |
| 81 | 80 | oveq2d 6666 |
. . . . . . . . . . . . . . . 16
                                                          |
| 82 | 81 | eleq1d 2686 |
. . . . . . . . . . . . . . 15
                                  
                             |
| 83 | 79, 82 | rspc2va 3323 |
. . . . . . . . . . . . . 14
                                                 
                            |
| 84 | 66, 71, 76, 83 | syl21anc 1325 |
. . . . . . . . . . . . 13
                                  ![[,] [,]](_icc.gif)        ![[,] [,]](_icc.gif)                                  |
| 85 | 84 | ralrimivva 2971 |
. . . . . . . . . . . 12
    
        
               
   ![[,] [,]](_icc.gif)        ![[,] [,]](_icc.gif)                               |
| 86 | | eqid 2622 |
. . . . . . . . . . . . 13
      ![[,] [,]](_icc.gif)        ![[,] [,]](_icc.gif)                                    ![[,] [,]](_icc.gif)        ![[,] [,]](_icc.gif)                              |
| 87 | 86 | fmpt2 7237 |
. . . . . . . . . . . 12
    
  ![[,] [,]](_icc.gif)     
  ![[,] [,]](_icc.gif)                              
     ![[,] [,]](_icc.gif)        ![[,] [,]](_icc.gif)                                  ![[,] [,]](_icc.gif)      ![[,] [,]](_icc.gif)       |
| 88 | 85, 87 | sylib 208 |
. . . . . . . . . . 11
    
        
                   ![[,] [,]](_icc.gif)        ![[,] [,]](_icc.gif)                                  ![[,] [,]](_icc.gif)      ![[,] [,]](_icc.gif)       |
| 89 | | frn 6053 |
. . . . . . . . . . 11
       ![[,] [,]](_icc.gif)        ![[,] [,]](_icc.gif)                                  ![[,] [,]](_icc.gif)      ![[,] [,]](_icc.gif)       
     ![[,] [,]](_icc.gif)        ![[,] [,]](_icc.gif)                                 |
| 90 | 88, 89 | syl 17 |
. . . . . . . . . 10
    
        
                    ![[,] [,]](_icc.gif)        ![[,] [,]](_icc.gif)                                 |
| 91 | | cnrest2 21090 |
. . . . . . . . . 10
      TopOn TopOn  
       ![[,] [,]](_icc.gif)        ![[,] [,]](_icc.gif)                              
             ![[,] [,]](_icc.gif)        ![[,] [,]](_icc.gif)                                    
         ![[,] [,]](_icc.gif)        ![[,] [,]](_icc.gif)                                    
   ↾t ↾t      |
| 92 | 27, 90, 34, 91 | syl3anc 1326 |
. . . . . . . . 9
    
        
                    ![[,] [,]](_icc.gif)        ![[,] [,]](_icc.gif)                                    
         ![[,] [,]](_icc.gif)        ![[,] [,]](_icc.gif)                                    
   ↾t ↾t      |
| 93 | 65, 92 | mpbid 222 |
. . . . . . . 8
    
        
                   ![[,] [,]](_icc.gif)        ![[,] [,]](_icc.gif)                                        ↾t ↾t     |
| 94 | 4 | oveq2i 6661 |
. . . . . . . 8
    
               ↾t ↾t    |
| 95 | 93, 94 | syl6eleqr 2712 |
. . . . . . 7
    
        
                   ![[,] [,]](_icc.gif)        ![[,] [,]](_icc.gif)                                         |
| 96 | | simpr 477 |
. . . . . . . . 9
                                 ![[,] [,]](_icc.gif)         ![[,] [,]](_icc.gif)    |
| 97 | | simpr 477 |
. . . . . . . . . . . 12
        
       |
| 98 | 97 | oveq1d 6665 |
. . . . . . . . . . 11
        
                       |
| 99 | 97 | oveq2d 6666 |
. . . . . . . . . . . . 13
        
               |
| 100 | | 1m0e1 11131 |
. . . . . . . . . . . . 13
        |
| 101 | 99, 100 | syl6eq 2672 |
. . . . . . . . . . . 12
        
           |
| 102 | | simpl 473 |
. . . . . . . . . . . . 13
        
       |
| 103 | 102 | fveq2d 6195 |
. . . . . . . . . . . 12
        
               |
| 104 | 101, 103 | oveq12d 6668 |
. . . . . . . . . . 11
        
                           |
| 105 | 98, 104 | oveq12d 6668 |
. . . . . . . . . 10
        
                                                   |
| 106 | | ovex 6678 |
. . . . . . . . . 10
                        |
| 107 | 105, 86, 106 | ovmpt2a 6791 |
. . . . . . . . 9
       ![[,] [,]](_icc.gif)     
  ![[,] [,]](_icc.gif)            ![[,] [,]](_icc.gif)        ![[,] [,]](_icc.gif)                                                       |
| 108 | 96, 16, 107 | sylancl 694 |
. . . . . . . 8
                                 ![[,] [,]](_icc.gif)            ![[,] [,]](_icc.gif)        ![[,] [,]](_icc.gif)                                                       |
| 109 | 42 | adantr 481 |
. . . . . . . . . 10
                                 ![[,] [,]](_icc.gif)             |
| 110 | 109 | mul02d 10234 |
. . . . . . . . 9
                                 ![[,] [,]](_icc.gif)                 |
| 111 | 26 | toponunii 20721 |
. . . . . . . . . . . . 13
     |
| 112 | 13, 111 | cnf 21050 |
. . . . . . . . . . . 12
              ![[,] [,]](_icc.gif)      |
| 113 | 60, 112 | syl 17 |
. . . . . . . . . . 11
    
        
                  ![[,] [,]](_icc.gif)      |
| 114 | 113 | ffvelrnda 6359 |
. . . . . . . . . 10
                                 ![[,] [,]](_icc.gif)             |
| 115 | 114 | mulid2d 10058 |
. . . . . . . . 9
                                 ![[,] [,]](_icc.gif)                     |
| 116 | 110, 115 | oveq12d 6668 |
. . . . . . . 8
                                 ![[,] [,]](_icc.gif)                                     |
| 117 | 114 | addid2d 10237 |
. . . . . . . 8
                                 ![[,] [,]](_icc.gif)                     |
| 118 | 108, 116,
117 | 3eqtrd 2660 |
. . . . . . 7
                                 ![[,] [,]](_icc.gif)            ![[,] [,]](_icc.gif)        ![[,] [,]](_icc.gif)                                       |
| 119 | | 1elunit 12291 |
. . . . . . . . 9
     ![[,] [,]](_icc.gif)   |
| 120 | | simpr 477 |
. . . . . . . . . . . 12
        
       |
| 121 | 120 | oveq1d 6665 |
. . . . . . . . . . 11
        
                       |
| 122 | 120 | oveq2d 6666 |
. . . . . . . . . . . . 13
        
               |
| 123 | | 1m1e0 11089 |
. . . . . . . . . . . . 13
        |
| 124 | 122, 123 | syl6eq 2672 |
. . . . . . . . . . . 12
        
           |
| 125 | | simpl 473 |
. . . . . . . . . . . . 13
        
       |
| 126 | 125 | fveq2d 6195 |
. . . . . . . . . . . 12
        
               |
| 127 | 124, 126 | oveq12d 6668 |
. . . . . . . . . . 11
        
                           |
| 128 | 121, 127 | oveq12d 6668 |
. . . . . . . . . 10
        
                                                   |
| 129 | | ovex 6678 |
. . . . . . . . . 10
                        |
| 130 | 128, 86, 129 | ovmpt2a 6791 |
. . . . . . . . 9
       ![[,] [,]](_icc.gif)     
  ![[,] [,]](_icc.gif)            ![[,] [,]](_icc.gif)        ![[,] [,]](_icc.gif)                                                       |
| 131 | 96, 119, 130 | sylancl 694 |
. . . . . . . 8
                                 ![[,] [,]](_icc.gif)            ![[,] [,]](_icc.gif)        ![[,] [,]](_icc.gif)                                                       |
| 132 | 109 | mulid2d 10058 |
. . . . . . . . 9
                                 ![[,] [,]](_icc.gif)                     |
| 133 | 114 | mul02d 10234 |
. . . . . . . . 9
                                 ![[,] [,]](_icc.gif)                 |
| 134 | 132, 133 | oveq12d 6668 |
. . . . . . . 8
                                 ![[,] [,]](_icc.gif)                                     |
| 135 | 109 | addid1d 10236 |
. . . . . . . . 9
                                 ![[,] [,]](_icc.gif)                     |
| 136 | | fvex 6201 |
. . . . . . . . . . 11
        |
| 137 | 136 | fvconst2 6469 |
. . . . . . . . . 10
      ![[,] [,]](_icc.gif)        ![[,] [,]](_icc.gif)                      |
| 138 | 137 | adantl 482 |
. . . . . . . . 9
                                 ![[,] [,]](_icc.gif)         ![[,] [,]](_icc.gif)                      |
| 139 | 135, 138 | eqtr4d 2659 |
. . . . . . . 8
                                 ![[,] [,]](_icc.gif)                   ![[,] [,]](_icc.gif)                |
| 140 | 131, 134,
139 | 3eqtrd 2660 |
. . . . . . 7
                                 ![[,] [,]](_icc.gif)            ![[,] [,]](_icc.gif)        ![[,] [,]](_icc.gif)                                     ![[,] [,]](_icc.gif)                |
| 141 | | simpr 477 |
. . . . . . . . . . . 12
                |
| 142 | 141 | oveq1d 6665 |
. . . . . . . . . . 11
                                |
| 143 | 141 | oveq2d 6666 |
. . . . . . . . . . . 12
                        |
| 144 | | simpl 473 |
. . . . . . . . . . . . 13
                |
| 145 | 144 | fveq2d 6195 |
. . . . . . . . . . . 12
                        |
| 146 | 143, 145 | oveq12d 6668 |
. . . . . . . . . . 11
                                        |
| 147 | 142, 146 | oveq12d 6668 |
. . . . . . . . . 10
                                                                |
| 148 | | ovex 6678 |
. . . . . . . . . 10
                            |
| 149 | 147, 86, 148 | ovmpt2a 6791 |
. . . . . . . . 9
       ![[,] [,]](_icc.gif)     
  ![[,] [,]](_icc.gif)            ![[,] [,]](_icc.gif)        ![[,] [,]](_icc.gif)                                                           |
| 150 | 16, 96, 149 | sylancr 695 |
. . . . . . . 8
                                 ![[,] [,]](_icc.gif)            ![[,] [,]](_icc.gif)        ![[,] [,]](_icc.gif)                                                           |
| 151 | 30, 96 | sseldi 3601 |
. . . . . . . . . . 11
                                 ![[,] [,]](_icc.gif)         |
| 152 | | pncan3 10289 |
. . . . . . . . . . 11
        
               |
| 153 | 151, 47, 152 | sylancl 694 |
. . . . . . . . . 10
                                 ![[,] [,]](_icc.gif)                 |
| 154 | 153 | oveq1d 6665 |
. . . . . . . . 9
                                 ![[,] [,]](_icc.gif)                                 |
| 155 | | subcl 10280 |
. . . . . . . . . . 11
        
           |
| 156 | 47, 151, 155 | sylancr 695 |
. . . . . . . . . 10
                                 ![[,] [,]](_icc.gif)             |
| 157 | 151, 156,
109 | adddird 10065 |
. . . . . . . . 9
                                 ![[,] [,]](_icc.gif)                                                 |
| 158 | 154, 157,
132 | 3eqtr3d 2664 |
. . . . . . . 8
                                 ![[,] [,]](_icc.gif)                                     |
| 159 | 150, 158 | eqtrd 2656 |
. . . . . . 7
                                 ![[,] [,]](_icc.gif)            ![[,] [,]](_icc.gif)        ![[,] [,]](_icc.gif)                                       |
| 160 | | simpr 477 |
. . . . . . . . . . . 12
                |
| 161 | 160 | oveq1d 6665 |
. . . . . . . . . . 11
                                |
| 162 | 160 | oveq2d 6666 |
. . . . . . . . . . . 12
                        |
| 163 | | simpl 473 |
. . . . . . . . . . . . 13
                |
| 164 | 163 | fveq2d 6195 |
. . . . . . . . . . . 12
                        |
| 165 | 162, 164 | oveq12d 6668 |
. . . . . . . . . . 11
                                        |
| 166 | 161, 165 | oveq12d 6668 |
. . . . . . . . . 10
                                                                |
| 167 | | ovex 6678 |
. . . . . . . . . 10
                            |
| 168 | 166, 86, 167 | ovmpt2a 6791 |
. . . . . . . . 9
       ![[,] [,]](_icc.gif)     
  ![[,] [,]](_icc.gif)            ![[,] [,]](_icc.gif)        ![[,] [,]](_icc.gif)                                                           |
| 169 | 119, 96, 168 | sylancr 695 |
. . . . . . . 8
                                 ![[,] [,]](_icc.gif)            ![[,] [,]](_icc.gif)        ![[,] [,]](_icc.gif)                                                           |
| 170 | | simplrr 801 |
. . . . . . . . . . 11
                                 ![[,] [,]](_icc.gif)                 |
| 171 | 170 | oveq2d 6666 |
. . . . . . . . . 10
                                 ![[,] [,]](_icc.gif)                                 |
| 172 | 171 | oveq2d 6666 |
. . . . . . . . 9
                                 ![[,] [,]](_icc.gif)                                                         |
| 173 | 158, 172,
170 | 3eqtr3d 2664 |
. . . . . . . 8
                                 ![[,] [,]](_icc.gif)                                     |
| 174 | 169, 173 | eqtrd 2656 |
. . . . . . 7
                                 ![[,] [,]](_icc.gif)            ![[,] [,]](_icc.gif)        ![[,] [,]](_icc.gif)                                       |
| 175 | 6, 22, 95, 118, 140, 159, 174 | isphtpy2d 22786 |
. . . . . 6
    
        
                   ![[,] [,]](_icc.gif)        ![[,] [,]](_icc.gif)                                  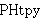       ![[,] [,]](_icc.gif)              |
| 176 | | ne0i 3921 |
. . . . . 6
       ![[,] [,]](_icc.gif)        ![[,] [,]](_icc.gif)                                  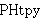       ![[,] [,]](_icc.gif)                 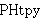       ![[,] [,]](_icc.gif)                |
| 177 | 175, 176 | syl 17 |
. . . . 5
    
        
                 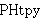       ![[,] [,]](_icc.gif)                |
| 178 | | isphtpc 22793 |
. . . . 5
    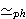
      ![[,] [,]](_icc.gif)            
        
   ![[,] [,]](_icc.gif)                      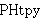       ![[,] [,]](_icc.gif)                 |
| 179 | 6, 22, 177, 178 | syl3anbrc 1246 |
. . . 4
    
        
                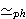       ![[,] [,]](_icc.gif)             |
| 180 | 179 | expr 643 |
. . 3
    
   
                    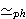       ![[,] [,]](_icc.gif)              |
| 181 | 180 | ralrimiva 2966 |
. 2
                           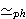       ![[,] [,]](_icc.gif)              |
| 182 | | issconn 31208 |
. 2
    SConn SConn     PConn PConn    
                    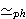       ![[,] [,]](_icc.gif)               |
| 183 | 5, 181, 182 | sylanbrc 698 |
1
      SConn SConn |