| Step | Hyp | Ref
| Expression |
|---|
| 1 | | sylow2a.y |
. . . . 5
        |
| 2 | | pwfi 8261 |
. . . . 5
     
     |
| 3 | 1, 2 | sylib 208 |
. . . 4
         |
| 4 | | sylow2a.m |
. . . . . 6
     
  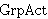    |
| 5 | | sylow2a.r |
. . . . . . 7
         
           
          |
| 6 | | sylow2a.x |
. . . . . . 7
        |
| 7 | 5, 6 | gaorber 17741 |
. . . . . 6
      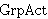    
   |
| 8 | 4, 7 | syl 17 |
. . . . 5
        |
| 9 | 8 | qsss 7808 |
. . . 4
             |
| 10 | | ssfi 8180 |
. . . 4
                          |
| 11 | 3, 9, 10 | syl2anc 693 |
. . 3
         
  |
| 12 | | diffi 8192 |
. . 3
         
             |
| 13 | 11, 12 | syl 17 |
. 2
                 |
| 14 | | sylow2a.p |
. . . . 5
     pGrp pGrp   |
| 15 | | gagrp 17725 |
. . . . . . 7
      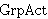        |
| 16 | 4, 15 | syl 17 |
. . . . . 6
        |
| 17 | | sylow2a.f |
. . . . . 6
        |
| 18 | 6 | pgpfi 18020 |
. . . . . 6
        
     pGrp pGrp  
    
                  |
| 19 | 16, 17, 18 | syl2anc 693 |
. . . . 5
      pGrp pGrp  
    
                  |
| 20 | 14, 19 | mpbid 222 |
. . . 4
                          |
| 21 | 20 | simpld 475 |
. . 3
        |
| 22 | | prmz 15389 |
. . 3
    
     |
| 23 | 21, 22 | syl 17 |
. 2
        |
| 24 | | eldifi 3732 |
. . . . 5
                       |
| 25 | 1 | adantr 481 |
. . . . . 6
    
        
    |
| 26 | 9 | sselda 3603 |
. . . . . . 7
    
        
     |
| 27 | 26 | elpwid 4170 |
. . . . . 6
    
        
    |
| 28 | | ssfi 8180 |
. . . . . 6
                |
| 29 | 25, 27, 28 | syl2anc 693 |
. . . . 5
    
        
    |
| 30 | 24, 29 | sylan2 491 |
. . . 4
    
                  |
| 31 | | hashcl 13147 |
. . . 4
              |
| 32 | 30, 31 | syl 17 |
. . 3
    
                      |
| 33 | 32 | nn0zd 11480 |
. 2
    
                      |
| 34 | | eldif 3584 |
. . 3
              
                |
| 35 | | eqid 2622 |
. . . . 5
            |
| 36 | | sseq1 3626 |
. . . . . . . 8
    ![] ]](rbrack.gif)        ![] ]](rbrack.gif)  
 
     |
| 37 | | selpw 4165 |
. . . . . . . 8
      
    |
| 38 | 36, 37 | syl6bbr 278 |
. . . . . . 7
    ![] ]](rbrack.gif)        ![] ]](rbrack.gif)  
 
      |
| 39 | 38 | notbid 308 |
. . . . . 6
    ![] ]](rbrack.gif)         ![] ]](rbrack.gif)            |
| 40 | | fveq2 6191 |
. . . . . . 7
    ![] ]](rbrack.gif)          ![] ]](rbrack.gif)          |
| 41 | 40 | breq2d 4665 |
. . . . . 6
    ![] ]](rbrack.gif)             ![] ]](rbrack.gif)   
         |
| 42 | 39, 41 | imbi12d 334 |
. . . . 5
    ![] ]](rbrack.gif)          ![] ]](rbrack.gif)    
       ![] ]](rbrack.gif)    
   
             |
| 43 | 21 | adantr 481 |
. . . . . . . . . 10
    
         |
| 44 | 8 | adantr 481 |
. . . . . . . . . . . . . 14
    
         |
| 45 | | simpr 477 |
. . . . . . . . . . . . . 14
    
         |
| 46 | 44, 45 | erref 7762 |
. . . . . . . . . . . . 13
    
         |
| 47 | | vex 3203 |
. . . . . . . . . . . . . 14
    |
| 48 | 47, 47 | elec 7786 |
. . . . . . . . . . . . 13
      ![] ]](rbrack.gif)       |
| 49 | 46, 48 | sylibr 224 |
. . . . . . . . . . . 12
    
         ![] ]](rbrack.gif)   |
| 50 | | ne0i 3921 |
. . . . . . . . . . . 12
      ![] ]](rbrack.gif)     ![] ]](rbrack.gif)     |
| 51 | 49, 50 | syl 17 |
. . . . . . . . . . 11
    
       ![] ]](rbrack.gif)     |
| 52 | 8 | ecss 7788 |
. . . . . . . . . . . . . 14
      ![] ]](rbrack.gif)     |
| 53 | | ssfi 8180 |
. . . . . . . . . . . . . 14
         ![] ]](rbrack.gif)     
  ![] ]](rbrack.gif)     |
| 54 | 1, 52, 53 | syl2anc 693 |
. . . . . . . . . . . . 13
      ![] ]](rbrack.gif)     |
| 55 | 54 | adantr 481 |
. . . . . . . . . . . 12
    
       ![] ]](rbrack.gif)     |
| 56 | | hashnncl 13157 |
. . . . . . . . . . . 12
    ![] ]](rbrack.gif)           ![] ]](rbrack.gif)   
 
  ![] ]](rbrack.gif)      |
| 57 | 55, 56 | syl 17 |
. . . . . . . . . . 11
    
           ![] ]](rbrack.gif)        ![] ]](rbrack.gif)      |
| 58 | 51, 57 | mpbird 247 |
. . . . . . . . . 10
    
          ![] ]](rbrack.gif)  
   |
| 59 | | pceq0 15575 |
. . . . . . . . . 10
            ![] ]](rbrack.gif)  
             ![] ]](rbrack.gif)               ![] ]](rbrack.gif)     |
| 60 | 43, 58, 59 | syl2anc 693 |
. . . . . . . . 9
    
              ![] ]](rbrack.gif)        
      ![] ]](rbrack.gif)     |
| 61 | | oveq2 6658 |
. . . . . . . . . 10
    
     ![] ]](rbrack.gif)                  ![] ]](rbrack.gif)            |
| 62 | | hashcl 13147 |
. . . . . . . . . . . . . . . . . . . . . 22
    ![] ]](rbrack.gif)          ![] ]](rbrack.gif)      |
| 63 | 54, 62 | syl 17 |
. . . . . . . . . . . . . . . . . . . . 21
         ![] ]](rbrack.gif)      |
| 64 | 63 | nn0zd 11480 |
. . . . . . . . . . . . . . . . . . . 20
         ![] ]](rbrack.gif)      |
| 65 | | ssrab2 3687 |
. . . . . . . . . . . . . . . . . . . . . . 23
        
       |
| 66 | | ssfi 8180 |
. . . . . . . . . . . . . . . . . . . . . . 23
                               
        |
| 67 | 17, 65, 66 | sylancl 694 |
. . . . . . . . . . . . . . . . . . . . . 22
                    |
| 68 | | hashcl 13147 |
. . . . . . . . . . . . . . . . . . . . . 22
                                      |
| 69 | 67, 68 | syl 17 |
. . . . . . . . . . . . . . . . . . . . 21
                        |
| 70 | 69 | nn0zd 11480 |
. . . . . . . . . . . . . . . . . . . 20
                        |
| 71 | | dvdsmul1 15003 |
. . . . . . . . . . . . . . . . . . . 20
        ![] ]](rbrack.gif)                                ![] ]](rbrack.gif)          ![] ]](rbrack.gif)                       |
| 72 | 64, 70, 71 | syl2anc 693 |
. . . . . . . . . . . . . . . . . . 19
         ![] ]](rbrack.gif)          ![] ]](rbrack.gif)                       |
| 73 | 72 | adantr 481 |
. . . . . . . . . . . . . . . . . 18
    
          ![] ]](rbrack.gif)  
       ![] ]](rbrack.gif)                       |
| 74 | 4 | adantr 481 |
. . . . . . . . . . . . . . . . . . 19
    
         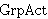    |
| 75 | 17 | adantr 481 |
. . . . . . . . . . . . . . . . . . 19
    
         |
| 76 | | eqid 2622 |
. . . . . . . . . . . . . . . . . . . 20
        
                   |
| 77 | | eqid 2622 |
. . . . . . . . . . . . . . . . . . . 20
   ~QG ~QG                  ~QG ~QG        
      |
| 78 | 6, 76, 77, 5 | orbsta2 17747 |
. . . . . . . . . . . . . . . . . . 19
    
   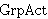     
   
                ![] ]](rbrack.gif)                       |
| 79 | 74, 45, 75, 78 | syl21anc 1325 |
. . . . . . . . . . . . . . . . . 18
    
                 ![] ]](rbrack.gif)                       |
| 80 | 73, 79 | breqtrrd 4681 |
. . . . . . . . . . . . . . . . 17
    
          ![] ]](rbrack.gif)  
       |
| 81 | 20 | simprd 479 |
. . . . . . . . . . . . . . . . . 18
                    |
| 82 | 81 | adantr 481 |
. . . . . . . . . . . . . . . . 17
    
                     |
| 83 | | breq2 4657 |
. . . . . . . . . . . . . . . . . . 19
                    ![] ]](rbrack.gif)         
     ![] ]](rbrack.gif)           |
| 84 | 83 | biimpcd 239 |
. . . . . . . . . . . . . . . . . 18
       ![] ]](rbrack.gif)                            ![] ]](rbrack.gif)           |
| 85 | 84 | reximdv 3016 |
. . . . . . . . . . . . . . . . 17
       ![] ]](rbrack.gif)                            
       ![] ]](rbrack.gif)           |
| 86 | 80, 82, 85 | sylc 65 |
. . . . . . . . . . . . . . . 16
    
              ![] ]](rbrack.gif)          |
| 87 | | pcprmpw2 15586 |
. . . . . . . . . . . . . . . . 17
            ![] ]](rbrack.gif)  
              ![] ]](rbrack.gif)               ![] ]](rbrack.gif)               ![] ]](rbrack.gif)       |
| 88 | 43, 58, 87 | syl2anc 693 |
. . . . . . . . . . . . . . . 16
    
       
       ![] ]](rbrack.gif)         
     ![] ]](rbrack.gif)               ![] ]](rbrack.gif)       |
| 89 | 86, 88 | mpbid 222 |
. . . . . . . . . . . . . . 15
    
          ![] ]](rbrack.gif)  
            ![] ]](rbrack.gif)      |
| 90 | 89 | eqcomd 2628 |
. . . . . . . . . . . . . 14
    
                ![] ]](rbrack.gif)           ![] ]](rbrack.gif)    |
| 91 | 23 | adantr 481 |
. . . . . . . . . . . . . . . . 17
    
         |
| 92 | 91 | zcnd 11483 |
. . . . . . . . . . . . . . . 16
    
         |
| 93 | 92 | exp0d 13002 |
. . . . . . . . . . . . . . 15
    
             |
| 94 | | hash1 13192 |
. . . . . . . . . . . . . . 15
        |
| 95 | 93, 94 | syl6eqr 2674 |
. . . . . . . . . . . . . 14
    
                 |
| 96 | 90, 95 | eqeq12d 2637 |
. . . . . . . . . . . . 13
    
                 ![] ]](rbrack.gif)                 ![] ]](rbrack.gif)           |
| 97 | | df1o2 7572 |
. . . . . . . . . . . . . . 15
      |
| 98 | | snfi 8038 |
. . . . . . . . . . . . . . 15
      |
| 99 | 97, 98 | eqeltri 2697 |
. . . . . . . . . . . . . 14
    |
| 100 | | hashen 13135 |
. . . . . . . . . . . . . 14
     ![] ]](rbrack.gif)        
       ![] ]](rbrack.gif)            ![] ]](rbrack.gif)      |
| 101 | 55, 99, 100 | sylancl 694 |
. . . . . . . . . . . . 13
    
           ![] ]](rbrack.gif)            ![] ]](rbrack.gif)      |
| 102 | 96, 101 | bitrd 268 |
. . . . . . . . . . . 12
    
                 ![] ]](rbrack.gif)              ![] ]](rbrack.gif)      |
| 103 | | en1b 8024 |
. . . . . . . . . . . 12
    ![] ]](rbrack.gif)       ![] ]](rbrack.gif)       ![] ]](rbrack.gif)    |
| 104 | 102, 103 | syl6bb 276 |
. . . . . . . . . . 11
    
                 ![] ]](rbrack.gif)              ![] ]](rbrack.gif)       ![] ]](rbrack.gif)     |
| 105 | 45 | adantr 481 |
. . . . . . . . . . . . . . . . . 18
                  ![] ]](rbrack.gif)       ![] ]](rbrack.gif)       
  |
| 106 | 4 | ad2antrr 762 |
. . . . . . . . . . . . . . . . . . . 20
                  ![] ]](rbrack.gif)       ![] ]](rbrack.gif)          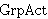    |
| 107 | 6 | gaf 17728 |
. . . . . . . . . . . . . . . . . . . 20
      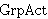              |
| 108 | 106, 107 | syl 17 |
. . . . . . . . . . . . . . . . . . 19
                  ![] ]](rbrack.gif)       ![] ]](rbrack.gif)                |
| 109 | | simprl 794 |
. . . . . . . . . . . . . . . . . . 19
                  ![] ]](rbrack.gif)       ![] ]](rbrack.gif)       
  |
| 110 | 108, 109,
105 | fovrnd 6806 |
. . . . . . . . . . . . . . . . . 18
                  ![] ]](rbrack.gif)       ![] ]](rbrack.gif)              |
| 111 | | eqid 2622 |
. . . . . . . . . . . . . . . . . . 19
         
  |
| 112 | | oveq1 6657 |
. . . . . . . . . . . . . . . . . . . . 21
                  |
| 113 | 112 | eqeq1d 2624 |
. . . . . . . . . . . . . . . . . . . 20
                                |
| 114 | 113 | rspcev 3309 |
. . . . . . . . . . . . . . . . . . 19
        
              
        
   |
| 115 | 109, 111,
114 | sylancl 694 |
. . . . . . . . . . . . . . . . . 18
                  ![] ]](rbrack.gif)       ![] ]](rbrack.gif)       
              |
| 116 | 5 | gaorb 17740 |
. . . . . . . . . . . . . . . . . 18
                                        |
| 117 | 105, 110,
115, 116 | syl3anbrc 1246 |
. . . . . . . . . . . . . . . . 17
                  ![] ]](rbrack.gif)       ![] ]](rbrack.gif)              |
| 118 | | ovex 6678 |
. . . . . . . . . . . . . . . . . 18
        |
| 119 | 118, 47 | elec 7786 |
. . . . . . . . . . . . . . . . 17
    
     ![] ]](rbrack.gif)           |
| 120 | 117, 119 | sylibr 224 |
. . . . . . . . . . . . . . . 16
                  ![] ]](rbrack.gif)       ![] ]](rbrack.gif)              ![] ]](rbrack.gif)   |
| 121 | | simprr 796 |
. . . . . . . . . . . . . . . 16
                  ![] ]](rbrack.gif)       ![] ]](rbrack.gif)        ![] ]](rbrack.gif)       ![] ]](rbrack.gif)    |
| 122 | 120, 121 | eleqtrd 2703 |
. . . . . . . . . . . . . . 15
                  ![] ]](rbrack.gif)       ![] ]](rbrack.gif)                ![] ]](rbrack.gif)    |
| 123 | 118 | elsn 4192 |
. . . . . . . . . . . . . . 15
    
       ![] ]](rbrack.gif)   
         ![] ]](rbrack.gif)   |
| 124 | 122, 123 | sylib 208 |
. . . . . . . . . . . . . 14
                  ![] ]](rbrack.gif)       ![] ]](rbrack.gif)               ![] ]](rbrack.gif)   |
| 125 | 49 | adantr 481 |
. . . . . . . . . . . . . . . 16
                  ![] ]](rbrack.gif)       ![] ]](rbrack.gif)       
  ![] ]](rbrack.gif)   |
| 126 | 125, 121 | eleqtrd 2703 |
. . . . . . . . . . . . . . 15
                  ![] ]](rbrack.gif)       ![] ]](rbrack.gif)       
    ![] ]](rbrack.gif)    |
| 127 | 47 | elsn 4192 |
. . . . . . . . . . . . . . 15
        ![] ]](rbrack.gif)         ![] ]](rbrack.gif)   |
| 128 | 126, 127 | sylib 208 |
. . . . . . . . . . . . . 14
                  ![] ]](rbrack.gif)       ![] ]](rbrack.gif)       
   ![] ]](rbrack.gif)   |
| 129 | 124, 128 | eqtr4d 2659 |
. . . . . . . . . . . . 13
                  ![] ]](rbrack.gif)       ![] ]](rbrack.gif)              |
| 130 | 129 | expr 643 |
. . . . . . . . . . . 12
                   ![] ]](rbrack.gif)       ![] ]](rbrack.gif)             |
| 131 | 130 | ralrimdva 2969 |
. . . . . . . . . . 11
    
        ![] ]](rbrack.gif)       ![] ]](rbrack.gif)       
         |
| 132 | 104, 131 | sylbid 230 |
. . . . . . . . . 10
    
                 ![] ]](rbrack.gif)                 
       |
| 133 | 61, 132 | syl5 34 |
. . . . . . . . 9
    
              ![] ]](rbrack.gif)            
       |
| 134 | 60, 133 | sylbird 250 |
. . . . . . . 8
    
       
      ![] ]](rbrack.gif)         
       |
| 135 | | oveq2 6658 |
. . . . . . . . . . . . 13
                  |
| 136 | | id 22 |
. . . . . . . . . . . . 13
          |
| 137 | 135, 136 | eqeq12d 2637 |
. . . . . . . . . . . 12
              
         |
| 138 | 137 | ralbidv 2986 |
. . . . . . . . . . 11
        
   
     
   
         |
| 139 | | sylow2a.z |
. . . . . . . . . . 11
             
      |
| 140 | 138, 139 | elrab2 3366 |
. . . . . . . . . 10
     
   
    
         |
| 141 | 140 | baib 944 |
. . . . . . . . 9
          
   
         |
| 142 | 141 | adantl 482 |
. . . . . . . 8
    
         
   
         |
| 143 | 134, 142 | sylibrd 249 |
. . . . . . 7
    
       
      ![] ]](rbrack.gif)         |
| 144 | 6, 4, 14, 17, 1, 139, 5 | sylow2alem1 18032 |
. . . . . . . . . 10
    
       ![] ]](rbrack.gif)       |
| 145 | | simpr 477 |
. . . . . . . . . . 11
    
         |
| 146 | 145 | snssd 4340 |
. . . . . . . . . 10
    
           |
| 147 | 144, 146 | eqsstrd 3639 |
. . . . . . . . 9
    
       ![] ]](rbrack.gif)  
  |
| 148 | 147 | ex 450 |
. . . . . . . 8
           ![] ]](rbrack.gif)      |
| 149 | 148 | adantr 481 |
. . . . . . 7
    
            ![] ]](rbrack.gif)      |
| 150 | 143, 149 | syld 47 |
. . . . . 6
    
       
      ![] ]](rbrack.gif)      ![] ]](rbrack.gif)      |
| 151 | 150 | con1d 139 |
. . . . 5
    
         ![] ]](rbrack.gif)    
       ![] ]](rbrack.gif)     |
| 152 | 35, 42, 151 | ectocld 7814 |
. . . 4
    
        
   
            |
| 153 | 152 | impr 649 |
. . 3
    
                         |
| 154 | 34, 153 | sylan2b 492 |
. 2
    
                      |
| 155 | 13, 23, 33, 154 | fsumdvds 15030 |
1
                         |