Theorem sylow2a 18034

Description: A named lemma of Sylow's second and third theorems. If G is a finite P-group that acts on the finite set Y, then the set Z of all points of Y fixed by every element of G has cardinality equivalent to the cardinality of Y, mod P. (Contributed by Mario Carneiro, 17-Jan-2015.)

Hypotheses

Ref	Expression
sylow2a.x	|- X = ( Base ` G )
sylow2a.m	|- ( ph -> .(+) e. ( G GrpAct Y ) )
sylow2a.p	|- ( ph -> P pGrp G )
sylow2a.f	|- ( ph -> X e. Fin )
sylow2a.y	|- ( ph -> Y e. Fin )
sylow2a.z	|- Z = { u e. Y | A. h e. X ( h .(+) u ) = u }
sylow2a.r	|- .~ = { <. x , y >. | ( { x , y } C_ Y /\ E. g e. X ( g .(+) x ) = y ) }

Assertion

Ref	Expression
sylow2a	|- ( ph -> P || ( ( # ` Y ) - ( # ` Z ) ) )

Distinct variable groups:   .~ , h   g, h, u, x, y   g, G, x, y   .(+) , g, h, u, x, y   g, X, h, u, x, y   ph, h   g, Y, h, u, x, y

Allowed substitution hints:   ph( x, y, u, g)   P( x, y, u, g, h)   .~ ( x, y, u, g)   G( u, h)   Z( x, y, u, g, h)

Proof of Theorem sylow2a

Dummy variables w z are mutually distinct and distinct from all other variables.

Step	Hyp	Ref	Expression
1		sylow2a.x	. . 3 |- X = ( Base ` G )
2		sylow2a.m	. . 3 |- ( ph -> .(+) e. ( G GrpAct Y ) )
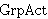3		sylow2a.p	. . 3 |- ( ph -> P pGrp G )
4		sylow2a.f	. . 3 |- ( ph -> X e. Fin )
5		sylow2a.y	. . 3 |- ( ph -> Y e. Fin )
6		sylow2a.z	. . 3 |- Z = { u e. Y | A. h e. X ( h .(+) u ) = u }
7		sylow2a.r	. . 3 |- .~ = { <. x , y >. | ( { x , y } C_ Y /\ E. g e. X ( g .(+) x ) = y ) }
8	1, 2, 3, 4, 5, 6, 7	sylow2alem2 18033	. 2 |- ( ph -> P || sum_ z e. ( ( Y /. .~ ) \ ~P Z ) ( # ` z ) )
9		inass 3823	. . . . . . 7 |- ( ( ( Y /. .~ ) i^i ~P Z ) i^i ( ( Y /. .~ ) \ ~P Z ) ) = ( ( Y /. .~ ) i^i ( ~P Z i^i ( ( Y /. .~ ) \ ~P Z ) ) )
10		disjdif 4040	. . . . . . . 8 |- ( ~P Z i^i ( ( Y /. .~ ) \ ~P Z ) ) = (/)
11	10	ineq2i 3811	. . . . . . 7 |- ( ( Y /. .~ ) i^i ( ~P Z i^i ( ( Y /. .~ ) \ ~P Z ) ) ) = ( ( Y /. .~ ) i^i (/) )
12		in0 3968	. . . . . . 7 |- ( ( Y /. .~ ) i^i (/) ) = (/)
13	9, 11, 12	3eqtri 2648	. . . . . 6 |- ( ( ( Y /. .~ ) i^i ~P Z ) i^i ( ( Y /. .~ ) \ ~P Z ) ) = (/)
14	13	a1i 11	. . . . 5 |- ( ph -> ( ( ( Y /. .~ ) i^i ~P Z ) i^i ( ( Y /. .~ ) \ ~P Z ) ) = (/) )
15		inundif 4046	. . . . . . 7 |- ( ( ( Y /. .~ ) i^i ~P Z ) u. ( ( Y /. .~ ) \ ~P Z ) ) = ( Y /. .~ )
16	15	eqcomi 2631	. . . . . 6 |- ( Y /. .~ ) = ( ( ( Y /. .~ ) i^i ~P Z ) u. ( ( Y /. .~ ) \ ~P Z ) )
17	16	a1i 11	. . . . 5 |- ( ph -> ( Y /. .~ ) = ( ( ( Y /. .~ ) i^i ~P Z ) u. ( ( Y /. .~ ) \ ~P Z ) ) )
18		pwfi 8261	. . . . . . 7 |- ( Y e. Fin <-> ~P Y e. Fin )
19	5, 18	sylib 208	. . . . . 6 |- ( ph -> ~P Y e. Fin )
20	7, 1	gaorber 17741	. . . . . . . 8 |- ( .(+) e. ( G GrpAct Y ) -> .~ Er Y )
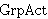
21	2, 20	syl 17	. . . . . . 7 |- ( ph -> .~ Er Y )
22	21	qsss 7808	. . . . . 6 |- ( ph -> ( Y /. .~ ) C_ ~P Y )
23	19, 22	ssfid 8183	. . . . 5 |- ( ph -> ( Y /. .~ ) e. Fin )
24	5	adantr 481	. . . . . . . 8 |- ( ( ph /\ z e. ( Y /. .~ ) ) -> Y e. Fin )
25	22	sselda 3603	. . . . . . . . 9 |- ( ( ph /\ z e. ( Y /. .~ ) ) -> z e. ~P Y )
26	25	elpwid 4170	. . . . . . . 8 |- ( ( ph /\ z e. ( Y /. .~ ) ) -> z C_ Y )
27	24, 26	ssfid 8183	. . . . . . 7 |- ( ( ph /\ z e. ( Y /. .~ ) ) -> z e. Fin )
28		hashcl 13147	. . . . . . 7 |- ( z e. Fin -> ( # ` z ) e. NN0 )
29	27, 28	syl 17	. . . . . 6 |- ( ( ph /\ z e. ( Y /. .~ ) ) -> ( # ` z ) e. NN0 )
30	29	nn0cnd 11353	. . . . 5 |- ( ( ph /\ z e. ( Y /. .~ ) ) -> ( # ` z ) e. CC )
31	14, 17, 23, 30	fsumsplit 14471	. . . 4 |- ( ph -> sum_ z e. ( Y /. .~ ) ( # ` z ) = ( sum_ z e. ( ( Y /. .~ ) i^i ~P Z ) ( # ` z ) + sum_ z e. ( ( Y /. .~ ) \ ~P Z ) ( # ` z ) ) )
32	21, 5	qshash 14559	. . . 4 |- ( ph -> ( # ` Y ) = sum_ z e. ( Y /. .~ ) ( # ` z ) )
33		inss1 3833	. . . . . . . 8 |- ( ( Y /. .~ ) i^i ~P Z ) C_ ( Y /. .~ )
34		ssfi 8180	. . . . . . . 8 |- ( ( ( Y /. .~ ) e. Fin /\ ( ( Y /. .~ ) i^i ~P Z ) C_ ( Y /. .~ ) ) -> ( ( Y /. .~ ) i^i ~P Z ) e. Fin )
35	23, 33, 34	sylancl 694	. . . . . . 7 |- ( ph -> ( ( Y /. .~ ) i^i ~P Z ) e. Fin )
36		ax-1cn 9994	. . . . . . 7 |- 1 e. CC
37		fsumconst 14522	. . . . . . 7 |- ( ( ( ( Y /. .~ ) i^i ~P Z ) e. Fin /\ 1 e. CC ) -> sum_ z e. ( ( Y /. .~ ) i^i ~P Z ) 1 = ( ( # ` ( ( Y /. .~ ) i^i ~P Z ) ) x. 1 ) )
38	35, 36, 37	sylancl 694	. . . . . 6 |- ( ph -> sum_ z e. ( ( Y /. .~ ) i^i ~P Z ) 1 = ( ( # ` ( ( Y /. .~ ) i^i ~P Z ) ) x. 1 ) )
39		elin 3796	. . . . . . . . . . 11 |- ( z e. ( ( Y /. .~ ) i^i ~P Z ) <-> ( z e. ( Y /. .~ ) /\ z e. ~P Z ) )
40		eqid 2622	. . . . . . . . . . . . 13 |- ( Y /. .~ ) = ( Y /. .~ )
41		sseq1 3626	. . . . . . . . . . . . . . 15 |- ( [ w ] .~ = z -> ( [ w ] .~ C_ Z <-> z C_ Z ) )
42		selpw 4165	. . . . . . . . . . . . . . 15 |- ( z e. ~P Z <-> z C_ Z )
43	41, 42	syl6bbr 278	. . . . . . . . . . . . . 14 |- ( [ w ] .~ = z -> ( [ w ] .~ C_ Z <-> z e. ~P Z ) )
44		breq1 4656	. . . . . . . . . . . . . 14 |- ( [ w ] .~ = z -> ( [ w ] .~ ~~ 1o <-> z ~~ 1o ) )
45	43, 44	imbi12d 334	. . . . . . . . . . . . 13 |- ( [ w ] .~ = z -> ( ( [ w ] .~ C_ Z -> [ w ] .~ ~~ 1o ) <-> ( z e. ~P Z -> z ~~ 1o ) ) )
46	21	adantr 481	. . . . . . . . . . . . . . . . 17 |- ( ( ph /\ w e. Y ) -> .~ Er Y )
47		simpr 477	. . . . . . . . . . . . . . . . 17 |- ( ( ph /\ w e. Y ) -> w e. Y )
48	46, 47	erref 7762	. . . . . . . . . . . . . . . 16 |- ( ( ph /\ w e. Y ) -> w .~ w )
49		vex 3203	. . . . . . . . . . . . . . . . 17 |- w e. _V
50	49, 49	elec 7786	. . . . . . . . . . . . . . . 16 |- ( w e. [ w ] .~ <-> w .~ w )
51	48, 50	sylibr 224	. . . . . . . . . . . . . . 15 |- ( ( ph /\ w e. Y ) -> w e. [ w ] .~ )
52		ssel 3597	. . . . . . . . . . . . . . 15 |- ( [ w ] .~ C_ Z -> ( w e. [ w ] .~ -> w e. Z ) )
53	51, 52	syl5com 31	. . . . . . . . . . . . . 14 |- ( ( ph /\ w e. Y ) -> ( [ w ] .~ C_ Z -> w e. Z ) )
54	1, 2, 3, 4, 5, 6, 7	sylow2alem1 18032	. . . . . . . . . . . . . . . . 17 |- ( ( ph /\ w e. Z ) -> [ w ] .~ = { w } )
55	49	ensn1 8020	. . . . . . . . . . . . . . . . 17 |- { w } ~~ 1o
56	54, 55	syl6eqbr 4692	. . . . . . . . . . . . . . . 16 |- ( ( ph /\ w e. Z ) -> [ w ] .~ ~~ 1o )
57	56	ex 450	. . . . . . . . . . . . . . 15 |- ( ph -> ( w e. Z -> [ w ] .~ ~~ 1o ) )
58	57	adantr 481	. . . . . . . . . . . . . 14 |- ( ( ph /\ w e. Y ) -> ( w e. Z -> [ w ] .~ ~~ 1o ) )
59	53, 58	syld 47	. . . . . . . . . . . . 13 |- ( ( ph /\ w e. Y ) -> ( [ w ] .~ C_ Z -> [ w ] .~ ~~ 1o ) )
60	40, 45, 59	ectocld 7814	. . . . . . . . . . . 12 |- ( ( ph /\ z e. ( Y /. .~ ) ) -> ( z e. ~P Z -> z ~~ 1o ) )
61	60	impr 649	. . . . . . . . . . 11 |- ( ( ph /\ ( z e. ( Y /. .~ ) /\ z e. ~P Z ) ) -> z ~~ 1o )
62	39, 61	sylan2b 492	. . . . . . . . . 10 |- ( ( ph /\ z e. ( ( Y /. .~ ) i^i ~P Z ) ) -> z ~~ 1o )
63		en1b 8024	. . . . . . . . . 10 |- ( z ~~ 1o <-> z = { U. z } )
64	62, 63	sylib 208	. . . . . . . . 9 |- ( ( ph /\ z e. ( ( Y /. .~ ) i^i ~P Z ) ) -> z = { U. z } )
65	64	fveq2d 6195	. . . . . . . 8 |- ( ( ph /\ z e. ( ( Y /. .~ ) i^i ~P Z ) ) -> ( # ` z ) = ( # ` { U. z } ) )
66		vuniex 6954	. . . . . . . . 9 |- U. z e. _V
67		hashsng 13159	. . . . . . . . 9 |- ( U. z e. _V -> ( # ` { U. z } ) = 1 )
68	66, 67	ax-mp 5	. . . . . . . 8 |- ( # ` { U. z } ) = 1
69	65, 68	syl6eq 2672	. . . . . . 7 |- ( ( ph /\ z e. ( ( Y /. .~ ) i^i ~P Z ) ) -> ( # ` z ) = 1 )
70	69	sumeq2dv 14433	. . . . . 6 |- ( ph -> sum_ z e. ( ( Y /. .~ ) i^i ~P Z ) ( # ` z ) = sum_ z e. ( ( Y /. .~ ) i^i ~P Z ) 1 )
71		ssrab2 3687	. . . . . . . . . . . 12 |- { u e. Y | A. h e. X ( h .(+) u ) = u } C_ Y
72	6, 71	eqsstri 3635	. . . . . . . . . . 11 |- Z C_ Y
73		ssfi 8180	. . . . . . . . . . 11 |- ( ( Y e. Fin /\ Z C_ Y ) -> Z e. Fin )
74	5, 72, 73	sylancl 694	. . . . . . . . . 10 |- ( ph -> Z e. Fin )
75		hashcl 13147	. . . . . . . . . 10 |- ( Z e. Fin -> ( # ` Z ) e. NN0 )
76	74, 75	syl 17	. . . . . . . . 9 |- ( ph -> ( # ` Z ) e. NN0 )
77	76	nn0cnd 11353	. . . . . . . 8 |- ( ph -> ( # ` Z ) e. CC )
78	77	mulid1d 10057	. . . . . . 7 |- ( ph -> ( ( # ` Z ) x. 1 ) = ( # ` Z ) )
79	6, 5	rabexd 4814	. . . . . . . . . 10 |- ( ph -> Z e. _V )
80		inss2 3834	. . . . . . . . . . 11 |- ( ( Y /. .~ ) i^i ~P Z ) C_ ~P Z
81		pwexg 4850	. . . . . . . . . . . 12 |- ( Z e. Fin -> ~P Z e. _V )
82	74, 81	syl 17	. . . . . . . . . . 11 |- ( ph -> ~P Z e. _V )
83		ssexg 4804	. . . . . . . . . . 11 |- ( ( ( ( Y /. .~ ) i^i ~P Z ) C_ ~P Z /\ ~P Z e. _V ) -> ( ( Y /. .~ ) i^i ~P Z ) e. _V )
84	80, 82, 83	sylancr 695	. . . . . . . . . 10 |- ( ph -> ( ( Y /. .~ ) i^i ~P Z ) e. _V )
85	7	relopabi 5245	. . . . . . . . . . . . . . . . 17 |- Rel .~
86		relssdmrn 5656	. . . . . . . . . . . . . . . . 17 |- ( Rel .~ -> .~ C_ ( dom .~ X. ran .~ ) )
87	85, 86	ax-mp 5	. . . . . . . . . . . . . . . 16 |- .~ C_ ( dom .~ X. ran .~ )
88		erdm 7752	. . . . . . . . . . . . . . . . . . 19 |- ( .~ Er Y -> dom .~ = Y )
89	21, 88	syl 17	. . . . . . . . . . . . . . . . . 18 |- ( ph -> dom .~ = Y )
90	89, 5	eqeltrd 2701	. . . . . . . . . . . . . . . . 17 |- ( ph -> dom .~ e. Fin )
91		errn 7764	. . . . . . . . . . . . . . . . . . 19 |- ( .~ Er Y -> ran .~ = Y )
92	21, 91	syl 17	. . . . . . . . . . . . . . . . . 18 |- ( ph -> ran .~ = Y )
93	92, 5	eqeltrd 2701	. . . . . . . . . . . . . . . . 17 |- ( ph -> ran .~ e. Fin )
94		xpexg 6960	. . . . . . . . . . . . . . . . 17 |- ( ( dom .~ e. Fin /\ ran .~ e. Fin ) -> ( dom .~ X. ran .~ ) e. _V )
95	90, 93, 94	syl2anc 693	. . . . . . . . . . . . . . . 16 |- ( ph -> ( dom .~ X. ran .~ ) e. _V )
96		ssexg 4804	. . . . . . . . . . . . . . . 16 |- ( ( .~ C_ ( dom .~ X. ran .~ ) /\ ( dom .~ X. ran .~ ) e. _V ) -> .~ e. _V )
97	87, 95, 96	sylancr 695	. . . . . . . . . . . . . . 15 |- ( ph -> .~ e. _V )
98	97	adantr 481	. . . . . . . . . . . . . 14 |- ( ( ph /\ w e. Z ) -> .~ e. _V )
99		simpr 477	. . . . . . . . . . . . . . 15 |- ( ( ph /\ w e. Z ) -> w e. Z )
100	72, 99	sseldi 3601	. . . . . . . . . . . . . 14 |- ( ( ph /\ w e. Z ) -> w e. Y )
101		ecelqsg 7802	. . . . . . . . . . . . . 14 |- ( ( .~ e. _V /\ w e. Y ) -> [ w ] .~ e. ( Y /. .~ ) )
102	98, 100, 101	syl2anc 693	. . . . . . . . . . . . 13 |- ( ( ph /\ w e. Z ) -> [ w ] .~ e. ( Y /. .~ ) )
103	54, 102	eqeltrrd 2702	. . . . . . . . . . . 12 |- ( ( ph /\ w e. Z ) -> { w } e. ( Y /. .~ ) )
104		snelpwi 4912	. . . . . . . . . . . . 13 |- ( w e. Z -> { w } e. ~P Z )
105	104	adantl 482	. . . . . . . . . . . 12 |- ( ( ph /\ w e. Z ) -> { w } e. ~P Z )
106	103, 105	elind 3798	. . . . . . . . . . 11 |- ( ( ph /\ w e. Z ) -> { w } e. ( ( Y /. .~ ) i^i ~P Z ) )
107	106	ex 450	. . . . . . . . . 10 |- ( ph -> ( w e. Z -> { w } e. ( ( Y /. .~ ) i^i ~P Z ) ) )
108		simpr 477	. . . . . . . . . . . . . . 15 |- ( ( ph /\ z e. ( ( Y /. .~ ) i^i ~P Z ) ) -> z e. ( ( Y /. .~ ) i^i ~P Z ) )
109	80, 108	sseldi 3601	. . . . . . . . . . . . . 14 |- ( ( ph /\ z e. ( ( Y /. .~ ) i^i ~P Z ) ) -> z e. ~P Z )
110	109	elpwid 4170	. . . . . . . . . . . . 13 |- ( ( ph /\ z e. ( ( Y /. .~ ) i^i ~P Z ) ) -> z C_ Z )
111	64, 110	eqsstr3d 3640	. . . . . . . . . . . 12 |- ( ( ph /\ z e. ( ( Y /. .~ ) i^i ~P Z ) ) -> { U. z } C_ Z )
112	66	snss 4316	. . . . . . . . . . . 12 |- ( U. z e. Z <-> { U. z } C_ Z )
113	111, 112	sylibr 224	. . . . . . . . . . 11 |- ( ( ph /\ z e. ( ( Y /. .~ ) i^i ~P Z ) ) -> U. z e. Z )
114	113	ex 450	. . . . . . . . . 10 |- ( ph -> ( z e. ( ( Y /. .~ ) i^i ~P Z ) -> U. z e. Z ) )
115		sneq 4187	. . . . . . . . . . . . . . 15 |- ( w = U. z -> { w } = { U. z } )
116	115	eqeq2d 2632	. . . . . . . . . . . . . 14 |- ( w = U. z -> ( z = { w } <-> z = { U. z } ) )
117	64, 116	syl5ibrcom 237	. . . . . . . . . . . . 13 |- ( ( ph /\ z e. ( ( Y /. .~ ) i^i ~P Z ) ) -> ( w = U. z -> z = { w } ) )
118	117	adantrl 752	. . . . . . . . . . . 12 |- ( ( ph /\ ( w e. Z /\ z e. ( ( Y /. .~ ) i^i ~P Z ) ) ) -> ( w = U. z -> z = { w } ) )
119		unieq 4444	. . . . . . . . . . . . 13 |- ( z = { w } -> U. z = U. { w } )
120	49	unisn 4451	. . . . . . . . . . . . 13 |- U. { w } = w
121	119, 120	syl6req 2673	. . . . . . . . . . . 12 |- ( z = { w } -> w = U. z )
122	118, 121	impbid1 215	. . . . . . . . . . 11 |- ( ( ph /\ ( w e. Z /\ z e. ( ( Y /. .~ ) i^i ~P Z ) ) ) -> ( w = U. z <-> z = { w } ) )
123	122	ex 450	. . . . . . . . . 10 |- ( ph -> ( ( w e. Z /\ z e. ( ( Y /. .~ ) i^i ~P Z ) ) -> ( w = U. z <-> z = { w } ) ) )
124	79, 84, 107, 114, 123	en3d 7992	. . . . . . . . 9 |- ( ph -> Z ~~ ( ( Y /. .~ ) i^i ~P Z ) )
125		hashen 13135	. . . . . . . . . 10 |- ( ( Z e. Fin /\ ( ( Y /. .~ ) i^i ~P Z ) e. Fin ) -> ( ( # ` Z ) = ( # ` ( ( Y /. .~ ) i^i ~P Z ) ) <-> Z ~~ ( ( Y /. .~ ) i^i ~P Z ) ) )
126	74, 35, 125	syl2anc 693	. . . . . . . . 9 |- ( ph -> ( ( # ` Z ) = ( # ` ( ( Y /. .~ ) i^i ~P Z ) ) <-> Z ~~ ( ( Y /. .~ ) i^i ~P Z ) ) )
127	124, 126	mpbird 247	. . . . . . . 8 |- ( ph -> ( # ` Z ) = ( # ` ( ( Y /. .~ ) i^i ~P Z ) ) )
128	127	oveq1d 6665	. . . . . . 7 |- ( ph -> ( ( # ` Z ) x. 1 ) = ( ( # ` ( ( Y /. .~ ) i^i ~P Z ) ) x. 1 ) )
129	78, 128	eqtr3d 2658	. . . . . 6 |- ( ph -> ( # ` Z ) = ( ( # ` ( ( Y /. .~ ) i^i ~P Z ) ) x. 1 ) )
130	38, 70, 129	3eqtr4rd 2667	. . . . 5 |- ( ph -> ( # ` Z ) = sum_ z e. ( ( Y /. .~ ) i^i ~P Z ) ( # ` z ) )
131	130	oveq1d 6665	. . . 4 |- ( ph -> ( ( # ` Z ) + sum_ z e. ( ( Y /. .~ ) \ ~P Z ) ( # ` z ) ) = ( sum_ z e. ( ( Y /. .~ ) i^i ~P Z ) ( # ` z ) + sum_ z e. ( ( Y /. .~ ) \ ~P Z ) ( # ` z ) ) )
132	31, 32, 131	3eqtr4rd 2667	. . 3 |- ( ph -> ( ( # ` Z ) + sum_ z e. ( ( Y /. .~ ) \ ~P Z ) ( # ` z ) ) = ( # ` Y ) )
133		hashcl 13147	. . . . . 6 |- ( Y e. Fin -> ( # ` Y ) e. NN0 )
134	5, 133	syl 17	. . . . 5 |- ( ph -> ( # ` Y ) e. NN0 )
135	134	nn0cnd 11353	. . . 4 |- ( ph -> ( # ` Y ) e. CC )
136		diffi 8192	. . . . . 6 |- ( ( Y /. .~ ) e. Fin -> ( ( Y /. .~ ) \ ~P Z ) e. Fin )
137	23, 136	syl 17	. . . . 5 |- ( ph -> ( ( Y /. .~ ) \ ~P Z ) e. Fin )
138		eldifi 3732	. . . . . 6 |- ( z e. ( ( Y /. .~ ) \ ~P Z ) -> z e. ( Y /. .~ ) )
139	138, 30	sylan2 491	. . . . 5 |- ( ( ph /\ z e. ( ( Y /. .~ ) \ ~P Z ) ) -> ( # ` z ) e. CC )
140	137, 139	fsumcl 14464	. . . 4 |- ( ph -> sum_ z e. ( ( Y /. .~ ) \ ~P Z ) ( # ` z ) e. CC )
141	135, 77, 140	subaddd 10410	. . 3 |- ( ph -> ( ( ( # ` Y ) - ( # ` Z ) ) = sum_ z e. ( ( Y /. .~ ) \ ~P Z ) ( # ` z ) <-> ( ( # ` Z ) + sum_ z e. ( ( Y /. .~ ) \ ~P Z ) ( # ` z ) ) = ( # ` Y ) ) )
142	132, 141	mpbird 247	. 2 |- ( ph -> ( ( # ` Y ) - ( # ` Z ) ) = sum_ z e. ( ( Y /. .~ ) \ ~P Z ) ( # ` z ) )
143	8, 142	breqtrrd 4681	1 |- ( ph -> P || ( ( # ` Y ) - ( # ` Z ) ) )

Syntax hints:   -> wi 4   <-> wb 196   /\ wa 384   = wceq 1483   e. wcel 1990   A.wral 2912   E.wrex 2913   {crab 2916   _Vcvv 3200   \ cdif 3571   u. cun 3572   i^i cin 3573   C_ wss 3574   (/)c0 3915   ~Pcpw 4158   {csn 4177   {cpr 4179   U.cuni 4436   class class class wbr 4653   {copab 4712   X. cxp 5112   dom cdm 5114   ran crn 5115   Rel wrel 5119   ` cfv 5888  (class class class)co 6650   1oc1o 7553   Er wer 7739   [cec 7740   /.cqs 7741   ~~ cen 7952   Fincfn 7955   CCcc 9934   1c1 9937   + caddc 9939   x. cmul 9941   - cmin 10266   NN0cn0 11292   #chash 13117   sum_csu 14416   || cdvds 14983   Basecbs 15857   GrpAct cga 17722   pGrp cpgp 17946

This theorem was proved from axioms:  ax-mp 5  ax-1 6  ax-2 7  ax-3 8  ax-gen 1722  ax-4 1737  ax-5 1839  ax-6 1888  ax-7 1935  ax-8 1992  ax-9 1999  ax-10 2019  ax-11 2034  ax-12 2047  ax-13 2246  ax-ext 2602  ax-rep 4771  ax-sep 4781  ax-nul 4789  ax-pow 4843  ax-pr 4906  ax-un 6949  ax-inf2 8538  ax-cnex 9992  ax-resscn 9993  ax-1cn 9994  ax-icn 9995  ax-addcl 9996  ax-addrcl 9997  ax-mulcl 9998  ax-mulrcl 9999  ax-mulcom 10000  ax-addass 10001  ax-mulass 10002  ax-distr 10003  ax-i2m1 10004  ax-1ne0 10005  ax-1rid 10006  ax-rnegex 10007  ax-rrecex 10008  ax-cnre 10009  ax-pre-lttri 10010  ax-pre-lttrn 10011  ax-pre-ltadd 10012  ax-pre-mulgt0 10013  ax-pre-sup 10014

This theorem depends on definitions:  df-bi 197  df-or 385  df-an 386  df-3or 1038  df-3an 1039  df-tru 1486  df-fal 1489  df-ex 1705  df-nf 1710  df-sb 1881  df-eu 2474  df-mo 2475  df-clab 2609  df-cleq 2615  df-clel 2618  df-nfc 2753  df-ne 2795  df-nel 2898  df-ral 2917  df-rex 2918  df-reu 2919  df-rmo 2920  df-rab 2921  df-v 3202  df-sbc 3436  df-csb 3534  df-dif 3577  df-un 3579  df-in 3581  df-ss 3588  df-pss 3590  df-nul 3916  df-if 4087  df-pw 4160  df-sn 4178  df-pr 4180  df-tp 4182  df-op 4184  df-uni 4437  df-int 4476  df-iun 4522  df-disj 4621  df-br 4654  df-opab 4713  df-mpt 4730  df-tr 4753  df-id 5024  df-eprel 5029  df-po 5035  df-so 5036  df-fr 5073  df-se 5074  df-we 5075  df-xp 5120  df-rel 5121  df-cnv 5122  df-co 5123  df-dm 5124  df-rn 5125  df-res 5126  df-ima 5127  df-pred 5680  df-ord 5726  df-on 5727  df-lim 5728  df-suc 5729  df-iota 5851  df-fun 5890  df-fn 5891  df-f 5892  df-f1 5893  df-fo 5894  df-f1o 5895  df-fv 5896  df-isom 5897  df-riota 6611  df-ov 6653  df-oprab 6654  df-mpt2 6655  df-om 7066  df-1st 7168  df-2nd 7169  df-wrecs 7407  df-recs 7468  df-rdg 7506  df-1o 7560  df-2o 7561  df-oadd 7564  df-omul 7565  df-er 7742  df-ec 7744  df-qs 7748  df-map 7859  df-en 7956  df-dom 7957  df-sdom 7958  df-fin 7959  df-sup 8348  df-inf 8349  df-oi 8415  df-card 8765  df-acn 8768  df-cda 8990  df-pnf 10076  df-mnf 10077  df-xr 10078  df-ltxr 10079  df-le 10080  df-sub 10268  df-neg 10269  df-div 10685  df-nn 11021  df-2 11079  df-3 11080  df-n0 11293  df-xnn0 11364  df-z 11378  df-uz 11688  df-q 11789  df-rp 11833  df-fz 12327  df-fzo 12466  df-fl 12593  df-mod 12669  df-seq 12802  df-exp 12861  df-fac 13061  df-bc 13090  df-hash 13118  df-cj 13839  df-re 13840  df-im 13841  df-sqrt 13975  df-abs 13976  df-clim 14219  df-sum 14417  df-dvds 14984  df-gcd 15217  df-prm 15386  df-pc 15542  df-ndx 15860  df-slot 15861  df-base 15863  df-sets 15864  df-ress 15865  df-plusg 15954  df-0g 16102  df-mgm 17242  df-sgrp 17284  df-mnd 17295  df-submnd 17336  df-grp 17425  df-minusg 17426  df-sbg 17427  df-mulg 17541  df-subg 17591  df-eqg 17593  df-ga 17723  df-od 17948  df-pgp 17950

This theorem is referenced by:  sylow2blem3  18037  sylow3lem6  18047