Theorem mdsymlem5 29266

Description: Lemma for mdsymi 29270. (Contributed by NM, 2-Jul-2004.) (New usage is discouraged.)

Hypotheses

Ref	Expression
mdsymlem1.1	|- A e. CH
mdsymlem1.2	|- B e. CH
mdsymlem1.3	|- C = ( A vH p )

Assertion

Ref	Expression
mdsymlem5	|- ( ( q e. HAtoms /\ r e. HAtoms ) -> ( -. q = p -> ( ( p C_ ( q vH r ) /\ ( q C_ A /\ r C_ B ) ) -> ( ( ( c e. CH /\ A C_ c ) /\ p e. HAtoms ) -> ( p C_ c -> p C_ ( ( c i^i B ) vH A ) ) ) ) ) )

Distinct variable groups:   r, q, C   p, c, q, r, A   B, c, p, q, r

Allowed substitution hints:   C( p, c)

Proof of Theorem mdsymlem5

Step	Hyp	Ref	Expression
1		df-ne 2795	. . . . . . . . . . . . . . . . . . . . . 22 |- ( q =/= p <-> -. q = p )
2		atnemeq0 29236	. . . . . . . . . . . . . . . . . . . . . 22 |- ( ( q e. HAtoms /\ p e. HAtoms ) -> ( q =/= p <-> ( q i^i p ) = 0H ) )
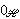3	1, 2	syl5bbr 274	. . . . . . . . . . . . . . . . . . . . 21 |- ( ( q e. HAtoms /\ p e. HAtoms ) -> ( -. q = p <-> ( q i^i p ) = 0H ) )
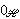4	3	anbi2d 740	. . . . . . . . . . . . . . . . . . . 20 |- ( ( q e. HAtoms /\ p e. HAtoms ) -> ( ( p C_ ( q vH r ) /\ -. q = p ) <-> ( p C_ ( q vH r ) /\ ( q i^i p ) = 0H ) ) )
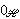5	4	3adant3 1081	. . . . . . . . . . . . . . . . . . 19 |- ( ( q e. HAtoms /\ p e. HAtoms /\ r e. HAtoms ) -> ( ( p C_ ( q vH r ) /\ -. q = p ) <-> ( p C_ ( q vH r ) /\ ( q i^i p ) = 0H ) ) )
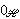6		atelch 29203	. . . . . . . . . . . . . . . . . . . 20 |- ( q e. HAtoms -> q e. CH )
7		atexch 29240	. . . . . . . . . . . . . . . . . . . 20 |- ( ( q e. CH /\ p e. HAtoms /\ r e. HAtoms ) -> ( ( p C_ ( q vH r ) /\ ( q i^i p ) = 0H ) -> r C_ ( q vH p ) ) )
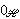8	6, 7	syl3an1 1359	. . . . . . . . . . . . . . . . . . 19 |- ( ( q e. HAtoms /\ p e. HAtoms /\ r e. HAtoms ) -> ( ( p C_ ( q vH r ) /\ ( q i^i p ) = 0H ) -> r C_ ( q vH p ) ) )
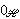
9	5, 8	sylbid 230	. . . . . . . . . . . . . . . . . 18 |- ( ( q e. HAtoms /\ p e. HAtoms /\ r e. HAtoms ) -> ( ( p C_ ( q vH r ) /\ -. q = p ) -> r C_ ( q vH p ) ) )
10	9	expd 452	. . . . . . . . . . . . . . . . 17 |- ( ( q e. HAtoms /\ p e. HAtoms /\ r e. HAtoms ) -> ( p C_ ( q vH r ) -> ( -. q = p -> r C_ ( q vH p ) ) ) )
11	10	3com23 1271	. . . . . . . . . . . . . . . 16 |- ( ( q e. HAtoms /\ r e. HAtoms /\ p e. HAtoms ) -> ( p C_ ( q vH r ) -> ( -. q = p -> r C_ ( q vH p ) ) ) )
12	11	3expa 1265	. . . . . . . . . . . . . . 15 |- ( ( ( q e. HAtoms /\ r e. HAtoms ) /\ p e. HAtoms ) -> ( p C_ ( q vH r ) -> ( -. q = p -> r C_ ( q vH p ) ) ) )
13	12	adantrl 752	. . . . . . . . . . . . . 14 |- ( ( ( q e. HAtoms /\ r e. HAtoms ) /\ ( c e. CH /\ p e. HAtoms ) ) -> ( p C_ ( q vH r ) -> ( -. q = p -> r C_ ( q vH p ) ) ) )
14	13	adantrd 484	. . . . . . . . . . . . 13 |- ( ( ( q e. HAtoms /\ r e. HAtoms ) /\ ( c e. CH /\ p e. HAtoms ) ) -> ( ( p C_ ( q vH r ) /\ ( q C_ A /\ r C_ B ) ) -> ( -. q = p -> r C_ ( q vH p ) ) ) )
15	14	imp32 449	. . . . . . . . . . . 12 |- ( ( ( ( q e. HAtoms /\ r e. HAtoms ) /\ ( c e. CH /\ p e. HAtoms ) ) /\ ( ( p C_ ( q vH r ) /\ ( q C_ A /\ r C_ B ) ) /\ -. q = p ) ) -> r C_ ( q vH p ) )
16	15	adantrl 752	. . . . . . . . . . 11 |- ( ( ( ( q e. HAtoms /\ r e. HAtoms ) /\ ( c e. CH /\ p e. HAtoms ) ) /\ ( A C_ c /\ ( ( p C_ ( q vH r ) /\ ( q C_ A /\ r C_ B ) ) /\ -. q = p ) ) ) -> r C_ ( q vH p ) )
17	16	adantrr 753	. . . . . . . . . 10 |- ( ( ( ( q e. HAtoms /\ r e. HAtoms ) /\ ( c e. CH /\ p e. HAtoms ) ) /\ ( ( A C_ c /\ ( ( p C_ ( q vH r ) /\ ( q C_ A /\ r C_ B ) ) /\ -. q = p ) ) /\ p C_ c ) ) -> r C_ ( q vH p ) )
18		simplrl 800	. . . . . . . . . . . 12 |- ( ( ( p C_ ( q vH r ) /\ ( q C_ A /\ r C_ B ) ) /\ -. q = p ) -> q C_ A )
19		atelch 29203	. . . . . . . . . . . . . . . 16 |- ( p e. HAtoms -> p e. CH )
20	19	anim1i 592	. . . . . . . . . . . . . . 15 |- ( ( p e. HAtoms /\ c e. CH ) -> ( p e. CH /\ c e. CH ) )
21	20	ancoms 469	. . . . . . . . . . . . . 14 |- ( ( c e. CH /\ p e. HAtoms ) -> ( p e. CH /\ c e. CH ) )
22		mdsymlem1.1	. . . . . . . . . . . . . . . . . . . . . . . . 25 |- A e. CH
23		chub2 28367	. . . . . . . . . . . . . . . . . . . . . . . . 25 |- ( ( A e. CH /\ c e. CH ) -> A C_ ( c vH A ) )
24	22, 23	mpan 706	. . . . . . . . . . . . . . . . . . . . . . . 24 |- ( c e. CH -> A C_ ( c vH A ) )
25		sstr 3611	. . . . . . . . . . . . . . . . . . . . . . . 24 |- ( ( q C_ A /\ A C_ ( c vH A ) ) -> q C_ ( c vH A ) )
26	24, 25	sylan2 491	. . . . . . . . . . . . . . . . . . . . . . 23 |- ( ( q C_ A /\ c e. CH ) -> q C_ ( c vH A ) )
27		chub1 28366	. . . . . . . . . . . . . . . . . . . . . . . . 25 |- ( ( c e. CH /\ A e. CH ) -> c C_ ( c vH A ) )
28	22, 27	mpan2 707	. . . . . . . . . . . . . . . . . . . . . . . 24 |- ( c e. CH -> c C_ ( c vH A ) )
29		sstr 3611	. . . . . . . . . . . . . . . . . . . . . . . 24 |- ( ( p C_ c /\ c C_ ( c vH A ) ) -> p C_ ( c vH A ) )
30	28, 29	sylan2 491	. . . . . . . . . . . . . . . . . . . . . . 23 |- ( ( p C_ c /\ c e. CH ) -> p C_ ( c vH A ) )
31	26, 30	anim12i 590	. . . . . . . . . . . . . . . . . . . . . 22 |- ( ( ( q C_ A /\ c e. CH ) /\ ( p C_ c /\ c e. CH ) ) -> ( q C_ ( c vH A ) /\ p C_ ( c vH A ) ) )
32	31	anandirs 874	. . . . . . . . . . . . . . . . . . . . 21 |- ( ( ( q C_ A /\ p C_ c ) /\ c e. CH ) -> ( q C_ ( c vH A ) /\ p C_ ( c vH A ) ) )
33	32	ancoms 469	. . . . . . . . . . . . . . . . . . . 20 |- ( ( c e. CH /\ ( q C_ A /\ p C_ c ) ) -> ( q C_ ( c vH A ) /\ p C_ ( c vH A ) ) )
34	33	adantll 750	. . . . . . . . . . . . . . . . . . 19 |- ( ( ( ( q e. CH /\ p e. CH ) /\ c e. CH ) /\ ( q C_ A /\ p C_ c ) ) -> ( q C_ ( c vH A ) /\ p C_ ( c vH A ) ) )
35		chjcl 28216	. . . . . . . . . . . . . . . . . . . . . . 23 |- ( ( c e. CH /\ A e. CH ) -> ( c vH A ) e. CH )
36	22, 35	mpan2 707	. . . . . . . . . . . . . . . . . . . . . 22 |- ( c e. CH -> ( c vH A ) e. CH )
37		chlub 28368	. . . . . . . . . . . . . . . . . . . . . 22 |- ( ( q e. CH /\ p e. CH /\ ( c vH A ) e. CH ) -> ( ( q C_ ( c vH A ) /\ p C_ ( c vH A ) ) <-> ( q vH p ) C_ ( c vH A ) ) )
38	36, 37	syl3an3 1361	. . . . . . . . . . . . . . . . . . . . 21 |- ( ( q e. CH /\ p e. CH /\ c e. CH ) -> ( ( q C_ ( c vH A ) /\ p C_ ( c vH A ) ) <-> ( q vH p ) C_ ( c vH A ) ) )
39	38	3expa 1265	. . . . . . . . . . . . . . . . . . . 20 |- ( ( ( q e. CH /\ p e. CH ) /\ c e. CH ) -> ( ( q C_ ( c vH A ) /\ p C_ ( c vH A ) ) <-> ( q vH p ) C_ ( c vH A ) ) )
40	39	adantr 481	. . . . . . . . . . . . . . . . . . 19 |- ( ( ( ( q e. CH /\ p e. CH ) /\ c e. CH ) /\ ( q C_ A /\ p C_ c ) ) -> ( ( q C_ ( c vH A ) /\ p C_ ( c vH A ) ) <-> ( q vH p ) C_ ( c vH A ) ) )
41	34, 40	mpbid 222	. . . . . . . . . . . . . . . . . 18 |- ( ( ( ( q e. CH /\ p e. CH ) /\ c e. CH ) /\ ( q C_ A /\ p C_ c ) ) -> ( q vH p ) C_ ( c vH A ) )
42	41	adantrl 752	. . . . . . . . . . . . . . . . 17 |- ( ( ( ( q e. CH /\ p e. CH ) /\ c e. CH ) /\ ( A C_ c /\ ( q C_ A /\ p C_ c ) ) ) -> ( q vH p ) C_ ( c vH A ) )
43		chlejb2 28372	. . . . . . . . . . . . . . . . . . . 20 |- ( ( A e. CH /\ c e. CH ) -> ( A C_ c <-> ( c vH A ) = c ) )
44	22, 43	mpan 706	. . . . . . . . . . . . . . . . . . 19 |- ( c e. CH -> ( A C_ c <-> ( c vH A ) = c ) )
45	44	biimpa 501	. . . . . . . . . . . . . . . . . 18 |- ( ( c e. CH /\ A C_ c ) -> ( c vH A ) = c )
46	45	ad2ant2lr 784	. . . . . . . . . . . . . . . . 17 |- ( ( ( ( q e. CH /\ p e. CH ) /\ c e. CH ) /\ ( A C_ c /\ ( q C_ A /\ p C_ c ) ) ) -> ( c vH A ) = c )
47	42, 46	sseqtrd 3641	. . . . . . . . . . . . . . . 16 |- ( ( ( ( q e. CH /\ p e. CH ) /\ c e. CH ) /\ ( A C_ c /\ ( q C_ A /\ p C_ c ) ) ) -> ( q vH p ) C_ c )
48	47	exp45 642	. . . . . . . . . . . . . . 15 |- ( ( ( q e. CH /\ p e. CH ) /\ c e. CH ) -> ( A C_ c -> ( q C_ A -> ( p C_ c -> ( q vH p ) C_ c ) ) ) )
49	48	anasss 679	. . . . . . . . . . . . . 14 |- ( ( q e. CH /\ ( p e. CH /\ c e. CH ) ) -> ( A C_ c -> ( q C_ A -> ( p C_ c -> ( q vH p ) C_ c ) ) ) )
50	6, 21, 49	syl2an 494	. . . . . . . . . . . . 13 |- ( ( q e. HAtoms /\ ( c e. CH /\ p e. HAtoms ) ) -> ( A C_ c -> ( q C_ A -> ( p C_ c -> ( q vH p ) C_ c ) ) ) )
51	50	adantlr 751	. . . . . . . . . . . 12 |- ( ( ( q e. HAtoms /\ r e. HAtoms ) /\ ( c e. CH /\ p e. HAtoms ) ) -> ( A C_ c -> ( q C_ A -> ( p C_ c -> ( q vH p ) C_ c ) ) ) )
52	18, 51	syl7 74	. . . . . . . . . . 11 |- ( ( ( q e. HAtoms /\ r e. HAtoms ) /\ ( c e. CH /\ p e. HAtoms ) ) -> ( A C_ c -> ( ( ( p C_ ( q vH r ) /\ ( q C_ A /\ r C_ B ) ) /\ -. q = p ) -> ( p C_ c -> ( q vH p ) C_ c ) ) ) )
53	52	imp44 622	. . . . . . . . . 10 |- ( ( ( ( q e. HAtoms /\ r e. HAtoms ) /\ ( c e. CH /\ p e. HAtoms ) ) /\ ( ( A C_ c /\ ( ( p C_ ( q vH r ) /\ ( q C_ A /\ r C_ B ) ) /\ -. q = p ) ) /\ p C_ c ) ) -> ( q vH p ) C_ c )
54	17, 53	sstrd 3613	. . . . . . . . 9 |- ( ( ( ( q e. HAtoms /\ r e. HAtoms ) /\ ( c e. CH /\ p e. HAtoms ) ) /\ ( ( A C_ c /\ ( ( p C_ ( q vH r ) /\ ( q C_ A /\ r C_ B ) ) /\ -. q = p ) ) /\ p C_ c ) ) -> r C_ c )
55		simplrr 801	. . . . . . . . . . 11 |- ( ( ( p C_ ( q vH r ) /\ ( q C_ A /\ r C_ B ) ) /\ -. q = p ) -> r C_ B )
56	55	ad2antlr 763	. . . . . . . . . 10 |- ( ( ( A C_ c /\ ( ( p C_ ( q vH r ) /\ ( q C_ A /\ r C_ B ) ) /\ -. q = p ) ) /\ p C_ c ) -> r C_ B )
57	56	adantl 482	. . . . . . . . 9 |- ( ( ( ( q e. HAtoms /\ r e. HAtoms ) /\ ( c e. CH /\ p e. HAtoms ) ) /\ ( ( A C_ c /\ ( ( p C_ ( q vH r ) /\ ( q C_ A /\ r C_ B ) ) /\ -. q = p ) ) /\ p C_ c ) ) -> r C_ B )
58	54, 57	ssind 3837	. . . . . . . 8 |- ( ( ( ( q e. HAtoms /\ r e. HAtoms ) /\ ( c e. CH /\ p e. HAtoms ) ) /\ ( ( A C_ c /\ ( ( p C_ ( q vH r ) /\ ( q C_ A /\ r C_ B ) ) /\ -. q = p ) ) /\ p C_ c ) ) -> r C_ ( c i^i B ) )
59		atelch 29203	. . . . . . . . . . . . . . . . 17 |- ( r e. HAtoms -> r e. CH )
60	6, 59	anim12i 590	. . . . . . . . . . . . . . . 16 |- ( ( q e. HAtoms /\ r e. HAtoms ) -> ( q e. CH /\ r e. CH ) )
61		mdsymlem1.2	. . . . . . . . . . . . . . . . . . . . . . . . 25 |- B e. CH
62		chincl 28358	. . . . . . . . . . . . . . . . . . . . . . . . 25 |- ( ( c e. CH /\ B e. CH ) -> ( c i^i B ) e. CH )
63	61, 62	mpan2 707	. . . . . . . . . . . . . . . . . . . . . . . 24 |- ( c e. CH -> ( c i^i B ) e. CH )
64		chlej1 28369	. . . . . . . . . . . . . . . . . . . . . . . . 25 |- ( ( ( r e. CH /\ ( c i^i B ) e. CH /\ q e. CH ) /\ r C_ ( c i^i B ) ) -> ( r vH q ) C_ ( ( c i^i B ) vH q ) )
65	64	ex 450	. . . . . . . . . . . . . . . . . . . . . . . 24 |- ( ( r e. CH /\ ( c i^i B ) e. CH /\ q e. CH ) -> ( r C_ ( c i^i B ) -> ( r vH q ) C_ ( ( c i^i B ) vH q ) ) )
66	63, 65	syl3an2 1360	. . . . . . . . . . . . . . . . . . . . . . 23 |- ( ( r e. CH /\ c e. CH /\ q e. CH ) -> ( r C_ ( c i^i B ) -> ( r vH q ) C_ ( ( c i^i B ) vH q ) ) )
67	66	3comr 1273	. . . . . . . . . . . . . . . . . . . . . 22 |- ( ( q e. CH /\ r e. CH /\ c e. CH ) -> ( r C_ ( c i^i B ) -> ( r vH q ) C_ ( ( c i^i B ) vH q ) ) )
68	67	3expa 1265	. . . . . . . . . . . . . . . . . . . . 21 |- ( ( ( q e. CH /\ r e. CH ) /\ c e. CH ) -> ( r C_ ( c i^i B ) -> ( r vH q ) C_ ( ( c i^i B ) vH q ) ) )
69	68	adantr 481	. . . . . . . . . . . . . . . . . . . 20 |- ( ( ( ( q e. CH /\ r e. CH ) /\ c e. CH ) /\ q C_ A ) -> ( r C_ ( c i^i B ) -> ( r vH q ) C_ ( ( c i^i B ) vH q ) ) )
70		chlej2 28370	. . . . . . . . . . . . . . . . . . . . . . . . 25 |- ( ( ( q e. CH /\ A e. CH /\ ( c i^i B ) e. CH ) /\ q C_ A ) -> ( ( c i^i B ) vH q ) C_ ( ( c i^i B ) vH A ) )
71	22, 70	mp3anl2 1419	. . . . . . . . . . . . . . . . . . . . . . . 24 |- ( ( ( q e. CH /\ ( c i^i B ) e. CH ) /\ q C_ A ) -> ( ( c i^i B ) vH q ) C_ ( ( c i^i B ) vH A ) )
72	63, 71	sylanl2 683	. . . . . . . . . . . . . . . . . . . . . . 23 |- ( ( ( q e. CH /\ c e. CH ) /\ q C_ A ) -> ( ( c i^i B ) vH q ) C_ ( ( c i^i B ) vH A ) )
73	72	adantllr 755	. . . . . . . . . . . . . . . . . . . . . 22 |- ( ( ( ( q e. CH /\ r e. CH ) /\ c e. CH ) /\ q C_ A ) -> ( ( c i^i B ) vH q ) C_ ( ( c i^i B ) vH A ) )
74		sstr2 3610	. . . . . . . . . . . . . . . . . . . . . 22 |- ( ( r vH q ) C_ ( ( c i^i B ) vH q ) -> ( ( ( c i^i B ) vH q ) C_ ( ( c i^i B ) vH A ) -> ( r vH q ) C_ ( ( c i^i B ) vH A ) ) )
75	73, 74	syl5com 31	. . . . . . . . . . . . . . . . . . . . 21 |- ( ( ( ( q e. CH /\ r e. CH ) /\ c e. CH ) /\ q C_ A ) -> ( ( r vH q ) C_ ( ( c i^i B ) vH q ) -> ( r vH q ) C_ ( ( c i^i B ) vH A ) ) )
76		chjcom 28365	. . . . . . . . . . . . . . . . . . . . . . 23 |- ( ( q e. CH /\ r e. CH ) -> ( q vH r ) = ( r vH q ) )
77	76	ad2antrr 762	. . . . . . . . . . . . . . . . . . . . . 22 |- ( ( ( ( q e. CH /\ r e. CH ) /\ c e. CH ) /\ q C_ A ) -> ( q vH r ) = ( r vH q ) )
78	77	sseq1d 3632	. . . . . . . . . . . . . . . . . . . . 21 |- ( ( ( ( q e. CH /\ r e. CH ) /\ c e. CH ) /\ q C_ A ) -> ( ( q vH r ) C_ ( ( c i^i B ) vH A ) <-> ( r vH q ) C_ ( ( c i^i B ) vH A ) ) )
79	75, 78	sylibrd 249	. . . . . . . . . . . . . . . . . . . 20 |- ( ( ( ( q e. CH /\ r e. CH ) /\ c e. CH ) /\ q C_ A ) -> ( ( r vH q ) C_ ( ( c i^i B ) vH q ) -> ( q vH r ) C_ ( ( c i^i B ) vH A ) ) )
80	69, 79	syld 47	. . . . . . . . . . . . . . . . . . 19 |- ( ( ( ( q e. CH /\ r e. CH ) /\ c e. CH ) /\ q C_ A ) -> ( r C_ ( c i^i B ) -> ( q vH r ) C_ ( ( c i^i B ) vH A ) ) )
81	80	adantrl 752	. . . . . . . . . . . . . . . . . 18 |- ( ( ( ( q e. CH /\ r e. CH ) /\ c e. CH ) /\ ( p C_ ( q vH r ) /\ q C_ A ) ) -> ( r C_ ( c i^i B ) -> ( q vH r ) C_ ( ( c i^i B ) vH A ) ) )
82		sstr2 3610	. . . . . . . . . . . . . . . . . . 19 |- ( p C_ ( q vH r ) -> ( ( q vH r ) C_ ( ( c i^i B ) vH A ) -> p C_ ( ( c i^i B ) vH A ) ) )
83	82	ad2antrl 764	. . . . . . . . . . . . . . . . . 18 |- ( ( ( ( q e. CH /\ r e. CH ) /\ c e. CH ) /\ ( p C_ ( q vH r ) /\ q C_ A ) ) -> ( ( q vH r ) C_ ( ( c i^i B ) vH A ) -> p C_ ( ( c i^i B ) vH A ) ) )
84	81, 83	syld 47	. . . . . . . . . . . . . . . . 17 |- ( ( ( ( q e. CH /\ r e. CH ) /\ c e. CH ) /\ ( p C_ ( q vH r ) /\ q C_ A ) ) -> ( r C_ ( c i^i B ) -> p C_ ( ( c i^i B ) vH A ) ) )
85	84	exp32 631	. . . . . . . . . . . . . . . 16 |- ( ( ( q e. CH /\ r e. CH ) /\ c e. CH ) -> ( p C_ ( q vH r ) -> ( q C_ A -> ( r C_ ( c i^i B ) -> p C_ ( ( c i^i B ) vH A ) ) ) ) )
86	60, 85	sylan 488	. . . . . . . . . . . . . . 15 |- ( ( ( q e. HAtoms /\ r e. HAtoms ) /\ c e. CH ) -> ( p C_ ( q vH r ) -> ( q C_ A -> ( r C_ ( c i^i B ) -> p C_ ( ( c i^i B ) vH A ) ) ) ) )
87	86	adantrr 753	. . . . . . . . . . . . . 14 |- ( ( ( q e. HAtoms /\ r e. HAtoms ) /\ ( c e. CH /\ p e. HAtoms ) ) -> ( p C_ ( q vH r ) -> ( q C_ A -> ( r C_ ( c i^i B ) -> p C_ ( ( c i^i B ) vH A ) ) ) ) )
88	87	imp31 448	. . . . . . . . . . . . 13 |- ( ( ( ( ( q e. HAtoms /\ r e. HAtoms ) /\ ( c e. CH /\ p e. HAtoms ) ) /\ p C_ ( q vH r ) ) /\ q C_ A ) -> ( r C_ ( c i^i B ) -> p C_ ( ( c i^i B ) vH A ) ) )
89	88	adantrr 753	. . . . . . . . . . . 12 |- ( ( ( ( ( q e. HAtoms /\ r e. HAtoms ) /\ ( c e. CH /\ p e. HAtoms ) ) /\ p C_ ( q vH r ) ) /\ ( q C_ A /\ r C_ B ) ) -> ( r C_ ( c i^i B ) -> p C_ ( ( c i^i B ) vH A ) ) )
90	89	anasss 679	. . . . . . . . . . 11 |- ( ( ( ( q e. HAtoms /\ r e. HAtoms ) /\ ( c e. CH /\ p e. HAtoms ) ) /\ ( p C_ ( q vH r ) /\ ( q C_ A /\ r C_ B ) ) ) -> ( r C_ ( c i^i B ) -> p C_ ( ( c i^i B ) vH A ) ) )
91	90	adantrr 753	. . . . . . . . . 10 |- ( ( ( ( q e. HAtoms /\ r e. HAtoms ) /\ ( c e. CH /\ p e. HAtoms ) ) /\ ( ( p C_ ( q vH r ) /\ ( q C_ A /\ r C_ B ) ) /\ -. q = p ) ) -> ( r C_ ( c i^i B ) -> p C_ ( ( c i^i B ) vH A ) ) )
92	91	adantrl 752	. . . . . . . . 9 |- ( ( ( ( q e. HAtoms /\ r e. HAtoms ) /\ ( c e. CH /\ p e. HAtoms ) ) /\ ( A C_ c /\ ( ( p C_ ( q vH r ) /\ ( q C_ A /\ r C_ B ) ) /\ -. q = p ) ) ) -> ( r C_ ( c i^i B ) -> p C_ ( ( c i^i B ) vH A ) ) )
93	92	adantrr 753	. . . . . . . 8 |- ( ( ( ( q e. HAtoms /\ r e. HAtoms ) /\ ( c e. CH /\ p e. HAtoms ) ) /\ ( ( A C_ c /\ ( ( p C_ ( q vH r ) /\ ( q C_ A /\ r C_ B ) ) /\ -. q = p ) ) /\ p C_ c ) ) -> ( r C_ ( c i^i B ) -> p C_ ( ( c i^i B ) vH A ) ) )
94	58, 93	mpd 15	. . . . . . 7 |- ( ( ( ( q e. HAtoms /\ r e. HAtoms ) /\ ( c e. CH /\ p e. HAtoms ) ) /\ ( ( A C_ c /\ ( ( p C_ ( q vH r ) /\ ( q C_ A /\ r C_ B ) ) /\ -. q = p ) ) /\ p C_ c ) ) -> p C_ ( ( c i^i B ) vH A ) )
95	94	exp32 631	. . . . . 6 |- ( ( ( q e. HAtoms /\ r e. HAtoms ) /\ ( c e. CH /\ p e. HAtoms ) ) -> ( ( A C_ c /\ ( ( p C_ ( q vH r ) /\ ( q C_ A /\ r C_ B ) ) /\ -. q = p ) ) -> ( p C_ c -> p C_ ( ( c i^i B ) vH A ) ) ) )
96	95	exp4d 637	. . . . 5 |- ( ( ( q e. HAtoms /\ r e. HAtoms ) /\ ( c e. CH /\ p e. HAtoms ) ) -> ( A C_ c -> ( ( p C_ ( q vH r ) /\ ( q C_ A /\ r C_ B ) ) -> ( -. q = p -> ( p C_ c -> p C_ ( ( c i^i B ) vH A ) ) ) ) ) )
97	96	exp32 631	. . . 4 |- ( ( q e. HAtoms /\ r e. HAtoms ) -> ( c e. CH -> ( p e. HAtoms -> ( A C_ c -> ( ( p C_ ( q vH r ) /\ ( q C_ A /\ r C_ B ) ) -> ( -. q = p -> ( p C_ c -> p C_ ( ( c i^i B ) vH A ) ) ) ) ) ) ) )
98	97	com34 91	. . 3 |- ( ( q e. HAtoms /\ r e. HAtoms ) -> ( c e. CH -> ( A C_ c -> ( p e. HAtoms -> ( ( p C_ ( q vH r ) /\ ( q C_ A /\ r C_ B ) ) -> ( -. q = p -> ( p C_ c -> p C_ ( ( c i^i B ) vH A ) ) ) ) ) ) ) )
99	98	imp4c 617	. 2 |- ( ( q e. HAtoms /\ r e. HAtoms ) -> ( ( ( c e. CH /\ A C_ c ) /\ p e. HAtoms ) -> ( ( p C_ ( q vH r ) /\ ( q C_ A /\ r C_ B ) ) -> ( -. q = p -> ( p C_ c -> p C_ ( ( c i^i B ) vH A ) ) ) ) ) )
100	99	com24 95	1 |- ( ( q e. HAtoms /\ r e. HAtoms ) -> ( -. q = p -> ( ( p C_ ( q vH r ) /\ ( q C_ A /\ r C_ B ) ) -> ( ( ( c e. CH /\ A C_ c ) /\ p e. HAtoms ) -> ( p C_ c -> p C_ ( ( c i^i B ) vH A ) ) ) ) ) )

Syntax hints:   -. wn 3   -> wi 4   <-> wb 196   /\ wa 384   /\ w3a 1037   = wceq 1483   e. wcel 1990   =/= wne 2794   i^i cin 3573   C_ wss 3574  (class class class)co 6650   CHcch 27786   vH chj 27790   0Hc0h 27792  HAtomscat 27822

This theorem was proved from axioms:  ax-mp 5  ax-1 6  ax-2 7  ax-3 8  ax-gen 1722  ax-4 1737  ax-5 1839  ax-6 1888  ax-7 1935  ax-8 1992  ax-9 1999  ax-10 2019  ax-11 2034  ax-12 2047  ax-13 2246  ax-ext 2602  ax-rep 4771  ax-sep 4781  ax-nul 4789  ax-pow 4843  ax-pr 4906  ax-un 6949  ax-inf2 8538  ax-cc 9257  ax-cnex 9992  ax-resscn 9993  ax-1cn 9994  ax-icn 9995  ax-addcl 9996  ax-addrcl 9997  ax-mulcl 9998  ax-mulrcl 9999  ax-mulcom 10000  ax-addass 10001  ax-mulass 10002  ax-distr 10003  ax-i2m1 10004  ax-1ne0 10005  ax-1rid 10006  ax-rnegex 10007  ax-rrecex 10008  ax-cnre 10009  ax-pre-lttri 10010  ax-pre-lttrn 10011  ax-pre-ltadd 10012  ax-pre-mulgt0 10013  ax-pre-sup 10014  ax-addf 10015  ax-mulf 10016  ax-hilex 27856  ax-hfvadd 27857  ax-hvcom 27858  ax-hvass 27859  ax-hv0cl 27860  ax-hvaddid 27861  ax-hfvmul 27862  ax-hvmulid 27863  ax-hvmulass 27864  ax-hvdistr1 27865  ax-hvdistr2 27866  ax-hvmul0 27867  ax-hfi 27936  ax-his1 27939  ax-his2 27940  ax-his3 27941  ax-his4 27942  ax-hcompl 28059

This theorem depends on definitions:  df-bi 197  df-or 385  df-an 386  df-3or 1038  df-3an 1039  df-tru 1486  df-fal 1489  df-ex 1705  df-nf 1710  df-sb 1881  df-eu 2474  df-mo 2475  df-clab 2609  df-cleq 2615  df-clel 2618  df-nfc 2753  df-ne 2795  df-nel 2898  df-ral 2917  df-rex 2918  df-reu 2919  df-rmo 2920  df-rab 2921  df-v 3202  df-sbc 3436  df-csb 3534  df-dif 3577  df-un 3579  df-in 3581  df-ss 3588  df-pss 3590  df-nul 3916  df-if 4087  df-pw 4160  df-sn 4178  df-pr 4180  df-tp 4182  df-op 4184  df-uni 4437  df-int 4476  df-iun 4522  df-iin 4523  df-br 4654  df-opab 4713  df-mpt 4730  df-tr 4753  df-id 5024  df-eprel 5029  df-po 5035  df-so 5036  df-fr 5073  df-se 5074  df-we 5075  df-xp 5120  df-rel 5121  df-cnv 5122  df-co 5123  df-dm 5124  df-rn 5125  df-res 5126  df-ima 5127  df-pred 5680  df-ord 5726  df-on 5727  df-lim 5728  df-suc 5729  df-iota 5851  df-fun 5890  df-fn 5891  df-f 5892  df-f1 5893  df-fo 5894  df-f1o 5895  df-fv 5896  df-isom 5897  df-riota 6611  df-ov 6653  df-oprab 6654  df-mpt2 6655  df-of 6897  df-om 7066  df-1st 7168  df-2nd 7169  df-supp 7296  df-wrecs 7407  df-recs 7468  df-rdg 7506  df-1o 7560  df-2o 7561  df-oadd 7564  df-omul 7565  df-er 7742  df-map 7859  df-pm 7860  df-ixp 7909  df-en 7956  df-dom 7957  df-sdom 7958  df-fin 7959  df-fsupp 8276  df-fi 8317  df-sup 8348  df-inf 8349  df-oi 8415  df-card 8765  df-acn 8768  df-cda 8990  df-pnf 10076  df-mnf 10077  df-xr 10078  df-ltxr 10079  df-le 10080  df-sub 10268  df-neg 10269  df-div 10685  df-nn 11021  df-2 11079  df-3 11080  df-4 11081  df-5 11082  df-6 11083  df-7 11084  df-8 11085  df-9 11086  df-n0 11293  df-z 11378  df-dec 11494  df-uz 11688  df-q 11789  df-rp 11833  df-xneg 11946  df-xadd 11947  df-xmul 11948  df-ioo 12179  df-ico 12181  df-icc 12182  df-fz 12327  df-fzo 12466  df-fl 12593  df-seq 12802  df-exp 12861  df-hash 13118  df-cj 13839  df-re 13840  df-im 13841  df-sqrt 13975  df-abs 13976  df-clim 14219  df-rlim 14220  df-sum 14417  df-struct 15859  df-ndx 15860  df-slot 15861  df-base 15863  df-sets 15864  df-ress 15865  df-plusg 15954  df-mulr 15955  df-starv 15956  df-sca 15957  df-vsca 15958  df-ip 15959  df-tset 15960  df-ple 15961  df-ds 15964  df-unif 15965  df-hom 15966  df-cco 15967  df-rest 16083  df-topn 16084  df-0g 16102  df-gsum 16103  df-topgen 16104  df-pt 16105  df-prds 16108  df-xrs 16162  df-qtop 16167  df-imas 16168  df-xps 16170  df-mre 16246  df-mrc 16247  df-acs 16249  df-mgm 17242  df-sgrp 17284  df-mnd 17295  df-submnd 17336  df-mulg 17541  df-cntz 17750  df-cmn 18195  df-psmet 19738  df-xmet 19739  df-met 19740  df-bl 19741  df-mopn 19742  df-fbas 19743  df-fg 19744  df-cnfld 19747  df-top 20699  df-topon 20716  df-topsp 20737  df-bases 20750  df-cld 20823  df-ntr 20824  df-cls 20825  df-nei 20902  df-cn 21031  df-cnp 21032  df-lm 21033  df-haus 21119  df-tx 21365  df-hmeo 21558  df-fil 21650  df-fm 21742  df-flim 21743  df-flf 21744  df-xms 22125  df-ms 22126  df-tms 22127  df-cfil 23053  df-cau 23054  df-cmet 23055  df-grpo 27347  df-gid 27348  df-ginv 27349  df-gdiv 27350  df-ablo 27399  df-vc 27414  df-nv 27447  df-va 27450  df-ba 27451  df-sm 27452  df-0v 27453  df-vs 27454  df-nmcv 27455  df-ims 27456  df-dip 27556  df-ssp 27577  df-ph 27668  df-cbn 27719  df-hnorm 27825  df-hba 27826  df-hvsub 27828  df-hlim 27829  df-hcau 27830  df-sh 28064  df-ch 28078  df-oc 28109  df-ch0 28110  df-shs 28167  df-span 28168  df-chj 28169  df-chsup 28170  df-pjh 28254  df-cv 29138  df-at 29197

This theorem is referenced by:  mdsymlem6  29267