Theorem opsqrlem6 29004

Description: Lemma for opsqri . (Contributed by NM, 23-Aug-2006.) (New usage is discouraged.)

Hypotheses

Ref	Expression
opsqrlem2.1	|- T e. HrmOp
opsqrlem2.2	|- S = ( x e. HrmOp , y e. HrmOp |-> ( x +op ( ( 1 / 2 ) .op ( T -op ( x o. x ) ) ) ) )
opsqrlem2.3	|- F = seq 1 ( S , ( NN X. { 0hop } ) )
opsqrlem6.4	|- T <_op Iop

Assertion

Ref	Expression
opsqrlem6	|- ( N e. NN -> ( F ` N ) <_op Iop )

Distinct variable group:   x, y, T

Allowed substitution hints:   S( x, y)   F( x, y)   N( x, y)

Proof of Theorem opsqrlem6

Dummy variables j k are mutually distinct and distinct from all other variables.

Step	Hyp	Ref	Expression
1		fveq2 6191	. . 3 |- ( j = 1 -> ( F ` j ) = ( F ` 1 ) )
2	1	breq1d 4663	. 2 |- ( j = 1 -> ( ( F ` j ) <_op Iop <-> ( F ` 1 ) <_op Iop ) )
3		fveq2 6191	. . 3 |- ( j = ( k + 1 ) -> ( F ` j ) = ( F ` ( k + 1 ) ) )
4	3	breq1d 4663	. 2 |- ( j = ( k + 1 ) -> ( ( F ` j ) <_op Iop <-> ( F ` ( k + 1 ) ) <_op Iop ) )
5		fveq2 6191	. . 3 |- ( j = N -> ( F ` j ) = ( F ` N ) )
6	5	breq1d 4663	. 2 |- ( j = N -> ( ( F ` j ) <_op Iop <-> ( F ` N ) <_op Iop ) )
7		opsqrlem2.1	. . . 4 |- T e. HrmOp
8		opsqrlem2.2	. . . 4 |- S = ( x e. HrmOp , y e. HrmOp |-> ( x +op ( ( 1 / 2 ) .op ( T -op ( x o. x ) ) ) ) )
9		opsqrlem2.3	. . . 4 |- F = seq 1 ( S , ( NN X. { 0hop } ) )
10	7, 8, 9	opsqrlem2 29000	. . 3 |- ( F ` 1 ) = 0hop
11		idleop 28990	. . 3 |- 0hop <_op Iop
12	10, 11	eqbrtri 4674	. 2 |- ( F ` 1 ) <_op Iop
13		idhmop 28841	. . . . . . . 8 |- Iop e. HrmOp
14	7, 8, 9	opsqrlem4 29002	. . . . . . . . 9 |- F : NN --> HrmOp
15	14	ffvelrni 6358	. . . . . . . 8 |- ( k e. NN -> ( F ` k ) e. HrmOp )
16		hmopd 28881	. . . . . . . 8 |- ( ( Iop e. HrmOp /\ ( F ` k ) e. HrmOp ) -> ( Iop -op ( F ` k ) ) e. HrmOp )
17	13, 15, 16	sylancr 695	. . . . . . 7 |- ( k e. NN -> ( Iop -op ( F ` k ) ) e. HrmOp )
18		eqid 2622	. . . . . . . 8 |- ( ( Iop -op ( F ` k ) ) o. ( Iop -op ( F ` k ) ) ) = ( ( Iop -op ( F ` k ) ) o. ( Iop -op ( F ` k ) ) )
19		hmopco 28882	. . . . . . . 8 |- ( ( ( Iop -op ( F ` k ) ) e. HrmOp /\ ( Iop -op ( F ` k ) ) e. HrmOp /\ ( ( Iop -op ( F ` k ) ) o. ( Iop -op ( F ` k ) ) ) = ( ( Iop -op ( F ` k ) ) o. ( Iop -op ( F ` k ) ) ) ) -> ( ( Iop -op ( F ` k ) ) o. ( Iop -op ( F ` k ) ) ) e. HrmOp )
20	18, 19	mp3an3 1413	. . . . . . 7 |- ( ( ( Iop -op ( F ` k ) ) e. HrmOp /\ ( Iop -op ( F ` k ) ) e. HrmOp ) -> ( ( Iop -op ( F ` k ) ) o. ( Iop -op ( F ` k ) ) ) e. HrmOp )
21	17, 17, 20	syl2anc 693	. . . . . 6 |- ( k e. NN -> ( ( Iop -op ( F ` k ) ) o. ( Iop -op ( F ` k ) ) ) e. HrmOp )
22		leopsq 28988	. . . . . . 7 |- ( ( Iop -op ( F ` k ) ) e. HrmOp -> 0hop <_op ( ( Iop -op ( F ` k ) ) o. ( Iop -op ( F ` k ) ) ) )
23	17, 22	syl 17	. . . . . 6 |- ( k e. NN -> 0hop <_op ( ( Iop -op ( F ` k ) ) o. ( Iop -op ( F ` k ) ) ) )
24		opsqrlem6.4	. . . . . . . 8 |- T <_op Iop
25		leop3 28984	. . . . . . . . 9 |- ( ( T e. HrmOp /\ Iop e. HrmOp ) -> ( T <_op Iop <-> 0hop <_op ( Iop -op T ) ) )
26	7, 13, 25	mp2an 708	. . . . . . . 8 |- ( T <_op Iop <-> 0hop <_op ( Iop -op T ) )
27	24, 26	mpbi 220	. . . . . . 7 |- 0hop <_op ( Iop -op T )
28		hmopd 28881	. . . . . . . . 9 |- ( ( Iop e. HrmOp /\ T e. HrmOp ) -> ( Iop -op T ) e. HrmOp )
29	13, 7, 28	mp2an 708	. . . . . . . 8 |- ( Iop -op T ) e. HrmOp
30		leopadd 28991	. . . . . . . 8 |- ( ( ( ( ( Iop -op ( F ` k ) ) o. ( Iop -op ( F ` k ) ) ) e. HrmOp /\ ( Iop -op T ) e. HrmOp ) /\ ( 0hop <_op ( ( Iop -op ( F ` k ) ) o. ( Iop -op ( F ` k ) ) ) /\ 0hop <_op ( Iop -op T ) ) ) -> 0hop <_op ( ( ( Iop -op ( F ` k ) ) o. ( Iop -op ( F ` k ) ) ) +op ( Iop -op T ) ) )
31	29, 30	mpanl2 717	. . . . . . 7 |- ( ( ( ( Iop -op ( F ` k ) ) o. ( Iop -op ( F ` k ) ) ) e. HrmOp /\ ( 0hop <_op ( ( Iop -op ( F ` k ) ) o. ( Iop -op ( F ` k ) ) ) /\ 0hop <_op ( Iop -op T ) ) ) -> 0hop <_op ( ( ( Iop -op ( F ` k ) ) o. ( Iop -op ( F ` k ) ) ) +op ( Iop -op T ) ) )
32	27, 31	mpanr2 720	. . . . . 6 |- ( ( ( ( Iop -op ( F ` k ) ) o. ( Iop -op ( F ` k ) ) ) e. HrmOp /\ 0hop <_op ( ( Iop -op ( F ` k ) ) o. ( Iop -op ( F ` k ) ) ) ) -> 0hop <_op ( ( ( Iop -op ( F ` k ) ) o. ( Iop -op ( F ` k ) ) ) +op ( Iop -op T ) ) )
33	21, 23, 32	syl2anc 693	. . . . 5 |- ( k e. NN -> 0hop <_op ( ( ( Iop -op ( F ` k ) ) o. ( Iop -op ( F ` k ) ) ) +op ( Iop -op T ) ) )
34		2cn 11091	. . . . . . . . . 10 |- 2 e. CC
35		hmopf 28733	. . . . . . . . . . 11 |- ( ( F ` k ) e. HrmOp -> ( F ` k ) : ~H --> ~H )
36	15, 35	syl 17	. . . . . . . . . 10 |- ( k e. NN -> ( F ` k ) : ~H --> ~H )
37		homulcl 28618	. . . . . . . . . 10 |- ( ( 2 e. CC /\ ( F ` k ) : ~H --> ~H ) -> ( 2 .op ( F ` k ) ) : ~H --> ~H )
38	34, 36, 37	sylancr 695	. . . . . . . . 9 |- ( k e. NN -> ( 2 .op ( F ` k ) ) : ~H --> ~H )
39		hmopf 28733	. . . . . . . . . . 11 |- ( T e. HrmOp -> T : ~H --> ~H )
40	7, 39	ax-mp 5	. . . . . . . . . 10 |- T : ~H --> ~H
41		fco 6058	. . . . . . . . . . 11 |- ( ( ( F ` k ) : ~H --> ~H /\ ( F ` k ) : ~H --> ~H ) -> ( ( F ` k ) o. ( F ` k ) ) : ~H --> ~H )
42	36, 36, 41	syl2anc 693	. . . . . . . . . 10 |- ( k e. NN -> ( ( F ` k ) o. ( F ` k ) ) : ~H --> ~H )
43		hosubcl 28632	. . . . . . . . . 10 |- ( ( T : ~H --> ~H /\ ( ( F ` k ) o. ( F ` k ) ) : ~H --> ~H ) -> ( T -op ( ( F ` k ) o. ( F ` k ) ) ) : ~H --> ~H )
44	40, 42, 43	sylancr 695	. . . . . . . . 9 |- ( k e. NN -> ( T -op ( ( F ` k ) o. ( F ` k ) ) ) : ~H --> ~H )
45		hmopf 28733	. . . . . . . . . . . 12 |- ( Iop e. HrmOp -> Iop : ~H --> ~H )
46	13, 45	ax-mp 5	. . . . . . . . . . 11 |- Iop : ~H --> ~H
47		homulcl 28618	. . . . . . . . . . 11 |- ( ( 2 e. CC /\ Iop : ~H --> ~H ) -> ( 2 .op Iop ) : ~H --> ~H )
48	34, 46, 47	mp2an 708	. . . . . . . . . 10 |- ( 2 .op Iop ) : ~H --> ~H
49		hosubsub4 28677	. . . . . . . . . 10 |- ( ( ( 2 .op Iop ) : ~H --> ~H /\ ( 2 .op ( F ` k ) ) : ~H --> ~H /\ ( T -op ( ( F ` k ) o. ( F ` k ) ) ) : ~H --> ~H ) -> ( ( ( 2 .op Iop ) -op ( 2 .op ( F ` k ) ) ) -op ( T -op ( ( F ` k ) o. ( F ` k ) ) ) ) = ( ( 2 .op Iop ) -op ( ( 2 .op ( F ` k ) ) +op ( T -op ( ( F ` k ) o. ( F ` k ) ) ) ) ) )
50	48, 49	mp3an1 1411	. . . . . . . . 9 |- ( ( ( 2 .op ( F ` k ) ) : ~H --> ~H /\ ( T -op ( ( F ` k ) o. ( F ` k ) ) ) : ~H --> ~H ) -> ( ( ( 2 .op Iop ) -op ( 2 .op ( F ` k ) ) ) -op ( T -op ( ( F ` k ) o. ( F ` k ) ) ) ) = ( ( 2 .op Iop ) -op ( ( 2 .op ( F ` k ) ) +op ( T -op ( ( F ` k ) o. ( F ` k ) ) ) ) ) )
51	38, 44, 50	syl2anc 693	. . . . . . . 8 |- ( k e. NN -> ( ( ( 2 .op Iop ) -op ( 2 .op ( F ` k ) ) ) -op ( T -op ( ( F ` k ) o. ( F ` k ) ) ) ) = ( ( 2 .op Iop ) -op ( ( 2 .op ( F ` k ) ) +op ( T -op ( ( F ` k ) o. ( F ` k ) ) ) ) ) )
52		hosubcl 28632	. . . . . . . . . . . . . . 15 |- ( ( ( ( F ` k ) o. ( F ` k ) ) : ~H --> ~H /\ ( 2 .op ( F ` k ) ) : ~H --> ~H ) -> ( ( ( F ` k ) o. ( F ` k ) ) -op ( 2 .op ( F ` k ) ) ) : ~H --> ~H )
53	42, 38, 52	syl2anc 693	. . . . . . . . . . . . . 14 |- ( k e. NN -> ( ( ( F ` k ) o. ( F ` k ) ) -op ( 2 .op ( F ` k ) ) ) : ~H --> ~H )
54		hoadd32 28642	. . . . . . . . . . . . . . 15 |- ( ( Iop : ~H --> ~H /\ ( ( ( F ` k ) o. ( F ` k ) ) -op ( 2 .op ( F ` k ) ) ) : ~H --> ~H /\ Iop : ~H --> ~H ) -> ( ( Iop +op ( ( ( F ` k ) o. ( F ` k ) ) -op ( 2 .op ( F ` k ) ) ) ) +op Iop ) = ( ( Iop +op Iop ) +op ( ( ( F ` k ) o. ( F ` k ) ) -op ( 2 .op ( F ` k ) ) ) ) )
55	46, 46, 54	mp3an13 1415	. . . . . . . . . . . . . 14 |- ( ( ( ( F ` k ) o. ( F ` k ) ) -op ( 2 .op ( F ` k ) ) ) : ~H --> ~H -> ( ( Iop +op ( ( ( F ` k ) o. ( F ` k ) ) -op ( 2 .op ( F ` k ) ) ) ) +op Iop ) = ( ( Iop +op Iop ) +op ( ( ( F ` k ) o. ( F ` k ) ) -op ( 2 .op ( F ` k ) ) ) ) )
56	53, 55	syl 17	. . . . . . . . . . . . 13 |- ( k e. NN -> ( ( Iop +op ( ( ( F ` k ) o. ( F ` k ) ) -op ( 2 .op ( F ` k ) ) ) ) +op Iop ) = ( ( Iop +op Iop ) +op ( ( ( F ` k ) o. ( F ` k ) ) -op ( 2 .op ( F ` k ) ) ) ) )
57		ho2times 28678	. . . . . . . . . . . . . . 15 |- ( Iop : ~H --> ~H -> ( 2 .op Iop ) = ( Iop +op Iop ) )
58	46, 57	ax-mp 5	. . . . . . . . . . . . . 14 |- ( 2 .op Iop ) = ( Iop +op Iop )
59	58	oveq1i 6660	. . . . . . . . . . . . 13 |- ( ( 2 .op Iop ) +op ( ( ( F ` k ) o. ( F ` k ) ) -op ( 2 .op ( F ` k ) ) ) ) = ( ( Iop +op Iop ) +op ( ( ( F ` k ) o. ( F ` k ) ) -op ( 2 .op ( F ` k ) ) ) )
60	56, 59	syl6eqr 2674	. . . . . . . . . . . 12 |- ( k e. NN -> ( ( Iop +op ( ( ( F ` k ) o. ( F ` k ) ) -op ( 2 .op ( F ` k ) ) ) ) +op Iop ) = ( ( 2 .op Iop ) +op ( ( ( F ` k ) o. ( F ` k ) ) -op ( 2 .op ( F ` k ) ) ) ) )
61		hoaddsubass 28674	. . . . . . . . . . . . . 14 |- ( ( ( 2 .op Iop ) : ~H --> ~H /\ ( ( F ` k ) o. ( F ` k ) ) : ~H --> ~H /\ ( 2 .op ( F ` k ) ) : ~H --> ~H ) -> ( ( ( 2 .op Iop ) +op ( ( F ` k ) o. ( F ` k ) ) ) -op ( 2 .op ( F ` k ) ) ) = ( ( 2 .op Iop ) +op ( ( ( F ` k ) o. ( F ` k ) ) -op ( 2 .op ( F ` k ) ) ) ) )
62	48, 61	mp3an1 1411	. . . . . . . . . . . . 13 |- ( ( ( ( F ` k ) o. ( F ` k ) ) : ~H --> ~H /\ ( 2 .op ( F ` k ) ) : ~H --> ~H ) -> ( ( ( 2 .op Iop ) +op ( ( F ` k ) o. ( F ` k ) ) ) -op ( 2 .op ( F ` k ) ) ) = ( ( 2 .op Iop ) +op ( ( ( F ` k ) o. ( F ` k ) ) -op ( 2 .op ( F ` k ) ) ) ) )
63	42, 38, 62	syl2anc 693	. . . . . . . . . . . 12 |- ( k e. NN -> ( ( ( 2 .op Iop ) +op ( ( F ` k ) o. ( F ` k ) ) ) -op ( 2 .op ( F ` k ) ) ) = ( ( 2 .op Iop ) +op ( ( ( F ` k ) o. ( F ` k ) ) -op ( 2 .op ( F ` k ) ) ) ) )
64	60, 63	eqtr4d 2659	. . . . . . . . . . 11 |- ( k e. NN -> ( ( Iop +op ( ( ( F ` k ) o. ( F ` k ) ) -op ( 2 .op ( F ` k ) ) ) ) +op Iop ) = ( ( ( 2 .op Iop ) +op ( ( F ` k ) o. ( F ` k ) ) ) -op ( 2 .op ( F ` k ) ) ) )
65	64	oveq1d 6665	. . . . . . . . . 10 |- ( k e. NN -> ( ( ( Iop +op ( ( ( F ` k ) o. ( F ` k ) ) -op ( 2 .op ( F ` k ) ) ) ) +op Iop ) -op T ) = ( ( ( ( 2 .op Iop ) +op ( ( F ` k ) o. ( F ` k ) ) ) -op ( 2 .op ( F ` k ) ) ) -op T ) )
66		hoaddcl 28617	. . . . . . . . . . . 12 |- ( ( Iop : ~H --> ~H /\ ( ( ( F ` k ) o. ( F ` k ) ) -op ( 2 .op ( F ` k ) ) ) : ~H --> ~H ) -> ( Iop +op ( ( ( F ` k ) o. ( F ` k ) ) -op ( 2 .op ( F ` k ) ) ) ) : ~H --> ~H )
67	46, 53, 66	sylancr 695	. . . . . . . . . . 11 |- ( k e. NN -> ( Iop +op ( ( ( F ` k ) o. ( F ` k ) ) -op ( 2 .op ( F ` k ) ) ) ) : ~H --> ~H )
68		hoaddsubass 28674	. . . . . . . . . . . 12 |- ( ( ( Iop +op ( ( ( F ` k ) o. ( F ` k ) ) -op ( 2 .op ( F ` k ) ) ) ) : ~H --> ~H /\ Iop : ~H --> ~H /\ T : ~H --> ~H ) -> ( ( ( Iop +op ( ( ( F ` k ) o. ( F ` k ) ) -op ( 2 .op ( F ` k ) ) ) ) +op Iop ) -op T ) = ( ( Iop +op ( ( ( F ` k ) o. ( F ` k ) ) -op ( 2 .op ( F ` k ) ) ) ) +op ( Iop -op T ) ) )
69	46, 40, 68	mp3an23 1416	. . . . . . . . . . 11 |- ( ( Iop +op ( ( ( F ` k ) o. ( F ` k ) ) -op ( 2 .op ( F ` k ) ) ) ) : ~H --> ~H -> ( ( ( Iop +op ( ( ( F ` k ) o. ( F ` k ) ) -op ( 2 .op ( F ` k ) ) ) ) +op Iop ) -op T ) = ( ( Iop +op ( ( ( F ` k ) o. ( F ` k ) ) -op ( 2 .op ( F ` k ) ) ) ) +op ( Iop -op T ) ) )
70	67, 69	syl 17	. . . . . . . . . 10 |- ( k e. NN -> ( ( ( Iop +op ( ( ( F ` k ) o. ( F ` k ) ) -op ( 2 .op ( F ` k ) ) ) ) +op Iop ) -op T ) = ( ( Iop +op ( ( ( F ` k ) o. ( F ` k ) ) -op ( 2 .op ( F ` k ) ) ) ) +op ( Iop -op T ) ) )
71		hoaddcl 28617	. . . . . . . . . . . 12 |- ( ( ( 2 .op Iop ) : ~H --> ~H /\ ( ( F ` k ) o. ( F ` k ) ) : ~H --> ~H ) -> ( ( 2 .op Iop ) +op ( ( F ` k ) o. ( F ` k ) ) ) : ~H --> ~H )
72	48, 42, 71	sylancr 695	. . . . . . . . . . 11 |- ( k e. NN -> ( ( 2 .op Iop ) +op ( ( F ` k ) o. ( F ` k ) ) ) : ~H --> ~H )
73		hosubsub4 28677	. . . . . . . . . . . 12 |- ( ( ( ( 2 .op Iop ) +op ( ( F ` k ) o. ( F ` k ) ) ) : ~H --> ~H /\ ( 2 .op ( F ` k ) ) : ~H --> ~H /\ T : ~H --> ~H ) -> ( ( ( ( 2 .op Iop ) +op ( ( F ` k ) o. ( F ` k ) ) ) -op ( 2 .op ( F ` k ) ) ) -op T ) = ( ( ( 2 .op Iop ) +op ( ( F ` k ) o. ( F ` k ) ) ) -op ( ( 2 .op ( F ` k ) ) +op T ) ) )
74	40, 73	mp3an3 1413	. . . . . . . . . . 11 |- ( ( ( ( 2 .op Iop ) +op ( ( F ` k ) o. ( F ` k ) ) ) : ~H --> ~H /\ ( 2 .op ( F ` k ) ) : ~H --> ~H ) -> ( ( ( ( 2 .op Iop ) +op ( ( F ` k ) o. ( F ` k ) ) ) -op ( 2 .op ( F ` k ) ) ) -op T ) = ( ( ( 2 .op Iop ) +op ( ( F ` k ) o. ( F ` k ) ) ) -op ( ( 2 .op ( F ` k ) ) +op T ) ) )
75	72, 38, 74	syl2anc 693	. . . . . . . . . 10 |- ( k e. NN -> ( ( ( ( 2 .op Iop ) +op ( ( F ` k ) o. ( F ` k ) ) ) -op ( 2 .op ( F ` k ) ) ) -op T ) = ( ( ( 2 .op Iop ) +op ( ( F ` k ) o. ( F ` k ) ) ) -op ( ( 2 .op ( F ` k ) ) +op T ) ) )
76	65, 70, 75	3eqtr3d 2664	. . . . . . . . 9 |- ( k e. NN -> ( ( Iop +op ( ( ( F ` k ) o. ( F ` k ) ) -op ( 2 .op ( F ` k ) ) ) ) +op ( Iop -op T ) ) = ( ( ( 2 .op Iop ) +op ( ( F ` k ) o. ( F ` k ) ) ) -op ( ( 2 .op ( F ` k ) ) +op T ) ) )
77		hosubadd4 28673	. . . . . . . . . . . 12 |- ( ( ( ( 2 .op Iop ) : ~H --> ~H /\ ( 2 .op ( F ` k ) ) : ~H --> ~H ) /\ ( T : ~H --> ~H /\ ( ( F ` k ) o. ( F ` k ) ) : ~H --> ~H ) ) -> ( ( ( 2 .op Iop ) -op ( 2 .op ( F ` k ) ) ) -op ( T -op ( ( F ` k ) o. ( F ` k ) ) ) ) = ( ( ( 2 .op Iop ) +op ( ( F ` k ) o. ( F ` k ) ) ) -op ( ( 2 .op ( F ` k ) ) +op T ) ) )
78	40, 77	mpanr1 719	. . . . . . . . . . 11 |- ( ( ( ( 2 .op Iop ) : ~H --> ~H /\ ( 2 .op ( F ` k ) ) : ~H --> ~H ) /\ ( ( F ` k ) o. ( F ` k ) ) : ~H --> ~H ) -> ( ( ( 2 .op Iop ) -op ( 2 .op ( F ` k ) ) ) -op ( T -op ( ( F ` k ) o. ( F ` k ) ) ) ) = ( ( ( 2 .op Iop ) +op ( ( F ` k ) o. ( F ` k ) ) ) -op ( ( 2 .op ( F ` k ) ) +op T ) ) )
79	48, 78	mpanl1 716	. . . . . . . . . 10 |- ( ( ( 2 .op ( F ` k ) ) : ~H --> ~H /\ ( ( F ` k ) o. ( F ` k ) ) : ~H --> ~H ) -> ( ( ( 2 .op Iop ) -op ( 2 .op ( F ` k ) ) ) -op ( T -op ( ( F ` k ) o. ( F ` k ) ) ) ) = ( ( ( 2 .op Iop ) +op ( ( F ` k ) o. ( F ` k ) ) ) -op ( ( 2 .op ( F ` k ) ) +op T ) ) )
80	38, 42, 79	syl2anc 693	. . . . . . . . 9 |- ( k e. NN -> ( ( ( 2 .op Iop ) -op ( 2 .op ( F ` k ) ) ) -op ( T -op ( ( F ` k ) o. ( F ` k ) ) ) ) = ( ( ( 2 .op Iop ) +op ( ( F ` k ) o. ( F ` k ) ) ) -op ( ( 2 .op ( F ` k ) ) +op T ) ) )
81	76, 80	eqtr4d 2659	. . . . . . . 8 |- ( k e. NN -> ( ( Iop +op ( ( ( F ` k ) o. ( F ` k ) ) -op ( 2 .op ( F ` k ) ) ) ) +op ( Iop -op T ) ) = ( ( ( 2 .op Iop ) -op ( 2 .op ( F ` k ) ) ) -op ( T -op ( ( F ` k ) o. ( F ` k ) ) ) ) )
82		halfcn 11247	. . . . . . . . . . . 12 |- ( 1 / 2 ) e. CC
83		homulcl 28618	. . . . . . . . . . . 12 |- ( ( ( 1 / 2 ) e. CC /\ ( T -op ( ( F ` k ) o. ( F ` k ) ) ) : ~H --> ~H ) -> ( ( 1 / 2 ) .op ( T -op ( ( F ` k ) o. ( F ` k ) ) ) ) : ~H --> ~H )
84	82, 44, 83	sylancr 695	. . . . . . . . . . 11 |- ( k e. NN -> ( ( 1 / 2 ) .op ( T -op ( ( F ` k ) o. ( F ` k ) ) ) ) : ~H --> ~H )
85		hoadddi 28662	. . . . . . . . . . . 12 |- ( ( 2 e. CC /\ ( F ` k ) : ~H --> ~H /\ ( ( 1 / 2 ) .op ( T -op ( ( F ` k ) o. ( F ` k ) ) ) ) : ~H --> ~H ) -> ( 2 .op ( ( F ` k ) +op ( ( 1 / 2 ) .op ( T -op ( ( F ` k ) o. ( F ` k ) ) ) ) ) ) = ( ( 2 .op ( F ` k ) ) +op ( 2 .op ( ( 1 / 2 ) .op ( T -op ( ( F ` k ) o. ( F ` k ) ) ) ) ) ) )
86	34, 85	mp3an1 1411	. . . . . . . . . . 11 |- ( ( ( F ` k ) : ~H --> ~H /\ ( ( 1 / 2 ) .op ( T -op ( ( F ` k ) o. ( F ` k ) ) ) ) : ~H --> ~H ) -> ( 2 .op ( ( F ` k ) +op ( ( 1 / 2 ) .op ( T -op ( ( F ` k ) o. ( F ` k ) ) ) ) ) ) = ( ( 2 .op ( F ` k ) ) +op ( 2 .op ( ( 1 / 2 ) .op ( T -op ( ( F ` k ) o. ( F ` k ) ) ) ) ) ) )
87	36, 84, 86	syl2anc 693	. . . . . . . . . 10 |- ( k e. NN -> ( 2 .op ( ( F ` k ) +op ( ( 1 / 2 ) .op ( T -op ( ( F ` k ) o. ( F ` k ) ) ) ) ) ) = ( ( 2 .op ( F ` k ) ) +op ( 2 .op ( ( 1 / 2 ) .op ( T -op ( ( F ` k ) o. ( F ` k ) ) ) ) ) ) )
88		2ne0 11113	. . . . . . . . . . . . . 14 |- 2 =/= 0
89	34, 88	recidi 10756	. . . . . . . . . . . . 13 |- ( 2 x. ( 1 / 2 ) ) = 1
90	89	oveq1i 6660	. . . . . . . . . . . 12 |- ( ( 2 x. ( 1 / 2 ) ) .op ( T -op ( ( F ` k ) o. ( F ` k ) ) ) ) = ( 1 .op ( T -op ( ( F ` k ) o. ( F ` k ) ) ) )
91		homulass 28661	. . . . . . . . . . . . . 14 |- ( ( 2 e. CC /\ ( 1 / 2 ) e. CC /\ ( T -op ( ( F ` k ) o. ( F ` k ) ) ) : ~H --> ~H ) -> ( ( 2 x. ( 1 / 2 ) ) .op ( T -op ( ( F ` k ) o. ( F ` k ) ) ) ) = ( 2 .op ( ( 1 / 2 ) .op ( T -op ( ( F ` k ) o. ( F ` k ) ) ) ) ) )
92	34, 82, 91	mp3an12 1414	. . . . . . . . . . . . 13 |- ( ( T -op ( ( F ` k ) o. ( F ` k ) ) ) : ~H --> ~H -> ( ( 2 x. ( 1 / 2 ) ) .op ( T -op ( ( F ` k ) o. ( F ` k ) ) ) ) = ( 2 .op ( ( 1 / 2 ) .op ( T -op ( ( F ` k ) o. ( F ` k ) ) ) ) ) )
93	44, 92	syl 17	. . . . . . . . . . . 12 |- ( k e. NN -> ( ( 2 x. ( 1 / 2 ) ) .op ( T -op ( ( F ` k ) o. ( F ` k ) ) ) ) = ( 2 .op ( ( 1 / 2 ) .op ( T -op ( ( F ` k ) o. ( F ` k ) ) ) ) ) )
94		homulid2 28659	. . . . . . . . . . . . 13 |- ( ( T -op ( ( F ` k ) o. ( F ` k ) ) ) : ~H --> ~H -> ( 1 .op ( T -op ( ( F ` k ) o. ( F ` k ) ) ) ) = ( T -op ( ( F ` k ) o. ( F ` k ) ) ) )
95	44, 94	syl 17	. . . . . . . . . . . 12 |- ( k e. NN -> ( 1 .op ( T -op ( ( F ` k ) o. ( F ` k ) ) ) ) = ( T -op ( ( F ` k ) o. ( F ` k ) ) ) )
96	90, 93, 95	3eqtr3a 2680	. . . . . . . . . . 11 |- ( k e. NN -> ( 2 .op ( ( 1 / 2 ) .op ( T -op ( ( F ` k ) o. ( F ` k ) ) ) ) ) = ( T -op ( ( F ` k ) o. ( F ` k ) ) ) )
97	96	oveq2d 6666	. . . . . . . . . 10 |- ( k e. NN -> ( ( 2 .op ( F ` k ) ) +op ( 2 .op ( ( 1 / 2 ) .op ( T -op ( ( F ` k ) o. ( F ` k ) ) ) ) ) ) = ( ( 2 .op ( F ` k ) ) +op ( T -op ( ( F ` k ) o. ( F ` k ) ) ) ) )
98	87, 97	eqtrd 2656	. . . . . . . . 9 |- ( k e. NN -> ( 2 .op ( ( F ` k ) +op ( ( 1 / 2 ) .op ( T -op ( ( F ` k ) o. ( F ` k ) ) ) ) ) ) = ( ( 2 .op ( F ` k ) ) +op ( T -op ( ( F ` k ) o. ( F ` k ) ) ) ) )
99	98	oveq2d 6666	. . . . . . . 8 |- ( k e. NN -> ( ( 2 .op Iop ) -op ( 2 .op ( ( F ` k ) +op ( ( 1 / 2 ) .op ( T -op ( ( F ` k ) o. ( F ` k ) ) ) ) ) ) ) = ( ( 2 .op Iop ) -op ( ( 2 .op ( F ` k ) ) +op ( T -op ( ( F ` k ) o. ( F ` k ) ) ) ) ) )
100	51, 81, 99	3eqtr4d 2666	. . . . . . 7 |- ( k e. NN -> ( ( Iop +op ( ( ( F ` k ) o. ( F ` k ) ) -op ( 2 .op ( F ` k ) ) ) ) +op ( Iop -op T ) ) = ( ( 2 .op Iop ) -op ( 2 .op ( ( F ` k ) +op ( ( 1 / 2 ) .op ( T -op ( ( F ` k ) o. ( F ` k ) ) ) ) ) ) ) )
101		hoaddcl 28617	. . . . . . . . 9 |- ( ( ( F ` k ) : ~H --> ~H /\ ( ( 1 / 2 ) .op ( T -op ( ( F ` k ) o. ( F ` k ) ) ) ) : ~H --> ~H ) -> ( ( F ` k ) +op ( ( 1 / 2 ) .op ( T -op ( ( F ` k ) o. ( F ` k ) ) ) ) ) : ~H --> ~H )
102	36, 84, 101	syl2anc 693	. . . . . . . 8 |- ( k e. NN -> ( ( F ` k ) +op ( ( 1 / 2 ) .op ( T -op ( ( F ` k ) o. ( F ` k ) ) ) ) ) : ~H --> ~H )
103		hosubdi 28667	. . . . . . . . 9 |- ( ( 2 e. CC /\ Iop : ~H --> ~H /\ ( ( F ` k ) +op ( ( 1 / 2 ) .op ( T -op ( ( F ` k ) o. ( F ` k ) ) ) ) ) : ~H --> ~H ) -> ( 2 .op ( Iop -op ( ( F ` k ) +op ( ( 1 / 2 ) .op ( T -op ( ( F ` k ) o. ( F ` k ) ) ) ) ) ) ) = ( ( 2 .op Iop ) -op ( 2 .op ( ( F ` k ) +op ( ( 1 / 2 ) .op ( T -op ( ( F ` k ) o. ( F ` k ) ) ) ) ) ) ) )
104	34, 46, 103	mp3an12 1414	. . . . . . . 8 |- ( ( ( F ` k ) +op ( ( 1 / 2 ) .op ( T -op ( ( F ` k ) o. ( F ` k ) ) ) ) ) : ~H --> ~H -> ( 2 .op ( Iop -op ( ( F ` k ) +op ( ( 1 / 2 ) .op ( T -op ( ( F ` k ) o. ( F ` k ) ) ) ) ) ) ) = ( ( 2 .op Iop ) -op ( 2 .op ( ( F ` k ) +op ( ( 1 / 2 ) .op ( T -op ( ( F ` k ) o. ( F ` k ) ) ) ) ) ) ) )
105	102, 104	syl 17	. . . . . . 7 |- ( k e. NN -> ( 2 .op ( Iop -op ( ( F ` k ) +op ( ( 1 / 2 ) .op ( T -op ( ( F ` k ) o. ( F ` k ) ) ) ) ) ) ) = ( ( 2 .op Iop ) -op ( 2 .op ( ( F ` k ) +op ( ( 1 / 2 ) .op ( T -op ( ( F ` k ) o. ( F ` k ) ) ) ) ) ) ) )
106	100, 105	eqtr4d 2659	. . . . . 6 |- ( k e. NN -> ( ( Iop +op ( ( ( F ` k ) o. ( F ` k ) ) -op ( 2 .op ( F ` k ) ) ) ) +op ( Iop -op T ) ) = ( 2 .op ( Iop -op ( ( F ` k ) +op ( ( 1 / 2 ) .op ( T -op ( ( F ` k ) o. ( F ` k ) ) ) ) ) ) ) )
107		hosubcl 28632	. . . . . . . . . 10 |- ( ( Iop : ~H --> ~H /\ ( F ` k ) : ~H --> ~H ) -> ( Iop -op ( F ` k ) ) : ~H --> ~H )
108	46, 36, 107	sylancr 695	. . . . . . . . 9 |- ( k e. NN -> ( Iop -op ( F ` k ) ) : ~H --> ~H )
109		hocsubdir 28644	. . . . . . . . . 10 |- ( ( Iop : ~H --> ~H /\ ( F ` k ) : ~H --> ~H /\ ( Iop -op ( F ` k ) ) : ~H --> ~H ) -> ( ( Iop -op ( F ` k ) ) o. ( Iop -op ( F ` k ) ) ) = ( ( Iop o. ( Iop -op ( F ` k ) ) ) -op ( ( F ` k ) o. ( Iop -op ( F ` k ) ) ) ) )
110	46, 109	mp3an1 1411	. . . . . . . . 9 |- ( ( ( F ` k ) : ~H --> ~H /\ ( Iop -op ( F ` k ) ) : ~H --> ~H ) -> ( ( Iop -op ( F ` k ) ) o. ( Iop -op ( F ` k ) ) ) = ( ( Iop o. ( Iop -op ( F ` k ) ) ) -op ( ( F ` k ) o. ( Iop -op ( F ` k ) ) ) ) )
111	36, 108, 110	syl2anc 693	. . . . . . . 8 |- ( k e. NN -> ( ( Iop -op ( F ` k ) ) o. ( Iop -op ( F ` k ) ) ) = ( ( Iop o. ( Iop -op ( F ` k ) ) ) -op ( ( F ` k ) o. ( Iop -op ( F ` k ) ) ) ) )
112		hmoplin 28801	. . . . . . . . . . . . . . 15 |- ( Iop e. HrmOp -> Iop e. LinOp )
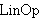113	13, 112	ax-mp 5	. . . . . . . . . . . . . 14 |- Iop e. LinOp
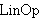114		hoddi 28849	. . . . . . . . . . . . . 14 |- ( ( Iop e. LinOp /\ Iop : ~H --> ~H /\ ( F ` k ) : ~H --> ~H ) -> ( Iop o. ( Iop -op ( F ` k ) ) ) = ( ( Iop o. Iop ) -op ( Iop o. ( F ` k ) ) ) )
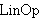
115	113, 46, 114	mp3an12 1414	. . . . . . . . . . . . 13 |- ( ( F ` k ) : ~H --> ~H -> ( Iop o. ( Iop -op ( F ` k ) ) ) = ( ( Iop o. Iop ) -op ( Iop o. ( F ` k ) ) ) )
116	36, 115	syl 17	. . . . . . . . . . . 12 |- ( k e. NN -> ( Iop o. ( Iop -op ( F ` k ) ) ) = ( ( Iop o. Iop ) -op ( Iop o. ( F ` k ) ) ) )
117	46	hoid1i 28648	. . . . . . . . . . . . . 14 |- ( Iop o. Iop ) = Iop
118	117	a1i 11	. . . . . . . . . . . . 13 |- ( k e. NN -> ( Iop o. Iop ) = Iop )
119		hoico2 28616	. . . . . . . . . . . . . 14 |- ( ( F ` k ) : ~H --> ~H -> ( Iop o. ( F ` k ) ) = ( F ` k ) )
120	36, 119	syl 17	. . . . . . . . . . . . 13 |- ( k e. NN -> ( Iop o. ( F ` k ) ) = ( F ` k ) )
121	118, 120	oveq12d 6668	. . . . . . . . . . . 12 |- ( k e. NN -> ( ( Iop o. Iop ) -op ( Iop o. ( F ` k ) ) ) = ( Iop -op ( F ` k ) ) )
122	116, 121	eqtrd 2656	. . . . . . . . . . 11 |- ( k e. NN -> ( Iop o. ( Iop -op ( F ` k ) ) ) = ( Iop -op ( F ` k ) ) )
123		hmoplin 28801	. . . . . . . . . . . . . 14 |- ( ( F ` k ) e. HrmOp -> ( F ` k ) e. LinOp )
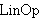124	15, 123	syl 17	. . . . . . . . . . . . 13 |- ( k e. NN -> ( F ` k ) e. LinOp )
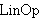125		hoddi 28849	. . . . . . . . . . . . . 14 |- ( ( ( F ` k ) e. LinOp /\ Iop : ~H --> ~H /\ ( F ` k ) : ~H --> ~H ) -> ( ( F ` k ) o. ( Iop -op ( F ` k ) ) ) = ( ( ( F ` k ) o. Iop ) -op ( ( F ` k ) o. ( F ` k ) ) ) )
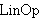
126	46, 125	mp3an2 1412	. . . . . . . . . . . . 13 |- ( ( ( F ` k ) e. LinOp /\ ( F ` k ) : ~H --> ~H ) -> ( ( F ` k ) o. ( Iop -op ( F ` k ) ) ) = ( ( ( F ` k ) o. Iop ) -op ( ( F ` k ) o. ( F ` k ) ) ) )
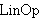127	124, 36, 126	syl2anc 693	. . . . . . . . . . . 12 |- ( k e. NN -> ( ( F ` k ) o. ( Iop -op ( F ` k ) ) ) = ( ( ( F ` k ) o. Iop ) -op ( ( F ` k ) o. ( F ` k ) ) ) )
128		hoico1 28615	. . . . . . . . . . . . . 14 |- ( ( F ` k ) : ~H --> ~H -> ( ( F ` k ) o. Iop ) = ( F ` k ) )
129	36, 128	syl 17	. . . . . . . . . . . . 13 |- ( k e. NN -> ( ( F ` k ) o. Iop ) = ( F ` k ) )
130	129	oveq1d 6665	. . . . . . . . . . . 12 |- ( k e. NN -> ( ( ( F ` k ) o. Iop ) -op ( ( F ` k ) o. ( F ` k ) ) ) = ( ( F ` k ) -op ( ( F ` k ) o. ( F ` k ) ) ) )
131	127, 130	eqtrd 2656	. . . . . . . . . . 11 |- ( k e. NN -> ( ( F ` k ) o. ( Iop -op ( F ` k ) ) ) = ( ( F ` k ) -op ( ( F ` k ) o. ( F ` k ) ) ) )
132	122, 131	oveq12d 6668	. . . . . . . . . 10 |- ( k e. NN -> ( ( Iop o. ( Iop -op ( F ` k ) ) ) -op ( ( F ` k ) o. ( Iop -op ( F ` k ) ) ) ) = ( ( Iop -op ( F ` k ) ) -op ( ( F ` k ) -op ( ( F ` k ) o. ( F ` k ) ) ) ) )
133	36, 46	jctil 560	. . . . . . . . . . 11 |- ( k e. NN -> ( Iop : ~H --> ~H /\ ( F ` k ) : ~H --> ~H ) )
134		hosubadd4 28673	. . . . . . . . . . 11 |- ( ( ( Iop : ~H --> ~H /\ ( F ` k ) : ~H --> ~H ) /\ ( ( F ` k ) : ~H --> ~H /\ ( ( F ` k ) o. ( F ` k ) ) : ~H --> ~H ) ) -> ( ( Iop -op ( F ` k ) ) -op ( ( F ` k ) -op ( ( F ` k ) o. ( F ` k ) ) ) ) = ( ( Iop +op ( ( F ` k ) o. ( F ` k ) ) ) -op ( ( F ` k ) +op ( F ` k ) ) ) )
135	133, 36, 42, 134	syl12anc 1324	. . . . . . . . . 10 |- ( k e. NN -> ( ( Iop -op ( F ` k ) ) -op ( ( F ` k ) -op ( ( F ` k ) o. ( F ` k ) ) ) ) = ( ( Iop +op ( ( F ` k ) o. ( F ` k ) ) ) -op ( ( F ` k ) +op ( F ` k ) ) ) )
136	132, 135	eqtrd 2656	. . . . . . . . 9 |- ( k e. NN -> ( ( Iop o. ( Iop -op ( F ` k ) ) ) -op ( ( F ` k ) o. ( Iop -op ( F ` k ) ) ) ) = ( ( Iop +op ( ( F ` k ) o. ( F ` k ) ) ) -op ( ( F ` k ) +op ( F ` k ) ) ) )
137		ho2times 28678	. . . . . . . . . . 11 |- ( ( F ` k ) : ~H --> ~H -> ( 2 .op ( F ` k ) ) = ( ( F ` k ) +op ( F ` k ) ) )
138	36, 137	syl 17	. . . . . . . . . 10 |- ( k e. NN -> ( 2 .op ( F ` k ) ) = ( ( F ` k ) +op ( F ` k ) ) )
139	138	oveq2d 6666	. . . . . . . . 9 |- ( k e. NN -> ( ( Iop +op ( ( F ` k ) o. ( F ` k ) ) ) -op ( 2 .op ( F ` k ) ) ) = ( ( Iop +op ( ( F ` k ) o. ( F ` k ) ) ) -op ( ( F ` k ) +op ( F ` k ) ) ) )
140		hoaddsubass 28674	. . . . . . . . . . 11 |- ( ( Iop : ~H --> ~H /\ ( ( F ` k ) o. ( F ` k ) ) : ~H --> ~H /\ ( 2 .op ( F ` k ) ) : ~H --> ~H ) -> ( ( Iop +op ( ( F ` k ) o. ( F ` k ) ) ) -op ( 2 .op ( F ` k ) ) ) = ( Iop +op ( ( ( F ` k ) o. ( F ` k ) ) -op ( 2 .op ( F ` k ) ) ) ) )
141	46, 140	mp3an1 1411	. . . . . . . . . 10 |- ( ( ( ( F ` k ) o. ( F ` k ) ) : ~H --> ~H /\ ( 2 .op ( F ` k ) ) : ~H --> ~H ) -> ( ( Iop +op ( ( F ` k ) o. ( F ` k ) ) ) -op ( 2 .op ( F ` k ) ) ) = ( Iop +op ( ( ( F ` k ) o. ( F ` k ) ) -op ( 2 .op ( F ` k ) ) ) ) )
142	42, 38, 141	syl2anc 693	. . . . . . . . 9 |- ( k e. NN -> ( ( Iop +op ( ( F ` k ) o. ( F ` k ) ) ) -op ( 2 .op ( F ` k ) ) ) = ( Iop +op ( ( ( F ` k ) o. ( F ` k ) ) -op ( 2 .op ( F ` k ) ) ) ) )
143	136, 139, 142	3eqtr2d 2662	. . . . . . . 8 |- ( k e. NN -> ( ( Iop o. ( Iop -op ( F ` k ) ) ) -op ( ( F ` k ) o. ( Iop -op ( F ` k ) ) ) ) = ( Iop +op ( ( ( F ` k ) o. ( F ` k ) ) -op ( 2 .op ( F ` k ) ) ) ) )
144	111, 143	eqtrd 2656	. . . . . . 7 |- ( k e. NN -> ( ( Iop -op ( F ` k ) ) o. ( Iop -op ( F ` k ) ) ) = ( Iop +op ( ( ( F ` k ) o. ( F ` k ) ) -op ( 2 .op ( F ` k ) ) ) ) )
145	144	oveq1d 6665	. . . . . 6 |- ( k e. NN -> ( ( ( Iop -op ( F ` k ) ) o. ( Iop -op ( F ` k ) ) ) +op ( Iop -op T ) ) = ( ( Iop +op ( ( ( F ` k ) o. ( F ` k ) ) -op ( 2 .op ( F ` k ) ) ) ) +op ( Iop -op T ) ) )
146	7, 8, 9	opsqrlem5 29003	. . . . . . . 8 |- ( k e. NN -> ( F ` ( k + 1 ) ) = ( ( F ` k ) +op ( ( 1 / 2 ) .op ( T -op ( ( F ` k ) o. ( F ` k ) ) ) ) ) )
147	146	oveq2d 6666	. . . . . . 7 |- ( k e. NN -> ( Iop -op ( F ` ( k + 1 ) ) ) = ( Iop -op ( ( F ` k ) +op ( ( 1 / 2 ) .op ( T -op ( ( F ` k ) o. ( F ` k ) ) ) ) ) ) )
148	147	oveq2d 6666	. . . . . 6 |- ( k e. NN -> ( 2 .op ( Iop -op ( F ` ( k + 1 ) ) ) ) = ( 2 .op ( Iop -op ( ( F ` k ) +op ( ( 1 / 2 ) .op ( T -op ( ( F ` k ) o. ( F ` k ) ) ) ) ) ) ) )
149	106, 145, 148	3eqtr4d 2666	. . . . 5 |- ( k e. NN -> ( ( ( Iop -op ( F ` k ) ) o. ( Iop -op ( F ` k ) ) ) +op ( Iop -op T ) ) = ( 2 .op ( Iop -op ( F ` ( k + 1 ) ) ) ) )
150	33, 149	breqtrd 4679	. . . 4 |- ( k e. NN -> 0hop <_op ( 2 .op ( Iop -op ( F ` ( k + 1 ) ) ) ) )
151		peano2nn 11032	. . . . . . 7 |- ( k e. NN -> ( k + 1 ) e. NN )
152	14	ffvelrni 6358	. . . . . . 7 |- ( ( k + 1 ) e. NN -> ( F ` ( k + 1 ) ) e. HrmOp )
153	151, 152	syl 17	. . . . . 6 |- ( k e. NN -> ( F ` ( k + 1 ) ) e. HrmOp )
154		hmopd 28881	. . . . . 6 |- ( ( Iop e. HrmOp /\ ( F ` ( k + 1 ) ) e. HrmOp ) -> ( Iop -op ( F ` ( k + 1 ) ) ) e. HrmOp )
155	13, 153, 154	sylancr 695	. . . . 5 |- ( k e. NN -> ( Iop -op ( F ` ( k + 1 ) ) ) e. HrmOp )
156		2re 11090	. . . . . 6 |- 2 e. RR
157		2pos 11112	. . . . . 6 |- 0 < 2
158		leopmul 28993	. . . . . 6 |- ( ( 2 e. RR /\ ( Iop -op ( F ` ( k + 1 ) ) ) e. HrmOp /\ 0 < 2 ) -> ( 0hop <_op ( Iop -op ( F ` ( k + 1 ) ) ) <-> 0hop <_op ( 2 .op ( Iop -op ( F ` ( k + 1 ) ) ) ) ) )
159	156, 157, 158	mp3an13 1415	. . . . 5 |- ( ( Iop -op ( F ` ( k + 1 ) ) ) e. HrmOp -> ( 0hop <_op ( Iop -op ( F ` ( k + 1 ) ) ) <-> 0hop <_op ( 2 .op ( Iop -op ( F ` ( k + 1 ) ) ) ) ) )
160	155, 159	syl 17	. . . 4 |- ( k e. NN -> ( 0hop <_op ( Iop -op ( F ` ( k + 1 ) ) ) <-> 0hop <_op ( 2 .op ( Iop -op ( F ` ( k + 1 ) ) ) ) ) )
161	150, 160	mpbird 247	. . 3 |- ( k e. NN -> 0hop <_op ( Iop -op ( F ` ( k + 1 ) ) ) )
162		leop3 28984	. . . 4 |- ( ( ( F ` ( k + 1 ) ) e. HrmOp /\ Iop e. HrmOp ) -> ( ( F ` ( k + 1 ) ) <_op Iop <-> 0hop <_op ( Iop -op ( F ` ( k + 1 ) ) ) ) )
163	153, 13, 162	sylancl 694	. . 3 |- ( k e. NN -> ( ( F ` ( k + 1 ) ) <_op Iop <-> 0hop <_op ( Iop -op ( F ` ( k + 1 ) ) ) ) )
164	161, 163	mpbird 247	. 2 |- ( k e. NN -> ( F ` ( k + 1 ) ) <_op Iop )
165	2, 4, 6, 12, 164	nn1suc 11041	1 |- ( N e. NN -> ( F ` N ) <_op Iop )

Syntax hints:   -> wi 4   <-> wb 196   /\ wa 384   = wceq 1483   e. wcel 1990   {csn 4177   class class class wbr 4653   X. cxp 5112   o. ccom 5118   -->wf 5884   ` cfv 5888  (class class class)co 6650   |-> cmpt2 6652   CCcc 9934   RRcr 9935   0cc0 9936   1c1 9937   + caddc 9939   x. cmul 9941   < clt 10074   / cdiv 10684   NNcn 11020   2c2 11070   seqcseq 12801   ~Hchil 27776   +op chos 27795   .op chot 27796   -op chod 27797   0hopch0o 27800   Iop chio 27801   LinOpclo 27804   HrmOpcho 27807   <_op cleo 27815

This theorem was proved from axioms:  ax-mp 5  ax-1 6  ax-2 7  ax-3 8  ax-gen 1722  ax-4 1737  ax-5 1839  ax-6 1888  ax-7 1935  ax-8 1992  ax-9 1999  ax-10 2019  ax-11 2034  ax-12 2047  ax-13 2246  ax-ext 2602  ax-rep 4771  ax-sep 4781  ax-nul 4789  ax-pow 4843  ax-pr 4906  ax-un 6949  ax-inf2 8538  ax-cc 9257  ax-cnex 9992  ax-resscn 9993  ax-1cn 9994  ax-icn 9995  ax-addcl 9996  ax-addrcl 9997  ax-mulcl 9998  ax-mulrcl 9999  ax-mulcom 10000  ax-addass 10001  ax-mulass 10002  ax-distr 10003  ax-i2m1 10004  ax-1ne0 10005  ax-1rid 10006  ax-rnegex 10007  ax-rrecex 10008  ax-cnre 10009  ax-pre-lttri 10010  ax-pre-lttrn 10011  ax-pre-ltadd 10012  ax-pre-mulgt0 10013  ax-pre-sup 10014  ax-addf 10015  ax-mulf 10016  ax-hilex 27856  ax-hfvadd 27857  ax-hvcom 27858  ax-hvass 27859  ax-hv0cl 27860  ax-hvaddid 27861  ax-hfvmul 27862  ax-hvmulid 27863  ax-hvmulass 27864  ax-hvdistr1 27865  ax-hvdistr2 27866  ax-hvmul0 27867  ax-hfi 27936  ax-his1 27939  ax-his2 27940  ax-his3 27941  ax-his4 27942  ax-hcompl 28059

This theorem depends on definitions:  df-bi 197  df-or 385  df-an 386  df-3or 1038  df-3an 1039  df-tru 1486  df-fal 1489  df-ex 1705  df-nf 1710  df-sb 1881  df-eu 2474  df-mo 2475  df-clab 2609  df-cleq 2615  df-clel 2618  df-nfc 2753  df-ne 2795  df-nel 2898  df-ral 2917  df-rex 2918  df-reu 2919  df-rmo 2920  df-rab 2921  df-v 3202  df-sbc 3436  df-csb 3534  df-dif 3577  df-un 3579  df-in 3581  df-ss 3588  df-pss 3590  df-nul 3916  df-if 4087  df-pw 4160  df-sn 4178  df-pr 4180  df-tp 4182  df-op 4184  df-uni 4437  df-int 4476  df-iun 4522  df-iin 4523  df-br 4654  df-opab 4713  df-mpt 4730  df-tr 4753  df-id 5024  df-eprel 5029  df-po 5035  df-so 5036  df-fr 5073  df-se 5074  df-we 5075  df-xp 5120  df-rel 5121  df-cnv 5122  df-co 5123  df-dm 5124  df-rn 5125  df-res 5126  df-ima 5127  df-pred 5680  df-ord 5726  df-on 5727  df-lim 5728  df-suc 5729  df-iota 5851  df-fun 5890  df-fn 5891  df-f 5892  df-f1 5893  df-fo 5894  df-f1o 5895  df-fv 5896  df-isom 5897  df-riota 6611  df-ov 6653  df-oprab 6654  df-mpt2 6655  df-of 6897  df-om 7066  df-1st 7168  df-2nd 7169  df-supp 7296  df-wrecs 7407  df-recs 7468  df-rdg 7506  df-1o 7560  df-2o 7561  df-oadd 7564  df-omul 7565  df-er 7742  df-map 7859  df-pm 7860  df-ixp 7909  df-en 7956  df-dom 7957  df-sdom 7958  df-fin 7959  df-fsupp 8276  df-fi 8317  df-sup 8348  df-inf 8349  df-oi 8415  df-card 8765  df-acn 8768  df-cda 8990  df-pnf 10076  df-mnf 10077  df-xr 10078  df-ltxr 10079  df-le 10080  df-sub 10268  df-neg 10269  df-div 10685  df-nn 11021  df-2 11079  df-3 11080  df-4 11081  df-5 11082  df-6 11083  df-7 11084  df-8 11085  df-9 11086  df-n0 11293  df-z 11378  df-dec 11494  df-uz 11688  df-q 11789  df-rp 11833  df-xneg 11946  df-xadd 11947  df-xmul 11948  df-ioo 12179  df-ico 12181  df-icc 12182  df-fz 12327  df-fzo 12466  df-fl 12593  df-seq 12802  df-exp 12861  df-hash 13118  df-cj 13839  df-re 13840  df-im 13841  df-sqrt 13975  df-abs 13976  df-clim 14219  df-rlim 14220  df-sum 14417  df-struct 15859  df-ndx 15860  df-slot 15861  df-base 15863  df-sets 15864  df-ress 15865  df-plusg 15954  df-mulr 15955  df-starv 15956  df-sca 15957  df-vsca 15958  df-ip 15959  df-tset 15960  df-ple 15961  df-ds 15964  df-unif 15965  df-hom 15966  df-cco 15967  df-rest 16083  df-topn 16084  df-0g 16102  df-gsum 16103  df-topgen 16104  df-pt 16105  df-prds 16108  df-xrs 16162  df-qtop 16167  df-imas 16168  df-xps 16170  df-mre 16246  df-mrc 16247  df-acs 16249  df-mgm 17242  df-sgrp 17284  df-mnd 17295  df-submnd 17336  df-mulg 17541  df-cntz 17750  df-cmn 18195  df-psmet 19738  df-xmet 19739  df-met 19740  df-bl 19741  df-mopn 19742  df-fbas 19743  df-fg 19744  df-cnfld 19747  df-top 20699  df-topon 20716  df-topsp 20737  df-bases 20750  df-cld 20823  df-ntr 20824  df-cls 20825  df-nei 20902  df-cn 21031  df-cnp 21032  df-lm 21033  df-haus 21119  df-tx 21365  df-hmeo 21558  df-fil 21650  df-fm 21742  df-flim 21743  df-flf 21744  df-xms 22125  df-ms 22126  df-tms 22127  df-cfil 23053  df-cau 23054  df-cmet 23055  df-grpo 27347  df-gid 27348  df-ginv 27349  df-gdiv 27350  df-ablo 27399  df-vc 27414  df-nv 27447  df-va 27450  df-ba 27451  df-sm 27452  df-0v 27453  df-vs 27454  df-nmcv 27455  df-ims 27456  df-dip 27556  df-ssp 27577  df-ph 27668  df-cbn 27719  df-hnorm 27825  df-hba 27826  df-hvsub 27828  df-hlim 27829  df-hcau 27830  df-sh 28064  df-ch 28078  df-oc 28109  df-ch0 28110  df-shs 28167  df-pjh 28254  df-hosum 28589  df-homul 28590  df-hodif 28591  df-h0op 28607  df-iop 28608  df-lnop 28700  df-hmop 28703  df-leop 28711

This theorem is referenced by: (None)