| Step | Hyp | Ref
| Expression |
|---|
| 1 | | smcn.u |
. . 3
    |
| 2 | | smcn.x |
. . . 4
    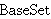    |
| 3 | | smcn.s |
. . . 4
         |
| 4 | 2, 3 | nvsf 27474 |
. . 3
                |
| 5 | 1, 4 | ax-mp 5 |
. 2
          |
| 6 | | smcn.t |
. . . . . 6
                                |
| 7 | | 1rp 11836 |
. . . . . . . 8
    |
| 8 | | simpr 477 |
. . . . . . . . . . . 12
        
       |
| 9 | | smcn.n |
. . . . . . . . . . . . 13
     CV CV   |
| 10 | 2, 9 | nvcl 27516 |
. . . . . . . . . . . 12
                    |
| 11 | 1, 8, 10 | sylancr 695 |
. . . . . . . . . . 11
        
           |
| 12 | | abscl 14018 |
. . . . . . . . . . . 12
              |
| 13 | 12 | adantr 481 |
. . . . . . . . . . 11
        
           |
| 14 | 11, 13 | readdcld 10069 |
. . . . . . . . . 10
        
                   |
| 15 | 2, 9 | nvge0 27528 |
. . . . . . . . . . . 12
                    |
| 16 | 1, 8, 15 | sylancr 695 |
. . . . . . . . . . 11
        
    
      |
| 17 | | absge0 14027 |
. . . . . . . . . . . 12
              |
| 18 | 17 | adantr 481 |
. . . . . . . . . . 11
        
    
      |
| 19 | 11, 13, 16, 18 | addge0d 10603 |
. . . . . . . . . 10
        
    
              |
| 20 | 14, 19 | ge0p1rpd 11902 |
. . . . . . . . 9
        
                       |
| 21 | | rpdivcl 11856 |
. . . . . . . . 9
                                                    |
| 22 | 20, 21 | sylan 488 |
. . . . . . . 8
                                          |
| 23 | | rpaddcl 11854 |
. . . . . . . 8
                                                            |
| 24 | 7, 22, 23 | sylancr 695 |
. . . . . . 7
                                              |
| 25 | 24 | rpreccld 11882 |
. . . . . 6
                                                  |
| 26 | 6, 25 | syl5eqel 2705 |
. . . . 5
                      |
| 27 | | smcn.c |
. . . . . . . . . . . 12
    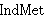    |
| 28 | 2, 27 | imsmet 27546 |
. . . . . . . . . . 11
              |
| 29 | 1, 28 | ax-mp 5 |
. . . . . . . . . 10
        |
| 30 | 29 | a1i 11 |
. . . . . . . . 9
                                          
                   |
| 31 | 1 | a1i 11 |
. . . . . . . . . 10
                                          
               |
| 32 | | simplll 798 |
. . . . . . . . . 10
                                          
               |
| 33 | | simpllr 799 |
. . . . . . . . . 10
                                          
               |
| 34 | 2, 3 | nvscl 27481 |
. . . . . . . . . 10
                        |
| 35 | 31, 32, 33, 34 | syl3anc 1326 |
. . . . . . . . 9
                                          
                   |
| 36 | | simprll 802 |
. . . . . . . . . 10
                                          
               |
| 37 | | simprlr 803 |
. . . . . . . . . 10
                                          
               |
| 38 | 2, 3 | nvscl 27481 |
. . . . . . . . . 10
                        |
| 39 | 31, 36, 37, 38 | syl3anc 1326 |
. . . . . . . . 9
                                          
                   |
| 40 | | metcl 22137 |
. . . . . . . . 9
                                            |
| 41 | 30, 35, 39, 40 | syl3anc 1326 |
. . . . . . . 8
                                          
                           |
| 42 | 2, 3 | nvscl 27481 |
. . . . . . . . . . 11
                        |
| 43 | 31, 36, 33, 42 | syl3anc 1326 |
. . . . . . . . . 10
                                          
                   |
| 44 | | metcl 22137 |
. . . . . . . . . 10
                                            |
| 45 | 30, 35, 43, 44 | syl3anc 1326 |
. . . . . . . . 9
                                          
                           |
| 46 | | metcl 22137 |
. . . . . . . . . 10
                                            |
| 47 | 30, 43, 39, 46 | syl3anc 1326 |
. . . . . . . . 9
                                          
                           |
| 48 | 45, 47 | readdcld 10069 |
. . . . . . . 8
                                          
                                           |
| 49 | | rpre 11839 |
. . . . . . . . 9
    
     |
| 50 | 49 | ad2antlr 763 |
. . . . . . . 8
                                          
               |
| 51 | | mettri 22157 |
. . . . . . . . 9
                                     
                                            |
| 52 | 30, 35, 39, 43, 51 | syl13anc 1328 |
. . . . . . . 8
                                          
                                                       |
| 53 | 1, 33, 10 | sylancr 695 |
. . . . . . . . . . . 12
                                          
                   |
| 54 | 32 | abscld 14175 |
. . . . . . . . . . . 12
                                          
                   |
| 55 | 53, 54 | readdcld 10069 |
. . . . . . . . . . 11
                                          
                           |
| 56 | | peano2re 10209 |
. . . . . . . . . . 11
                 
                    |
| 57 | 55, 56 | syl 17 |
. . . . . . . . . 10
                                          
                               |
| 58 | 26 | adantr 481 |
. . . . . . . . . . 11
                                          
               |
| 59 | 58 | rpred 11872 |
. . . . . . . . . 10
                                          
               |
| 60 | 57, 59 | remulcld 10070 |
. . . . . . . . 9
                                          
                                   |
| 61 | 32, 36 | subcld 10392 |
. . . . . . . . . . . . 13
                                          
                   |
| 62 | 61 | abscld 14175 |
. . . . . . . . . . . 12
                                          
                       |
| 63 | 62, 53 | remulcld 10070 |
. . . . . . . . . . 11
                                          
                               |
| 64 | 36 | abscld 14175 |
. . . . . . . . . . . 12
                                          
                   |
| 65 | | eqid 2622 |
. . . . . . . . . . . . . . 15
            |
| 66 | 2, 65 | nvmcl 27501 |
. . . . . . . . . . . . . 14
         
                  |
| 67 | 31, 33, 37, 66 | syl3anc 1326 |
. . . . . . . . . . . . 13
                                          
                       |
| 68 | 2, 9 | nvcl 27516 |
. . . . . . . . . . . . 13
                                    |
| 69 | 1, 67, 68 | sylancr 695 |
. . . . . . . . . . . 12
                                          
                           |
| 70 | 64, 69 | remulcld 10070 |
. . . . . . . . . . 11
                                          
                                   |
| 71 | 53, 59 | remulcld 10070 |
. . . . . . . . . . 11
                                          
                       |
| 72 | | peano2re 10209 |
. . . . . . . . . . . . 13
                      |
| 73 | 54, 72 | syl 17 |
. . . . . . . . . . . 12
                                          
                       |
| 74 | 73, 59 | remulcld 10070 |
. . . . . . . . . . 11
                                          
                           |
| 75 | 1, 33, 15 | sylancr 695 |
. . . . . . . . . . . . 13
                                          
                   |
| 76 | 32, 36 | abssubd 14192 |
. . . . . . . . . . . . . 14
                                          
                               |
| 77 | 36, 32 | subcld 10392 |
. . . . . . . . . . . . . . . 16
                                          
                   |
| 78 | 77 | abscld 14175 |
. . . . . . . . . . . . . . 15
                                          
                       |
| 79 | | eqid 2622 |
. . . . . . . . . . . . . . . . . . 19
    
       |
| 80 | 79 | cnmetdval 22574 |
. . . . . . . . . . . . . . . . . 18
        
        
              |
| 81 | 32, 36, 80 | syl2anc 693 |
. . . . . . . . . . . . . . . . 17
                                          
                               |
| 82 | 81, 76 | eqtrd 2656 |
. . . . . . . . . . . . . . . 16
                                          
                               |
| 83 | | simprrl 804 |
. . . . . . . . . . . . . . . 16
                                          
                       |
| 84 | 82, 83 | eqbrtrrd 4677 |
. . . . . . . . . . . . . . 15
                                          
                       |
| 85 | 78, 59, 84 | ltled 10185 |
. . . . . . . . . . . . . 14
                                          
                    
  |
| 86 | 76, 85 | eqbrtrd 4675 |
. . . . . . . . . . . . 13
                                          
                    
  |
| 87 | 62, 59, 53, 75, 86 | lemul1ad 10963 |
. . . . . . . . . . . 12
                                          
                            
          |
| 88 | 58 | rpcnd 11874 |
. . . . . . . . . . . . 13
                                          
               |
| 89 | 53 | recnd 10068 |
. . . . . . . . . . . . 13
                                          
                   |
| 90 | 88, 89 | mulcomd 10061 |
. . . . . . . . . . . 12
                                          
                               |
| 91 | 87, 90 | breqtrd 4679 |
. . . . . . . . . . 11
                                          
                            
          |
| 92 | 36 | absge0d 14183 |
. . . . . . . . . . . 12
                                          
                   |
| 93 | 2, 9 | nvge0 27528 |
. . . . . . . . . . . . 13
                     
              |
| 94 | 1, 67, 93 | sylancr 695 |
. . . . . . . . . . . 12
                                          
                           |
| 95 | 54, 78 | readdcld 10069 |
. . . . . . . . . . . . 13
                                          
                               |
| 96 | 32, 36 | pncan3d 10395 |
. . . . . . . . . . . . . . 15
                                          
                       |
| 97 | 96 | fveq2d 6195 |
. . . . . . . . . . . . . 14
                                          
                               |
| 98 | 32, 77 | abstrid 14195 |
. . . . . . . . . . . . . 14
                                          
                        
                  |
| 99 | 97, 98 | eqbrtrrd 4677 |
. . . . . . . . . . . . 13
                                          
                
                  |
| 100 | | 1red 10055 |
. . . . . . . . . . . . . 14
                                          
               |
| 101 | | 1re 10039 |
. . . . . . . . . . . . . . . . . . 19
    |
| 102 | 22 | adantr 481 |
. . . . . . . . . . . . . . . . . . 19
                                          
                                   |
| 103 | | ltaddrp 11867 |
. . . . . . . . . . . . . . . . . . 19
                                                            |
| 104 | 101, 102,
103 | sylancr 695 |
. . . . . . . . . . . . . . . . . 18
                                          
                                       |
| 105 | 24 | adantr 481 |
. . . . . . . . . . . . . . . . . . 19
                                          
                                       |
| 106 | 105 | recgt1d 11886 |
. . . . . . . . . . . . . . . . . 18
                                          
                                                                         |
| 107 | 104, 106 | mpbid 222 |
. . . . . . . . . . . . . . . . 17
                                          
                                           |
| 108 | 6, 107 | syl5eqbr 4688 |
. . . . . . . . . . . . . . . 16
                                          
               |
| 109 | 59, 100, 108 | ltled 10185 |
. . . . . . . . . . . . . . 15
                                          
               |
| 110 | 78, 59, 100, 85, 109 | letrd 10194 |
. . . . . . . . . . . . . 14
                                          
                    
  |
| 111 | 78, 100, 54, 110 | leadd2dd 10642 |
. . . . . . . . . . . . 13
                                          
                            
          |
| 112 | 64, 95, 73, 99, 111 | letrd 10194 |
. . . . . . . . . . . 12
                                          
                
          |
| 113 | 2, 65, 9, 27 | imsdval 27541 |
. . . . . . . . . . . . . . 15
         
                          |
| 114 | 31, 33, 37, 113 | syl3anc 1326 |
. . . . . . . . . . . . . 14
                                          
                               |
| 115 | | simprrr 805 |
. . . . . . . . . . . . . 14
                                          
                   |
| 116 | 114, 115 | eqbrtrrd 4677 |
. . . . . . . . . . . . 13
                                          
                           |
| 117 | 69, 59, 116 | ltled 10185 |
. . . . . . . . . . . 12
                                          
                           |
| 118 | 64, 73, 69, 59, 92, 94, 112, 117 | lemul12ad 10966 |
. . . . . . . . . . 11
                                          
                                
              |
| 119 | 63, 70, 71, 74, 91, 118 | le2addd 10646 |
. . . . . . . . . 10
                                          
                                                    
                          |
| 120 | | eqid 2622 |
. . . . . . . . . . . . . 14
            |
| 121 | 2, 120, 3, 9, 27 | imsdval2 27542 |
. . . . . . . . . . . . 13
                                                                 |
| 122 | 31, 35, 43, 121 | syl3anc 1326 |
. . . . . . . . . . . 12
                                          
                                                    |
| 123 | | neg1cn 11124 |
. . . . . . . . . . . . . . . 16
     |
| 124 | | mulcl 10020 |
. . . . . . . . . . . . . . . 16
                      |
| 125 | 123, 36, 124 | sylancr 695 |
. . . . . . . . . . . . . . 15
                                          
                    |
| 126 | 2, 120, 3 | nvdir 27486 |
. . . . . . . . . . . . . . 15
                      
   
                                      |
| 127 | 31, 32, 125, 33, 126 | syl13anc 1328 |
. . . . . . . . . . . . . 14
                                          
                                                 |
| 128 | 36 | mulm1d 10482 |
. . . . . . . . . . . . . . . . 17
                                          
                     |
| 129 | 128 | oveq2d 6666 |
. . . . . . . . . . . . . . . 16
                                          
                             |
| 130 | 32, 36 | negsubd 10398 |
. . . . . . . . . . . . . . . 16
                                          
                        |
| 131 | 129, 130 | eqtrd 2656 |
. . . . . . . . . . . . . . 15
                                          
                            |
| 132 | 131 | oveq1d 6665 |
. . . . . . . . . . . . . 14
                                          
                                    |
| 133 | 123 | a1i 11 |
. . . . . . . . . . . . . . . 16
                                          
                |
| 134 | 2, 3 | nvsass 27483 |
. . . . . . . . . . . . . . . 16
              
                              |
| 135 | 31, 133, 36, 33, 134 | syl13anc 1328 |
. . . . . . . . . . . . . . 15
                                          
                                 |
| 136 | 135 | oveq2d 6666 |
. . . . . . . . . . . . . 14
                                          
                                                         |
| 137 | 127, 132,
136 | 3eqtr3d 2664 |
. . . . . . . . . . . . 13
                                          
                                            |
| 138 | 137 | fveq2d 6195 |
. . . . . . . . . . . 12
                                          
                                                    |
| 139 | 2, 3, 9 | nvs 27518 |
. . . . . . . . . . . . 13
                                                    |
| 140 | 31, 61, 33, 139 | syl3anc 1326 |
. . . . . . . . . . . 12
                                          
                                           |
| 141 | 122, 138,
140 | 3eqtr2d 2662 |
. . . . . . . . . . 11
                                          
                                           |
| 142 | 2, 65, 9, 27 | imsdval 27541 |
. . . . . . . . . . . . 13
                                                            |
| 143 | 31, 43, 39, 142 | syl3anc 1326 |
. . . . . . . . . . . 12
                                          
                                               |
| 144 | 2, 65, 3 | nvmdi 27503 |
. . . . . . . . . . . . . 14
             
   
   
                                |
| 145 | 31, 36, 33, 37, 144 | syl13anc 1328 |
. . . . . . . . . . . . 13
                                          
                                           |
| 146 | 145 | fveq2d 6195 |
. . . . . . . . . . . 12
                                          
                                                   |
| 147 | 2, 3, 9 | nvs 27518 |
. . . . . . . . . . . . 13
                                                                |
| 148 | 31, 36, 67, 147 | syl3anc 1326 |
. . . . . . . . . . . 12
                                          
                                                   |
| 149 | 143, 146,
148 | 3eqtr2d 2662 |
. . . . . . . . . . 11
                                          
                                               |
| 150 | 141, 149 | oveq12d 6668 |
. . . . . . . . . 10
                                          
                                                                                   |
| 151 | 54 | recnd 10068 |
. . . . . . . . . . . . 13
                                          
                   |
| 152 | | 1cnd 10056 |
. . . . . . . . . . . . 13
                                          
               |
| 153 | 89, 151, 152 | addassd 10062 |
. . . . . . . . . . . 12
                                          
                                               |
| 154 | 153 | oveq1d 6665 |
. . . . . . . . . . 11
                                          
                                                       |
| 155 | 73 | recnd 10068 |
. . . . . . . . . . . 12
                                          
                       |
| 156 | 89, 155, 88 | adddird 10065 |
. . . . . . . . . . 11
                                          
                                                           |
| 157 | 154, 156 | eqtrd 2656 |
. . . . . . . . . 10
                                          
                                                           |
| 158 | 119, 150,
157 | 3brtr4d 4685 |
. . . . . . . . 9
                                          
                                                               |
| 159 | 57 | recnd 10068 |
. . . . . . . . . . . 12
                                          
                               |
| 160 | 105 | rpcnd 11874 |
. . . . . . . . . . . 12
                                          
                                       |
| 161 | 105 | rpne0d 11877 |
. . . . . . . . . . . 12
                                          
                                       |
| 162 | 159, 160,
161 | divrecd 10804 |
. . . . . . . . . . 11
                                          
                                                                                                           |
| 163 | 6 | oveq2i 6661 |
. . . . . . . . . . 11
                                                                        |
| 164 | 162, 163 | syl6reqr 2675 |
. . . . . . . . . 10
                                          
                                                                               |
| 165 | | simplr 792 |
. . . . . . . . . . 11
                                          
               |
| 166 | 102 | rpred 11872 |
. . . . . . . . . . . . 13
                                          
                                   |
| 167 | 166 | ltp1d 10954 |
. . . . . . . . . . . 12
                                          
                                
                          |
| 168 | 102 | rpcnd 11874 |
. . . . . . . . . . . . 13
                                          
                                   |
| 169 | 168, 152 | addcomd 10238 |
. . . . . . . . . . . 12
                                          
                                                               |
| 170 | 167, 169 | breqtrd 4679 |
. . . . . . . . . . 11
                                          
                                
                          |
| 171 | 57, 165, 105, 170 | ltdiv23d 11937 |
. . . . . . . . . 10
                                          
                                                           |
| 172 | 164, 171 | eqbrtrd 4675 |
. . . . . . . . 9
                                          
                                
  |
| 173 | 48, 60, 50, 158, 172 | lelttrd 10195 |
. . . . . . . 8
                                          
                                           |
| 174 | 41, 48, 50, 52, 173 | lelttrd 10195 |
. . . . . . 7
                                          
                           |
| 175 | 174 | expr 643 |
. . . . . 6
                         
   
       
   
                            |
| 176 | 175 | ralrimivva 2971 |
. . . . 5
                                                                  |
| 177 | | breq2 4657 |
. . . . . . . . 9
            
   
 
   
         |
| 178 | | breq2 4657 |
. . . . . . . . 9
              
         |
| 179 | 177, 178 | anbi12d 747 |
. . . . . . . 8
                                                    |
| 180 | 179 | imbi1d 331 |
. . . . . . 7
                    
                         
       
   
                             |
| 181 | 180 | 2ralbidv 2989 |
. . . . . 6
        
                                                                                               |
| 182 | 181 | rspcev 3309 |
. . . . 5
         
    
       
   
                                                                                 |
| 183 | 26, 176, 182 | syl2anc 693 |
. . . 4
                            
                                         |
| 184 | 183 | ralrimiva 2966 |
. . 3
        
                                                           |
| 185 | 184 | rgen2 2975 |
. 2
                       
                                        |
| 186 | | cnxmet 22576 |
. . 3
    
        |
| 187 | 2, 27 | imsxmet 27547 |
. . . 4
               |
| 188 | 1, 187 | ax-mp 5 |
. . 3
         |
| 189 | | smcn.k |
. . . . 5
      ℂfld ℂfld |
| 190 | 189 | cnfldtopn 22585 |
. . . 4
            |
| 191 | | smcn.j |
. . . 4
        |
| 192 | 190, 191,
191 | txmetcn 22353 |
. . 3
        
        
        
                                  
    
                                                          |
| 193 | 186, 188,
188, 192 | mp3an 1424 |
. 2
             
                 
   
                                                      |
| 194 | 5, 185, 193 | mpbir2an 955 |
1
            |