poimirlem30 - Mathbox for Brendan Leahy

	Mathbox for Brendan Leahy		< Previous Next > Nearby theorems
Mirrors > Home > MPE Home > Th. List > Mathboxes > poimirlem30		Structured version Visualization version Unicode version

Theorem poimirlem30 33439

Description: Lemma for poimir 33442 combining poimirlem29 33438 with bwth 21213. (Contributed by Brendan Leahy, 21-Aug-2020.)

**Hypotheses**
Ref	Expression
poimir.0
poimir.i
poimir.r
poimir.1	↾_t
poimirlem30.x
poimirlem30.2
poimirlem30.3	$/\$ ..^
poimirlem30.4	$/\$ $/\$ $/\$

**Assertion**
Ref	Expression
poimirlem30	↾_t

Distinct variable groups:

Allowed substitution hints:

(

)

(

)

Proof of Theorem poimirlem30 Dummy variables

are mutually distinct and distinct from all other variables.

Step	Hyp	Ref	Expression
1		elfzonn0 12512	. . . . . . . . . . . . . . . 16 ..^
2	1	nn0red 11352	. . . . . . . . . . . . . . 15 ..^
3		nndivre 11056	. . . . . . . . . . . . . . 15 $/\$
4	2, 3	sylan 488	. . . . . . . . . . . . . 14 ..^ $/\$
5		elfzole1 12478	. . . . . . . . . . . . . . . 16 ..^
6	2, 5	jca 554	. . . . . . . . . . . . . . 15 ..^ $/\$
7		nnrp 11842	. . . . . . . . . . . . . . . 16
8	7	rpregt0d 11878	. . . . . . . . . . . . . . 15 $/\$
9		divge0 10892	. . . . . . . . . . . . . . 15 $/\$ $/\$ $/\$
10	6, 8, 9	syl2an 494	. . . . . . . . . . . . . 14 ..^ $/\$
11		elfzo0le 12511	. . . . . . . . . . . . . . . 16 ..^
12	11	adantr 481	. . . . . . . . . . . . . . 15 ..^ $/\$
13	2	adantr 481	. . . . . . . . . . . . . . . . 17 ..^ $/\$
14		1red 10055	. . . . . . . . . . . . . . . . 17 ..^ $/\$
15	7	adantl 482	. . . . . . . . . . . . . . . . 17 ..^ $/\$
16	13, 14, 15	ledivmuld 11925	. . . . . . . . . . . . . . . 16 ..^ $/\$
17		nncn 11028	. . . . . . . . . . . . . . . . . . 19
18	17	mulid1d 10057	. . . . . . . . . . . . . . . . . 18
19	18	breq2d 4665	. . . . . . . . . . . . . . . . 17
20	19	adantl 482	. . . . . . . . . . . . . . . 16 ..^ $/\$
21	16, 20	bitrd 268	. . . . . . . . . . . . . . 15 ..^ $/\$
22	12, 21	mpbird 247	. . . . . . . . . . . . . 14 ..^ $/\$
23		0re 10040	. . . . . . . . . . . . . . 15
24		1re 10039	. . . . . . . . . . . . . . 15
25	23, 24	elicc2i 12239	. . . . . . . . . . . . . 14 $/\$ $/\$
26	4, 10, 22, 25	syl3anbrc 1246	. . . . . . . . . . . . 13 ..^ $/\$
27	26	ancoms 469	. . . . . . . . . . . 12 $/\$ ..^
28		elsni 4194	. . . . . . . . . . . . . 14
29	28	oveq2d 6666	. . . . . . . . . . . . 13
30	29	eleq1d 2686	. . . . . . . . . . . 12
31	27, 30	syl5ibrcom 237	. . . . . . . . . . 11 $/\$ ..^
32	31	impr 649	. . . . . . . . . 10 $/\$ ..^ $/\$
33	32	adantll 750	. . . . . . . . 9 $/\$ $/\$ ..^ $/\$
34		poimirlem30.2	. . . . . . . . . . . 12
35	34	ffvelrnda 6359	. . . . . . . . . . 11 $/\$
36		xp1st 7198	. . . . . . . . . . 11
37		elmapfn 7880	. . . . . . . . . . 11
38	35, 36, 37	3syl 18	. . . . . . . . . 10 $/\$
39		poimirlem30.3	. . . . . . . . . 10 $/\$ ..^
40		df-f 5892	. . . . . . . . . 10 ..^ $/\$ ..^
41	38, 39, 40	sylanbrc 698	. . . . . . . . 9 $/\$ ..^
42		vex 3203	. . . . . . . . . . 11
43	42	fconst 6091	. . . . . . . . . 10
44	43	a1i 11	. . . . . . . . 9 $/\$
45		fzfid 12772	. . . . . . . . 9 $/\$
46		inidm 3822	. . . . . . . . 9
47	33, 41, 44, 45, 45, 46	off 6912	. . . . . . . 8 $/\$
48		poimir.i	. . . . . . . . . 10
49	48	eleq2i 2693	. . . . . . . . 9
50		ovex 6678	. . . . . . . . . 10
51		ovex 6678	. . . . . . . . . 10
52	50, 51	elmap 7886	. . . . . . . . 9
53	49, 52	bitri 264	. . . . . . . 8
54	47, 53	sylibr 224	. . . . . . 7 $/\$
55		eqid 2622	. . . . . . 7
56	54, 55	fmptd 6385	. . . . . 6
57		frn 6053	. . . . . 6
58	56, 57	syl 17	. . . . 5
59		ominf 8172	. . . . . . 7
60		nnenom 12779	. . . . . . . . 9
61		enfi 8176	. . . . . . . . 9
62	60, 61	ax-mp 5	. . . . . . . 8
63		iunid 4575	. . . . . . . . . . 11
64	63	imaeq2i 5464	. . . . . . . . . 10
65		imaiun 6503	. . . . . . . . . 10
66		ovex 6678	. . . . . . . . . . . . 13
67	66, 55	fnmpti 6022	. . . . . . . . . . . 12
68		dffn3 6054	. . . . . . . . . . . 12
69	67, 68	mpbi 220	. . . . . . . . . . 11
70		fimacnv 6347	. . . . . . . . . . 11
71	69, 70	ax-mp 5	. . . . . . . . . 10
72	64, 65, 71	3eqtr3ri 2653	. . . . . . . . 9
73	72	eleq1i 2692	. . . . . . . 8
74	62, 73	bitr3i 266	. . . . . . 7
75	59, 74	mtbi 312	. . . . . 6
76		ralnex 2992	. . . . . . . . . . . 12
77	76	rexbii 3041	. . . . . . . . . . 11
78		rexnal 2995	. . . . . . . . . . 11
79	77, 78	bitri 264	. . . . . . . . . 10
80	79	ralbii 2980	. . . . . . . . 9
81		ralnex 2992	. . . . . . . . 9
82	80, 81	bitri 264	. . . . . . . 8
83		nnuz 11723	. . . . . . . . . . . . . . . 16
84		elnnuz 11724	. . . . . . . . . . . . . . . . 17
85		fzouzsplit 12503	. . . . . . . . . . . . . . . . 17 ..^
86	84, 85	sylbi 207	. . . . . . . . . . . . . . . 16 ..^
87	83, 86	syl5eq 2668	. . . . . . . . . . . . . . 15 ..^
88	87	difeq1d 3727	. . . . . . . . . . . . . 14 $\$ ..^ ..^ $\$ ..^
89		uncom 3757	. . . . . . . . . . . . . . . 16 ..^ ..^
90	89	difeq1i 3724	. . . . . . . . . . . . . . 15 ..^ $\$ ..^ ..^ $\$ ..^
91		difun2 4048	. . . . . . . . . . . . . . 15 ..^ $\$ ..^ $\$ ..^
92	90, 91	eqtri 2644	. . . . . . . . . . . . . 14 ..^ $\$ ..^ $\$ ..^
93	88, 92	syl6eq 2672	. . . . . . . . . . . . 13 $\$ ..^ $\$ ..^
94		difss 3737	. . . . . . . . . . . . 13 $\$ ..^
95	93, 94	syl6eqss 3655	. . . . . . . . . . . 12 $\$ ..^
96		ssralv 3666	. . . . . . . . . . . 12 $\$ ..^ $\$ ..^
97	95, 96	syl 17	. . . . . . . . . . 11 $\$ ..^
98		impexp 462	. . . . . . . . . . . . . . 15 $/\$ ..^ ..^
99		eldif 3584	. . . . . . . . . . . . . . . 16 $\$ ..^ $/\$ ..^
100	99	imbi1i 339	. . . . . . . . . . . . . . 15 $\$ ..^ $/\$ ..^
101		con34b 306	. . . . . . . . . . . . . . . 16 ..^ ..^
102	101	imbi2i 326	. . . . . . . . . . . . . . 15 ..^ ..^
103	98, 100, 102	3bitr4i 292	. . . . . . . . . . . . . 14 $\$ ..^ ..^
104	103	albii 1747	. . . . . . . . . . . . 13 $\$ ..^ ..^
105		df-ral 2917	. . . . . . . . . . . . 13 $\$ ..^ $\$ ..^
106		vex 3203	. . . . . . . . . . . . . . . 16
107	55	mptiniseg 5629	. . . . . . . . . . . . . . . 16
108	106, 107	ax-mp 5	. . . . . . . . . . . . . . 15
109	108	sseq1i 3629	. . . . . . . . . . . . . 14 ..^ ..^
110		rabss 3679	. . . . . . . . . . . . . 14 ..^ ..^
111		df-ral 2917	. . . . . . . . . . . . . 14 ..^ ..^
112	109, 110, 111	3bitri 286	. . . . . . . . . . . . 13 ..^ ..^
113	104, 105, 112	3bitr4i 292	. . . . . . . . . . . 12 $\$ ..^ ..^
114		fzofi 12773	. . . . . . . . . . . . 13 ..^
115		ssfi 8180	. . . . . . . . . . . . 13 ..^ $/\$ ..^
116	114, 115	mpan 706	. . . . . . . . . . . 12 ..^
117	113, 116	sylbi 207	. . . . . . . . . . 11 $\$ ..^
118	97, 117	syl6 35	. . . . . . . . . 10
119	118	rexlimiv 3027	. . . . . . . . 9
120	119	ralimi 2952	. . . . . . . 8
121	82, 120	sylbir 225	. . . . . . 7
122		iunfi 8254	. . . . . . . 8 $/\$
123	122	ex 450	. . . . . . 7
124	121, 123	syl5 34	. . . . . 6
125	75, 124	mt3i 141	. . . . 5
126		ssrexv 3667	. . . . 5
127	58, 125, 126	syl2im 40	. . . 4
128		unitssre 12319	. . . . . . . . . . . 12
129		elmapi 7879	. . . . . . . . . . . . . 14
130	129, 48	eleq2s 2719	. . . . . . . . . . . . 13
131	130	ffvelrnda 6359	. . . . . . . . . . . 12 $/\$
132	128, 131	sseldi 3601	. . . . . . . . . . 11 $/\$
133		nnrp 11842	. . . . . . . . . . . 12
134	133	rpreccld 11882	. . . . . . . . . . 11
135		eqid 2622	. . . . . . . . . . . . 13
136	135	rexmet 22594	. . . . . . . . . . . 12
137		blcntr 22218	. . . . . . . . . . . 12 $/\$ $/\$
138	136, 137	mp3an1 1411	. . . . . . . . . . 11 $/\$
139	132, 134, 138	syl2an 494	. . . . . . . . . 10 $/\$ $/\$
140	139	an32s 846	. . . . . . . . 9 $/\$ $/\$
141		fveq1 6190	. . . . . . . . . 10
142	141	eleq1d 2686	. . . . . . . . 9
143	140, 142	syl5ibrcom 237	. . . . . . . 8 $/\$ $/\$
144	143	ralrimdva 2969	. . . . . . 7 $/\$
145	144	reximdv 3016	. . . . . 6 $/\$
146	145	ralimdva 2962	. . . . 5
147	146	reximia 3009	. . . 4
148	127, 147	syl6 35	. . 3
149		poimir.r	. . . . . . . 8
150	51, 50	ixpconst 7918	. . . . . . . . 9
151	48, 150	eqtr4i 2647	. . . . . . . 8
152	149, 151	oveq12i 6662	. . . . . . 7 ↾_t ↾_t
153		fzfid 12772	. . . . . . . . 9
154		retop 22565	. . . . . . . . . . 11
155	154	fconst6 6095	. . . . . . . . . 10
156	155	a1i 11	. . . . . . . . 9
157	50	a1i 11	. . . . . . . . 9 $/\$
158	153, 156, 157	ptrest 33408	. . . . . . . 8 ↾_t ↾_t
159	158	trud 1493	. . . . . . 7 ↾_t ↾_t
160		fvex 6201	. . . . . . . . . . . 12
161	160	fvconst2 6469	. . . . . . . . . . 11
162	161	oveq1d 6665	. . . . . . . . . 10 ↾_t ↾_t
163	162	mpteq2ia 4740	. . . . . . . . 9 ↾_t ↾_t
164		fconstmpt 5163	. . . . . . . . 9 ↾_t ↾_t
165	163, 164	eqtr4i 2647	. . . . . . . 8 ↾_t ↾_t
166	165	fveq2i 6194	. . . . . . 7 ↾_t ↾_t
167	152, 159, 166	3eqtri 2648	. . . . . 6 ↾_t ↾_t
168		fzfi 12771	. . . . . . 7
169		dfii2 22685	. . . . . . . . 9 ↾_t
170		iicmp 22689	. . . . . . . . 9
171	169, 170	eqeltrri 2698	. . . . . . . 8 ↾_t
172	171	fconst6 6095	. . . . . . 7 ↾_t
173		ptcmpfi 21616	. . . . . . 7 $/\$ ↾_t ↾_t
174	168, 172, 173	mp2an 708	. . . . . 6 ↾_t
175	167, 174	eqeltri 2697	. . . . 5 ↾_t
176		rehaus 22602	. . . . . . . . . . . 12
177	176	fconst6 6095	. . . . . . . . . . 11
178		pthaus 21441	. . . . . . . . . . 11 $/\$
179	168, 177, 178	mp2an 708	. . . . . . . . . 10
180	149, 179	eqeltri 2697	. . . . . . . . 9
181		haustop 21135	. . . . . . . . 9
182	180, 181	ax-mp 5	. . . . . . . 8
183		reex 10027	. . . . . . . . . 10
184		mapss 7900	. . . . . . . . . 10 $/\$
185	183, 128, 184	mp2an 708	. . . . . . . . 9
186	48, 185	eqsstri 3635	. . . . . . . 8
187		uniretop 22566	. . . . . . . . . . 11
188	149, 187	ptuniconst 21401	. . . . . . . . . 10 $/\$
189	168, 154, 188	mp2an 708	. . . . . . . . 9
190	189	restuni 20966	. . . . . . . 8 $/\$ ↾_t
191	182, 186, 190	mp2an 708	. . . . . . 7 ↾_t
192	191	bwth 21213	. . . . . 6 ↾_t $/\$ $/\$ ↾_t
193	192	3expia 1267	. . . . 5 ↾_t $/\$ ↾_t
194	175, 58, 193	sylancr 695	. . . 4 ↾_t
195		cmptop 21198	. . . . . . . . 9 ↾_t ↾_t
196	175, 195	ax-mp 5	. . . . . . . 8 ↾_t
197	191	islp3 20950	. . . . . . . 8 ↾_t $/\$ $/\$ ↾_t ↾_t $\$
198	196, 197	mp3an1 1411	. . . . . . 7 $/\$ ↾_t ↾_t $\$
199	58, 198	sylan 488	. . . . . 6 $/\$ ↾_t ↾_t $\$
200		fzfid 12772	. . . . . . . . . . . . 13 $/\$
201	155	a1i 11	. . . . . . . . . . . . 13 $/\$
202		nnrecre 11057	. . . . . . . . . . . . . . . . 17
203	202	rexrd 10089	. . . . . . . . . . . . . . . 16
204		eqid 2622	. . . . . . . . . . . . . . . . . . 19
205	135, 204	tgioo 22599	. . . . . . . . . . . . . . . . . 18
206	205	blopn 22305	. . . . . . . . . . . . . . . . 17 $/\$ $/\$
207	136, 206	mp3an1 1411	. . . . . . . . . . . . . . . 16 $/\$
208	132, 203, 207	syl2an 494	. . . . . . . . . . . . . . 15 $/\$ $/\$
209	208	an32s 846	. . . . . . . . . . . . . 14 $/\$ $/\$
210	160	fvconst2 6469	. . . . . . . . . . . . . . 15
211	210	adantl 482	. . . . . . . . . . . . . 14 $/\$ $/\$
212	209, 211	eleqtrrd 2704	. . . . . . . . . . . . 13 $/\$ $/\$
213		noel 3919	. . . . . . . . . . . . . . . 16
214		difid 3948	. . . . . . . . . . . . . . . . 17 $\$
215	214	eleq2i 2693	. . . . . . . . . . . . . . . 16 $\$
216	213, 215	mtbir 313	. . . . . . . . . . . . . . 15 $\$
217	216	pm2.21i 116	. . . . . . . . . . . . . 14 $\$
218	217	adantl 482	. . . . . . . . . . . . 13 $/\$ $/\$ $\$
219	200, 201, 200, 212, 218	ptopn 21386	. . . . . . . . . . . 12 $/\$
220	219, 149	syl6eleqr 2712	. . . . . . . . . . 11 $/\$
221		ovex 6678	. . . . . . . . . . . . 13
222	48, 221	eqeltri 2697	. . . . . . . . . . . 12
223		elrestr 16089	. . . . . . . . . . . 12 $/\$ $/\$ ↾_t
224	180, 222, 223	mp3an12 1414	. . . . . . . . . . 11 ↾_t
225	220, 224	syl 17	. . . . . . . . . 10 $/\$ ↾_t
226		difss 3737	. . . . . . . . . . . . 13 ..^ $\$ ..^
227		imassrn 5477	. . . . . . . . . . . . 13 ..^
228	226, 227	sstri 3612	. . . . . . . . . . . 12 ..^ $\$
229	228, 58	syl5ss 3614	. . . . . . . . . . 11 ..^ $\$
230		haust1 21156	. . . . . . . . . . . . . 14
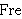231	180, 230	ax-mp 5	. . . . . . . . . . . . 13
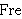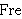
232		restt1 21171	. . . . . . . . . . . . 13 $/\$ ↾_t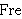
233	231, 222, 232	mp2an 708	. . . . . . . . . . . 12 ↾_t
234		funmpt 5926	. . . . . . . . . . . . . 14
235		imafi 8259	. . . . . . . . . . . . . 14 $/\$ ..^ ..^
236	234, 114, 235	mp2an 708	. . . . . . . . . . . . 13 ..^
237		diffi 8192	. . . . . . . . . . . . 13 ..^ ..^ $\$
238	236, 237	ax-mp 5	. . . . . . . . . . . 12 ..^ $\$
239	191	t1ficld 21131	. . . . . . . . . . . 12 ↾_t $/\$ ..^ $\$ $/\$ ..^ $\$ ..^ $\$ ↾_t
240	233, 238, 239	mp3an13 1415	. . . . . . . . . . 11 ..^ $\$ ..^ $\$ ↾_t
241	229, 240	syl 17	. . . . . . . . . 10 ..^ $\$ ↾_t
242	191	difopn 20838	. . . . . . . . . 10 ↾_t $/\$ ..^ $\$ ↾_t $\$ ..^ $\$ ↾_t
243	225, 241, 242	syl2anr 495	. . . . . . . . 9 $/\$ $/\$ $\$ ..^ $\$ ↾_t
244	243	anassrs 680	. . . . . . . 8 $/\$ $/\$ $\$ ..^ $\$ ↾_t
245		eleq2 2690	. . . . . . . . . . 11 $\$ ..^ $\$ $\$ ..^ $\$
246		ineq1 3807	. . . . . . . . . . . 12 $\$ ..^ $\$ $\$ $\$ ..^ $\$ $\$
247	246	neeq1d 2853	. . . . . . . . . . 11 $\$ ..^ $\$ $\$ $\$ ..^ $\$ $\$
248	245, 247	imbi12d 334	. . . . . . . . . 10 $\$ ..^ $\$ $\$ $\$ ..^ $\$ $\$ ..^ $\$ $\$
249	248	rspcva 3307	. . . . . . . . 9 $\$ ..^ $\$ ↾_t $/\$ ↾_t $\$ $\$ ..^ $\$ $\$ ..^ $\$ $\$
250		ffn 6045	. . . . . . . . . . . . . . . 16
251	130, 250	syl 17	. . . . . . . . . . . . . . 15
252	251	adantr 481	. . . . . . . . . . . . . 14 $/\$
253	140	ralrimiva 2966	. . . . . . . . . . . . . 14 $/\$
254	106	elixp 7915	. . . . . . . . . . . . . 14 $/\$
255	252, 253, 254	sylanbrc 698	. . . . . . . . . . . . 13 $/\$
256		simpl 473	. . . . . . . . . . . . 13 $/\$
257	255, 256	elind 3798	. . . . . . . . . . . 12 $/\$
258		neldifsnd 4322	. . . . . . . . . . . 12 $/\$ ..^ $\$
259	257, 258	eldifd 3585	. . . . . . . . . . 11 $/\$ $\$ ..^ $\$
260	259	adantll 750	. . . . . . . . . 10 $/\$ $/\$ $\$ ..^ $\$
261		simplr 792	. . . . . . . . . . . . . . . . 17 $/\$ $/\$
262	261	anim1i 592	. . . . . . . . . . . . . . . 16 $/\$ $/\$ $/\$ ..^ $/\$ ..^
263		simpl 473	. . . . . . . . . . . . . . . 16 $/\$
264	262, 263	anim12i 590	. . . . . . . . . . . . . . 15 $/\$ $/\$ $/\$ ..^ $/\$ $/\$ $/\$ ..^ $/\$
265		elin 3796	. . . . . . . . . . . . . . . 16 $\$ ..^ $\$ $\$ $\$ ..^ $\$ $/\$ $\$
266		andir 912	. . . . . . . . . . . . . . . . 17 $/\$ $/\$ $/\$ ..^ $\/$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ $/\$ ..^ $/\$ $/\$ $\/$ $/\$ $/\$ $/\$ $/\$ $/\$
267		eldif 3584	. . . . . . . . . . . . . . . . . . 19 $\$ ..^ $\$ $/\$ ..^ $\$
268		elin 3796	. . . . . . . . . . . . . . . . . . . . 21 $/\$
269		vex 3203	. . . . . . . . . . . . . . . . . . . . . . 23
270	269	elixp 7915	. . . . . . . . . . . . . . . . . . . . . 22 $/\$
271	270	anbi1i 731	. . . . . . . . . . . . . . . . . . . . 21 $/\$ $/\$ $/\$
272	268, 271	bitri 264	. . . . . . . . . . . . . . . . . . . 20 $/\$ $/\$
273		ianor 509	. . . . . . . . . . . . . . . . . . . . 21 ..^ $/\$ ..^ $\/$
274		eldif 3584	. . . . . . . . . . . . . . . . . . . . 21 ..^ $\$ ..^ $/\$
275	273, 274	xchnxbir 323	. . . . . . . . . . . . . . . . . . . 20 ..^ $\$ ..^ $\/$
276	272, 275	anbi12i 733	. . . . . . . . . . . . . . . . . . 19 $/\$ ..^ $\$ $/\$ $/\$ $/\$ ..^ $\/$
277		andi 911	. . . . . . . . . . . . . . . . . . 19 $/\$ $/\$ $/\$ ..^ $\/$ $/\$ $/\$ $/\$ ..^ $\/$ $/\$ $/\$ $/\$
278	267, 276, 277	3bitri 286	. . . . . . . . . . . . . . . . . 18 $\$ ..^ $\$ $/\$ $/\$ $/\$ ..^ $\/$ $/\$ $/\$ $/\$
279		eldif 3584	. . . . . . . . . . . . . . . . . 18 $\$ $/\$
280	278, 279	anbi12i 733	. . . . . . . . . . . . . . . . 17 $\$ ..^ $\$ $/\$ $\$ $/\$ $/\$ $/\$ ..^ $\/$ $/\$ $/\$ $/\$ $/\$ $/\$
281		pm3.24 926	. . . . . . . . . . . . . . . . . . 19 $/\$
282		simpr 477	. . . . . . . . . . . . . . . . . . . 20 $/\$ $/\$ $/\$
283		simpr 477	. . . . . . . . . . . . . . . . . . . 20 $/\$
284	282, 283	anim12ci 591	. . . . . . . . . . . . . . . . . . 19 $/\$ $/\$ $/\$ $/\$ $/\$ $/\$
285	281, 284	mto 188	. . . . . . . . . . . . . . . . . 18 $/\$ $/\$ $/\$ $/\$ $/\$
286	285	biorfi 422	. . . . . . . . . . . . . . . . 17 $/\$ $/\$ $/\$ ..^ $/\$ $/\$ $/\$ $/\$ $/\$ ..^ $/\$ $/\$ $\/$ $/\$ $/\$ $/\$ $/\$ $/\$
287	266, 280, 286	3bitr4i 292	. . . . . . . . . . . . . . . 16 $\$ ..^ $\$ $/\$ $\$ $/\$ $/\$ $/\$ ..^ $/\$ $/\$
288	265, 287	bitri 264	. . . . . . . . . . . . . . 15 $\$ ..^ $\$ $\$ $/\$ $/\$ $/\$ ..^ $/\$ $/\$
289		ancom 466	. . . . . . . . . . . . . . . 16 ..^ $/\$ $/\$ $/\$ ..^ $/\$
290		anass 681	. . . . . . . . . . . . . . . 16 $/\$ ..^ $/\$ $/\$ ..^ $/\$
291	289, 290	bitr4i 267	. . . . . . . . . . . . . . 15 ..^ $/\$ $/\$ $/\$ ..^ $/\$
292	264, 288, 291	3imtr4i 281	. . . . . . . . . . . . . 14 $\$ ..^ $\$ $\$ ..^ $/\$ $/\$
293		ancom 466	. . . . . . . . . . . . . . . . 17 ..^ $/\$ $/\$ ..^
294		eldif 3584	. . . . . . . . . . . . . . . . 17 $\$ ..^ $/\$ ..^
295	293, 294	bitr4i 267	. . . . . . . . . . . . . . . 16 ..^ $/\$ $\$ ..^
296		imadmrn 5476	. . . . . . . . . . . . . . . . . . . . 21
297	66, 55	dmmpti 6023	. . . . . . . . . . . . . . . . . . . . . 22
298	297	imaeq2i 5464	. . . . . . . . . . . . . . . . . . . . 21
299	296, 298	eqtr3i 2646	. . . . . . . . . . . . . . . . . . . 20
300	299	difeq1i 3724	. . . . . . . . . . . . . . . . . . 19 $\$ ..^ $\$ ..^
301		imadifss 33384	. . . . . . . . . . . . . . . . . . 19 $\$ ..^ $\$ ..^
302	300, 301	eqsstri 3635	. . . . . . . . . . . . . . . . . 18 $\$ ..^ $\$ ..^
303		imass2 5501	. . . . . . . . . . . . . . . . . . . 20 $\$ ..^ $\$ ..^
304	95, 303	syl 17	. . . . . . . . . . . . . . . . . . 19 $\$ ..^
305		df-ima 5127	. . . . . . . . . . . . . . . . . . . 20
306		uznnssnn 11735	. . . . . . . . . . . . . . . . . . . . . 22
307	306	resmptd 5452	. . . . . . . . . . . . . . . . . . . . 21
308	307	rneqd 5353	. . . . . . . . . . . . . . . . . . . 20
309	305, 308	syl5eq 2668	. . . . . . . . . . . . . . . . . . 19
310	304, 309	sseqtrd 3641	. . . . . . . . . . . . . . . . . 18 $\$ ..^
311	302, 310	syl5ss 3614	. . . . . . . . . . . . . . . . 17 $\$ ..^
312	311	sseld 3602	. . . . . . . . . . . . . . . 16 $\$ ..^
313	295, 312	syl5bi 232	. . . . . . . . . . . . . . 15 ..^ $/\$
314	313	anim1d 588	. . . . . . . . . . . . . 14 ..^ $/\$ $/\$ $/\$
315	292, 314	syl5 34	. . . . . . . . . . . . 13 $\$ ..^ $\$ $\$ $/\$
316	315	eximdv 1846	. . . . . . . . . . . 12 $\$ ..^ $\$ $\$ $/\$
317		n0 3931	. . . . . . . . . . . 12 $\$ ..^ $\$ $\$ $\$ ..^ $\$ $\$
318	66	rgenw 2924	. . . . . . . . . . . . . 14
319		eqid 2622	. . . . . . . . . . . . . . 15
320		fveq1 6190	. . . . . . . . . . . . . . . . 17
321	320	eleq1d 2686	. . . . . . . . . . . . . . . 16
322	321	ralbidv 2986	. . . . . . . . . . . . . . 15
323	319, 322	rexrnmpt 6369	. . . . . . . . . . . . . 14
324	318, 323	ax-mp 5	. . . . . . . . . . . . 13
325		df-rex 2918	. . . . . . . . . . . . 13 $/\$
326	324, 325	bitr3i 266	. . . . . . . . . . . 12 $/\$
327	316, 317, 326	3imtr4g 285	. . . . . . . . . . 11 $\$ ..^ $\$ $\$
328	327	adantl 482	. . . . . . . . . 10 $/\$ $/\$ $\$ ..^ $\$ $\$
329	260, 328	embantd 59	. . . . . . . . 9 $/\$ $/\$ $\$ ..^ $\$ $\$ ..^ $\$ $\$
330	249, 329	syl5 34	. . . . . . . 8 $/\$ $/\$ $\$ ..^ $\$ ↾_t $/\$ ↾_t $\$
331	244, 330	mpand 711	. . . . . . 7 $/\$ $/\$ ↾_t $\$
332	331	ralrimdva 2969	. . . . . 6 $/\$ ↾_t $\$
333	199, 332	sylbid 230	. . . . 5 $/\$ ↾_t
334	333	reximdva 3017	. . . 4 ↾_t
335	194, 334	syld 47	. . 3
336	148, 335	pm2.61d 170	. 2
337		poimir.0	. . . 4
338		poimir.1	. . . 4 ↾_t
339		poimirlem30.x	. . . 4
340		poimirlem30.4	. . . 4 $/\$ $/\$ $/\$
341	337, 48, 149, 338, 339, 34, 39, 340	poimirlem29 33438	. . 3 ↾_t
342	341	reximdv 3016	. 2 ↾_t
343	336, 342	mpd 15	1 ↾_t

Colors of variables: wff setvar class

Syntax hints:

wn 3

wi 4

wb 196 $\/$ wo 383 $/\$ wa 384 $/\$ w3a 1037

wal 1481

wceq 1483

wtru 1484

wex 1704

wcel 1990

cab 2608

wne 2794

wral 2912

wrex 2913

crab 2916

cvv 3200 $\$ cdif 3571

cun 3572

cin 3573

wss 3574

c0 3915

csn 4177

cpr 4179

cuni 4436

ciun 4520 class class class wbr 4653

cmpt 4729

cxp 5112

ccnv 5113

cdm 5114

crn 5115

cres 5116

cima 5117

ccom 5118

wfun 5882

wfn 5883

wf 5884

wf1o 5887

cfv 5888 (class class class)co 6650

cof 6895

com 7065

c1st 7166

c2nd 7167

cmap 7857

cixp 7908

cen 7952

cfn 7955

cr 9935

cc0 9936

c1 9937

caddc 9939

cmul 9941

cxr 10073

clt 10074

cle 10075

cmin 10266

cdiv 10684

cn 11020

cn0 11292

cuz 11687

crp 11832

cioo 12175

cicc 12178

cfz 12326 ..^cfzo 12465

cabs 13974 ↾_t crest 16081

ctg 16098

cpt 16099

cxmt 19731

cbl 19733

cmopn 19736

ctop 20698

ccld 20820

clp 20938

ccn 21028

ct1 21111

cha 21112

ccmp 21189

cii 22678

This theorem was proved from axioms: ax-mp 5 ax-1 6 ax-2 7 ax-3 8 ax-gen 1722 ax-4 1737 ax-5 1839 ax-6 1888 ax-7 1935 ax-8 1992 ax-9 1999 ax-10 2019 ax-11 2034 ax-12 2047 ax-13 2246 ax-ext 2602 ax-rep 4771 ax-sep 4781 ax-nul 4789 ax-pow 4843 ax-pr 4906 ax-un 6949 ax-inf2 8538 ax-cnex 9992 ax-resscn 9993 ax-1cn 9994 ax-icn 9995 ax-addcl 9996 ax-addrcl 9997 ax-mulcl 9998 ax-mulrcl 9999 ax-mulcom 10000 ax-addass 10001 ax-mulass 10002 ax-distr 10003 ax-i2m1 10004 ax-1ne0 10005 ax-1rid 10006 ax-rnegex 10007 ax-rrecex 10008 ax-cnre 10009 ax-pre-lttri 10010 ax-pre-lttrn 10011 ax-pre-ltadd 10012 ax-pre-mulgt0 10013 ax-pre-sup 10014

This theorem depends on definitions: df-bi 197 df-or 385 df-an 386 df-3or 1038 df-3an 1039 df-tru 1486 df-ex 1705 df-nf 1710 df-sb 1881 df-eu 2474 df-mo 2475 df-clab 2609 df-cleq 2615 df-clel 2618 df-nfc 2753 df-ne 2795 df-nel 2898 df-ral 2917 df-rex 2918 df-reu 2919 df-rmo 2920 df-rab 2921 df-v 3202 df-sbc 3436 df-csb 3534 df-dif 3577 df-un 3579 df-in 3581 df-ss 3588 df-pss 3590 df-nul 3916 df-if 4087 df-pw 4160 df-sn 4178 df-pr 4180 df-tp 4182 df-op 4184 df-uni 4437 df-int 4476 df-iun 4522 df-iin 4523 df-br 4654 df-opab 4713 df-mpt 4730 df-tr 4753 df-id 5024 df-eprel 5029 df-po 5035 df-so 5036 df-fr 5073 df-we 5075 df-xp 5120 df-rel 5121 df-cnv 5122 df-co 5123 df-dm 5124 df-rn 5125 df-res 5126 df-ima 5127 df-pred 5680 df-ord 5726 df-on 5727 df-lim 5728 df-suc 5729 df-iota 5851 df-fun 5890 df-fn 5891 df-f 5892 df-f1 5893 df-fo 5894 df-f1o 5895 df-fv 5896 df-riota 6611 df-ov 6653 df-oprab 6654 df-mpt2 6655 df-of 6897 df-om 7066 df-1st 7168 df-2nd 7169 df-wrecs 7407 df-recs 7468 df-rdg 7506 df-1o 7560 df-2o 7561 df-oadd 7564 df-er 7742 df-map 7859 df-ixp 7909 df-en 7956 df-dom 7957 df-sdom 7958 df-fin 7959 df-fi 8317 df-sup 8348 df-inf 8349 df-pnf 10076 df-mnf 10077 df-xr 10078 df-ltxr 10079 df-le 10080 df-sub 10268 df-neg 10269 df-div 10685 df-nn 11021 df-2 11079 df-3 11080 df-n0 11293 df-z 11378 df-uz 11688 df-q 11789 df-rp 11833 df-xneg 11946 df-xadd 11947 df-xmul 11948 df-ioo 12179 df-icc 12182 df-fz 12327 df-fzo 12466 df-fl 12593 df-seq 12802 df-exp 12861 df-cj 13839 df-re 13840 df-im 13841 df-sqrt 13975 df-abs 13976 df-rest 16083 df-topgen 16104 df-pt 16105 df-psmet 19738 df-xmet 19739 df-met 19740 df-bl 19741 df-mopn 19742 df-top 20699 df-topon 20716 df-bases 20750 df-cld 20823 df-ntr 20824 df-cls 20825 df-lp 20940 df-cn 21031 df-cnp 21032 df-t1 21118 df-haus 21119 df-cmp 21190 df-tx 21365 df-hmeo 21558 df-hmph 21559 df-ii 22680

This theorem is referenced by: poimirlem32 33441

W3C validator