Theorem List for Metamath Proof Explorer - 20601-20700 *Has distinct variable
group(s)
| Type | Label | Description |
|---|
| Statement |
|---|
| |
| Theorem | pm2mpfval 20601* |
A polynomial matrix transformed into a polynomial over matrices.
(Contributed by AV, 4-Oct-2019.) (Revised by AV, 5-Dec-2019.)
|
    Poly1 Poly1         Mat Mat                        
 .g .g  mulGrp mulGrp         var1 var1         Mat Mat      
 Poly1 Poly1         pMatToMatPoly pMatToMatPoly             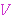   
        
   g g         decompPMat decompPMat      
      |
| |
| Theorem | pm2mpcl 20602 |
The transformation of polynomial matrices into polynomials over
matrices maps polynomial matrices to polynomials over matrices.
(Contributed by AV, 5-Oct-2019.) (Revised by AV, 5-Dec-2019.)
|
    Poly1 Poly1         Mat Mat                        
 .g .g  mulGrp mulGrp         var1 var1         Mat Mat      
 Poly1 Poly1         pMatToMatPoly pMatToMatPoly                  
               
  |
| |
| Theorem | pm2mpf 20603 |
The transformation of polynomial matrices into polynomials over
matrices is a function mapping polynomial matrices to polynomials over
matrices. (Contributed by AV, 5-Oct-2019.) (Revised by AV,
5-Dec-2019.)
|
    Poly1 Poly1         Mat Mat                        
 .g .g  mulGrp mulGrp         var1 var1         Mat Mat      
 Poly1 Poly1         pMatToMatPoly pMatToMatPoly                  
     
   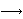   |
| |
| Theorem | pm2mpf1 20604 |
The transformation of polynomial matrices into polynomials over
matrices is a 1-1 function mapping polynomial matrices to polynomials
over matrices. (Contributed by AV, 14-Oct-2019.) (Revised by AV,
6-Dec-2019.)
|
    Poly1 Poly1         Mat Mat                        
 .g .g  mulGrp mulGrp         var1 var1         Mat Mat      
 Poly1 Poly1         pMatToMatPoly pMatToMatPoly                  
     
      |
| |
| Theorem | pm2mpcoe1 20605 |
A coefficient of the polynomial over matrices which is the result of the
transformation of a polynomial matrix is the matrix consisting of the
coefficients in the polynomial entries of the polynomial matrix.
(Contributed by AV, 20-Oct-2019.) (Revised by AV, 5-Dec-2019.)
|
    Poly1 Poly1         Mat Mat                        
 .g .g  mulGrp mulGrp         var1 var1         Mat Mat      
 Poly1 Poly1         pMatToMatPoly pMatToMatPoly          
     
             coe1 coe1         
   decompPMat decompPMat    |
| |
| Theorem | idpm2idmp 20606 |
The transformation of the identity polynomial matrix into polynomials
over matrices results in the identity of the polynomials over matrices.
(Contributed by AV, 18-Oct-2019.) (Revised by AV, 5-Dec-2019.)
|
    Poly1 Poly1         Mat Mat                        
 .g .g  mulGrp mulGrp         var1 var1         Mat Mat      
 Poly1 Poly1         pMatToMatPoly pMatToMatPoly                                |
| |
| Theorem | mptcoe1matfsupp 20607* |
The mapping extracting the entries of the coefficient matrices of a
polynomial over matrices at a fixed position is finitely supported.
(Contributed by AV, 6-Oct-2019.) (Proof shortened by AV,
23-Dec-2019.)
|
     Mat Mat        Poly1 Poly1                      
              
    
     coe1 coe1         finSupp finSupp       |
| |
| Theorem | mply1topmatcllem 20608* |
Lemma for mply1topmatcl 20610. (Contributed by AV, 6-Oct-2019.)
|
     Mat Mat        Poly1 Poly1                 Poly1 Poly1               
 .g .g  mulGrp mulGrp         var1 var1             
              
    
      coe1 coe1        
       finSupp finSupp       |
| |
| Theorem | mply1topmatval 20609* |
A polynomial over matrices transformed into a polynomial matrix.  is the inverse function of the transformation
is the inverse function of the transformation  of polynomial
matrices into polynomials over matrices: of polynomial
matrices into polynomials over matrices:             (see mp2pm2mp 20616). (Contributed by AV, 6-Oct-2019.)
(see mp2pm2mp 20616). (Contributed by AV, 6-Oct-2019.)
|
     Mat Mat        Poly1 Poly1                 Poly1 Poly1               
 .g .g  mulGrp mulGrp         var1 var1             
   
    
 g g           coe1 coe1                         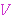                  
    
 g g           coe1 coe1                   |
| |
| Theorem | mply1topmatcl 20610* |
A polynomial over matrices transformed into a polynomial matrix is a
polynomial matrix. (Contributed by AV, 6-Oct-2019.)
|
     Mat Mat        Poly1 Poly1                 Poly1 Poly1               
 .g .g  mulGrp mulGrp         var1 var1             
   
    
 g g           coe1 coe1                         Mat Mat      
                              |
| |
| Theorem | mp2pm2mplem1 20611* |
Lemma 1 for mp2pm2mp 20616. (Contributed by AV, 9-Oct-2019.) (Revised
by
AV, 5-Dec-2019.)
|
     Mat Mat        Poly1 Poly1                        
 .g .g  mulGrp mulGrp         var1 var1             
   
    
 g g           coe1 coe1                         
               
            g g    
      coe1 coe1        
          |
| |
| Theorem | mp2pm2mplem2 20612* |
Lemma 2 for mp2pm2mp 20616. (Contributed by AV, 10-Oct-2019.)
(Revised
by AV, 5-Dec-2019.)
|
     Mat Mat        Poly1 Poly1                        
 .g .g  mulGrp mulGrp         var1 var1             
   
    
 g g           coe1 coe1                        Poly1 Poly1         Mat Mat      
                            
     g g  
        coe1 coe1        
            |
| |
| Theorem | mp2pm2mplem3 20613* |
Lemma 3 for mp2pm2mp 20616. (Contributed by AV, 10-Oct-2019.)
(Revised
by AV, 5-Dec-2019.)
|
     Mat Mat        Poly1 Poly1                        
 .g .g  mulGrp mulGrp         var1 var1             
   
    
 g g           coe1 coe1                        Poly1 Poly1             
                  decompPMat decompPMat          
    coe1 coe1    g g           coe1 coe1                       |
| |
| Theorem | mp2pm2mplem4 20614* |
Lemma 4 for mp2pm2mp 20616. (Contributed by AV, 12-Oct-2019.)
(Revised
by AV, 5-Dec-2019.)
|
     Mat Mat        Poly1 Poly1                        
 .g .g  mulGrp mulGrp         var1 var1             
   
    
 g g           coe1 coe1                        Poly1 Poly1             
                  decompPMat decompPMat      coe1 coe1       |
| |
| Theorem | mp2pm2mplem5 20615* |
Lemma 5 for mp2pm2mp 20616. (Contributed by AV, 12-Oct-2019.)
(Revised
by AV, 5-Dec-2019.)
|
     Mat Mat        Poly1 Poly1                        
 .g .g  mulGrp mulGrp         var1 var1             
   
    
 g g           coe1 coe1                        Poly1 Poly1               
 .g .g  mulGrp mulGrp         var1 var1         
                      decompPMat decompPMat           finSupp finSupp       |
| |
| Theorem | mp2pm2mp 20616* |
A polynomial over matrices transformed into a polynomial matrix
transformed back into the polynomial over matrices. (Contributed by AV,
12-Oct-2019.)
|
     Mat Mat        Poly1 Poly1                        
 .g .g  mulGrp mulGrp         var1 var1             
   
    
 g g           coe1 coe1                        Poly1 Poly1         pMatToMatPoly
pMatToMatPoly         
                      |
| |
| Theorem | pm2mpghmlem2 20617* |
Lemma 2 for pm2mpghm 20621. (Contributed by AV, 15-Oct-2019.)
(Revised
by AV, 4-Dec-2019.)
|
    Poly1 Poly1         Mat Mat                        
 .g .g  mulGrp mulGrp         var1 var1         Mat Mat      
 Poly1 Poly1                            decompPMat decompPMat      
    finSupp finSupp
      |
| |
| Theorem | pm2mpghmlem1 20618 |
Lemma 1 for pm2mpghm . (Contributed by AV, 15-Oct-2019.) (Revised by
AV, 4-Dec-2019.)
|
    Poly1 Poly1         Mat Mat                        
 .g .g  mulGrp mulGrp         var1 var1         Mat Mat      
 Poly1 Poly1                   
                  decompPMat decompPMat  
          |
| |
| Theorem | pm2mpfo 20619 |
The transformation of polynomial matrices into polynomials over
matrices is a function mapping polynomial matrices onto polynomials
over matrices. (Contributed by AV, 12-Oct-2019.) (Revised by AV,
6-Dec-2019.)
|
    Poly1 Poly1         Mat Mat                        
 .g .g  mulGrp mulGrp         var1 var1         Mat Mat      
 Poly1 Poly1                  pMatToMatPoly pMatToMatPoly                      |
| |
| Theorem | pm2mpf1o 20620 |
The transformation of polynomial matrices into polynomials over matrices
is a 1-1 function mapping polynomial matrices onto polynomials over
matrices. (Contributed by AV, 14-Oct-2019.)
|
    Poly1 Poly1         Mat Mat                        
 .g .g  mulGrp mulGrp         var1 var1         Mat Mat      
 Poly1 Poly1                  pMatToMatPoly pMatToMatPoly                      |
| |
| Theorem | pm2mpghm 20621 |
The transformation of polynomial matrices into polynomials over matrices
is an additive group homomorphism. (Contributed by AV, 16-Oct-2019.)
(Revised by AV, 6-Dec-2019.)
|
    Poly1 Poly1         Mat Mat                        
 .g .g  mulGrp mulGrp         var1 var1         Mat Mat      
 Poly1 Poly1                  pMatToMatPoly pMatToMatPoly                        |
| |
| Theorem | pm2mpgrpiso 20622 |
The transformation of polynomial matrices into polynomials over matrices
is an additive group isomorphism. (Contributed by AV, 17-Oct-2019.)
|
    Poly1 Poly1         Mat Mat                        
 .g .g  mulGrp mulGrp         var1 var1         Mat Mat      
 Poly1 Poly1                  pMatToMatPoly pMatToMatPoly                    GrpIso GrpIso    |
| |
| Theorem | pm2mpmhmlem1 20623* |
Lemma 1 for pm2mpmhm 20625. (Contributed by AV, 21-Oct-2019.)
(Revised by
AV, 6-Dec-2019.)
|
    Poly1 Poly1         Mat Mat                        
 .g .g  mulGrp mulGrp         var1 var1         Mat Mat      
 Poly1 Poly1                  pMatToMatPoly pMatToMatPoly          
     
            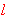
       g g       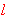      decompPMat decompPMat
         decompPMat decompPMat  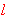          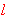
     finSupp finSupp       |
| |
| Theorem | pm2mpmhmlem2 20624* |
Lemma 2 for pm2mpmhm 20625. (Contributed by AV, 22-Oct-2019.)
(Revised
by AV, 6-Dec-2019.)
|
    Poly1 Poly1         Mat Mat         Mat Mat        Poly1 Poly1         pMatToMatPoly
pMatToMatPoly                                                                 |
| |
| Theorem | pm2mpmhm 20625 |
The transformation of polynomial matrices into polynomials over matrices
is a homomorphism of multiplicative monoids. (Contributed by AV,
22-Oct-2019.) (Revised by AV, 6-Dec-2019.)
|
    Poly1 Poly1         Mat Mat         Mat Mat        Poly1 Poly1         pMatToMatPoly
pMatToMatPoly         
     
    mulGrp mulGrp   MndHom MndHom  mulGrp mulGrp     |
| |
| Theorem | pm2mprhm 20626 |
The transformation of polynomial matrices into polynomials over matrices
is a ring homomorphism. (Contributed by AV, 22-Oct-2019.)
|
    Poly1 Poly1         Mat Mat         Mat Mat        Poly1 Poly1         pMatToMatPoly
pMatToMatPoly         
     
    RingHom
RingHom    |
| |
| Theorem | pm2mprngiso 20627 |
The transformation of polynomial matrices into polynomials over matrices
is a ring isomorphism. (Contributed by AV, 22-Oct-2019.)
|
    Poly1 Poly1         Mat Mat         Mat Mat        Poly1 Poly1         pMatToMatPoly
pMatToMatPoly         
     
    RingIso
RingIso    |
| |
| Theorem | pmmpric 20628 |
The ring of polynomial matrices over a ring is isomorphic to the ring of
polynomials over matrices of the same dimension over the same ring.
(Contributed by AV, 30-Dec-2019.)
|
    Poly1 Poly1         Mat Mat         Mat Mat        Poly1 Poly1         
     
 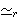   |
| |
| Theorem | monmat2matmon 20629 |
The transformation of a polynomial matrix having scaled monomials with
the same power as entries into a scaled monomial as a polynomial over
matrices. (Contributed by AV, 11-Nov-2019.) (Revised by AV,
7-Dec-2019.)
|
    Poly1 Poly1         Mat Mat                        
 .g .g  mulGrp mulGrp         var1 var1         Mat Mat      
          Poly1 Poly1         pMatToMatPoly pMatToMatPoly        .g .g  mulGrp mulGrp         var1 var1      
           matToPolyMat matToPolyMat          
     
                                       |
| |
| Theorem | pm2mp 20630* |
The transformation of a sum of matrices having scaled monomials with the
same power as entries into a sum of scaled monomials as a polynomial
over matrices. (Contributed by AV, 12-Nov-2019.) (Revised by AV,
7-Dec-2019.)
|
    Poly1 Poly1         Mat Mat                        
 .g .g  mulGrp mulGrp         var1 var1         Mat Mat      
          Poly1 Poly1         pMatToMatPoly pMatToMatPoly        .g .g  mulGrp mulGrp         var1 var1      
           matToPolyMat matToPolyMat          
     
          finSupp finSupp
              g g                              g g           
          |
| |
| 11.5 The characteristic
polynomial
According to Wikipedia ("Characteristic polynomial", 31-Jul-2019,
https://en.wikipedia.org/wiki/Characteristic_polynomial):
"In linear
algebra, the characteristic polynomial of a square matrix is a polynomial
which is invariant under matrix similarity and has the eigenvalues as roots.
It has the determinant and the trace of the matrix as coefficients.".
Based
on the definition of the characteristic polynomial of a square matrix
(df-chpmat 20632) the eigenvalues and corresponding
eigenvectors can be
defined.
|
| |
| 11.5.1 Definition and basic
properties
The characteristic polynomial of a matrix  is the determinat of the
characteristic matrix of is the determinat of the
characteristic matrix of  : :       . .
|
| |
| Syntax | cchpmat 20631 |
Extend class notation with the characteristic polynomial.
|
 CharPlyMat CharPlyMat |
| |
| Definition | df-chpmat 20632* |
Define the characteristic polynomial of a square matrix. According to
Wikipedia ("Characteristic polynomial", 31-Jul-2019,
https://en.wikipedia.org/wiki/Characteristic_polynomial):
"The
characteristic polynomial of [an n x n matrix] A, denoted by pA(t), is
the polynomial defined by pA ( t ) =
det ( t I - A ) where I denotes
the n-by-n identity matrix.". In addition, however, the underlying
ring
must be commutative, see definition in [Lang], p. 561: " Let k be a
commutative ring ... Let M be any n x n matrix in k ... We define the
characteristic polynomial PM(t) to be
the determinant det ( t In - M )
where In is the unit n x n
matrix." To be more precise, the matrices A
and I on the right hand side are matrices with coefficients of a
polynomial ring. Therefore, the original matrix A over a given
commutative ring must be transformed into corresponding matrices over
the polynomial ring over the given ring. (Contributed by AV,
2-Aug-2019.)
|
 CharPlyMat CharPlyMat                   Mat Mat        maDet maDet  Poly1 Poly1        var1 var1        Mat Mat  Poly1 Poly1          Mat Mat  Poly1 Poly1           Mat Mat  Poly1 Poly1        matToPolyMat
matToPolyMat          |
| |
| Theorem | chmatcl 20633 |
Closure of the characteristic matrix of a matrix. (Contributed by AV,
25-Oct-2019.) (Proof shortened by AV, 29-Nov-2019.)
|
     Mat Mat                 Poly1 Poly1         Mat Mat      
 var1 var1         matToPolyMat matToPolyMat     
                                               
                  |
| |
| Theorem | chmatval 20634 |
The entries of the characteristic matrix of a matrix. (Contributed by
AV, 2-Aug-2019.) (Proof shortened by AV, 10-Dec-2019.)
|
     Mat Mat                 Poly1 Poly1         Mat Mat      
 var1 var1         matToPolyMat matToPolyMat     
                                                     
            
                                                              |
| |
| Theorem | chpmatfval 20635* |
Value of the characteristic polynomial function. (Contributed by AV,
2-Aug-2019.)
|
     CharPlyMat CharPlyMat         Mat Mat                 Poly1 Poly1         Mat Mat      
  maDet maDet     
           var1 var1               
  matToPolyMat matToPolyMat      
               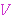                 
           |
| |
| Theorem | chpmatval 20636 |
The characteristic polynomial of a (square) matrix (expressed with a
determinant). (Contributed by AV, 2-Aug-2019.)
|
     CharPlyMat CharPlyMat         Mat Mat                 Poly1 Poly1         Mat Mat      
  maDet maDet     
           var1 var1               
  matToPolyMat matToPolyMat      
               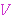   
        
         
        |
| |
| Theorem | chpmatply1 20637 |
The characteristic polynomial of a (square) matrix over a commutative
ring is a polynomial, see also the following remark in [Lang], p. 561:
"[the characteristic polynomial] is an element of k[t]".
(Contributed by AV, 2-Aug-2019.) (Proof shortened by AV,
29-Nov-2019.)
|
     CharPlyMat CharPlyMat         Mat Mat                 Poly1 Poly1                                     |
| |
| Theorem | chpmatval2 20638* |
The characteristic polynomial of a (square) matrix (expressed with the
Leibnitz formula for the determinant). (Contributed by AV,
2-Aug-2019.)
|
     CharPlyMat CharPlyMat         Mat Mat                 Poly1 Poly1         Mat Mat                 var1 var1      
           matToPolyMat matToPolyMat               
 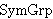                   RHom RHom        pmSgn pmSgn        mulGrp mulGrp     
            
               
   g g   
      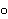        
 g g               
                 |
| |
| Theorem | chpmat0d 20639 |
The characteristic polynomial of the empty matrix. (Contributed by AV,
6-Aug-2019.)
|
     CharPlyMat CharPlyMat                    Poly1 Poly1     |
| |
| Theorem | chpmat1dlem 20640 |
Lemma for chpmat1d 20641. (Contributed by AV, 7-Aug-2019.)
|
     CharPlyMat CharPlyMat        Poly1 Poly1         Mat Mat                 var1 var1               
 algSc algSc         Mat Mat         matToPolyMat matToPolyMat                
   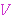                                                    |
| |
| Theorem | chpmat1d 20641 |
The characteristic polynomial of a matrix with dimension 1.
(Contributed by AV, 7-Aug-2019.)
|
     CharPlyMat CharPlyMat        Poly1 Poly1         Mat Mat                 var1 var1               
 algSc algSc                
   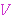                            |
| |
| Theorem | chpdmatlem0 20642 |
Lemma 0 for chpdmat 20646. (Contributed by AV, 18-Aug-2019.)
|
     CharPlyMat CharPlyMat        Poly1 Poly1         Mat Mat        algSc algSc                 var1 var1                 mulGrp mulGrp      
           Mat Mat               
                       
      |
| |
| Theorem | chpdmatlem1 20643 |
Lemma 1 for chpdmat 20646. (Contributed by AV, 18-Aug-2019.)
|
     CharPlyMat CharPlyMat        Poly1 Poly1         Mat Mat        algSc algSc                 var1 var1                 mulGrp mulGrp      
           Mat Mat               
                    matToPolyMat
matToPolyMat         
                              |
| |
| Theorem | chpdmatlem2 20644 |
Lemma 2 for chpdmat 20646. (Contributed by AV, 18-Aug-2019.)
|
     CharPlyMat CharPlyMat        Poly1 Poly1         Mat Mat        algSc algSc                 var1 var1                 mulGrp mulGrp      
           Mat Mat               
                    matToPolyMat
matToPolyMat             
                        
               
                 |
| |
| Theorem | chpdmatlem3 20645 |
Lemma 3 for chpdmat 20646. (Contributed by AV, 18-Aug-2019.)
|
     CharPlyMat CharPlyMat        Poly1 Poly1         Mat Mat        algSc algSc                 var1 var1                 mulGrp mulGrp      
           Mat Mat               
                    matToPolyMat
matToPolyMat             
                  
                         |
| |
| Theorem | chpdmat 20646* |
The characteristic polynomial of a diagonal matrix. (Contributed by AV,
18-Aug-2019.) (Proof shortened by AV, 21-Nov-2019.)
|
     CharPlyMat CharPlyMat        Poly1 Poly1         Mat Mat        algSc algSc                 var1 var1                 mulGrp mulGrp      
            
                                
         g g       
              |
| |
| Theorem | chpscmat 20647* |
The characteristic polynomial of a (nonempty!) scalar matrix.
(Contributed by AV, 21-Aug-2019.)
|
     CharPlyMat CharPlyMat        Poly1 Poly1         Mat Mat        var1 var1        mulGrp mulGrp        .g .g         
        
                     
                 algSc algSc     
                
    
   
                      
        
         |
| |
| Theorem | chpscmat0 20648* |
The characteristic polynomial of a (nonempty!) scalar matrix,
expressed with its diagonal element. (Contributed by AV,
21-Aug-2019.)
|
     CharPlyMat CharPlyMat        Poly1 Poly1         Mat Mat        var1 var1        mulGrp mulGrp        .g .g         
        
                     
                 algSc algSc     
                
    
   
                          
        
             |
| |
| Theorem | chpscmatgsumbin 20649* |
The characteristic polynomial of a (nonempty!) scalar matrix,
expressed as finite group sum of binomials. (Contributed by AV,
2-Sep-2019.)
|
     CharPlyMat CharPlyMat        Poly1 Poly1         Mat Mat        var1 var1        mulGrp mulGrp        .g .g         
        
                     
                 algSc algSc     
           .g .g        mulGrp mulGrp        .g .g               
                
    
                              
   g g  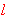          
        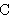 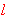            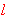             
 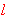         |
| |
| Theorem | chpscmatgsummon 20650* |
The characteristic polynomial of a (nonempty!) scalar matrix,
expressed as finite group sum of scaled monomials. (Contributed by
AV, 2-Sep-2019.)
|
     CharPlyMat CharPlyMat        Poly1 Poly1         Mat Mat        var1 var1        mulGrp mulGrp        .g .g         
        
                     
                 algSc algSc     
           .g .g        mulGrp mulGrp        .g .g               
           .g .g             
    
                              
   g g  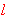          
         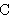 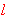           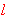              
 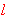        |
| |
| Theorem | chp0mat 20651 |
The characteristic polynomial of the zero matrix. (Contributed by AV,
18-Aug-2019.)
|
     CharPlyMat CharPlyMat        Poly1 Poly1         Mat Mat        var1 var1        mulGrp mulGrp        .g .g                                         |
| |
| Theorem | chpidmat 20652 |
The characteristic polynomial of the identity matrix. (Contributed by
AV, 19-Aug-2019.)
|
     CharPlyMat CharPlyMat        Poly1 Poly1         Mat Mat        var1 var1        mulGrp mulGrp        .g .g               
 algSc algSc      
       
            
     
                        |
| |
| Theorem | chmaidscmat 20653 |
The characteristic polynomial of a matrix multiplied with the identity
matrix is a scalar matrix. (Contributed by AV, 30-Oct-2019.) (Revised
by AV, 19-Dec-2019.)
|
     Mat Mat                  CharPlyMat CharPlyMat
       Poly1 Poly1                  Mat Mat      
       
                  
           ScMat ScMat         
               
      |
| |
| 11.5.2 The characteristic factor function
G
In this subsection the function      
                
                                                                 
               is discussed.
This function is involved in the representation of the product of the
characteristic matrix of a given matrix and its adjunct as an infinite sum,
see cpmadugsum 20683. Therefore, this function is called
"characteristic factor
function" (in short "chfacf") in the following. It plays an
important role in
the proof of the Cayley-Hamilton theorem, see cayhamlem1 20671, cayhamlem3 20692 and
cayhamlem4 20693. is discussed.
This function is involved in the representation of the product of the
characteristic matrix of a given matrix and its adjunct as an infinite sum,
see cpmadugsum 20683. Therefore, this function is called
"characteristic factor
function" (in short "chfacf") in the following. It plays an
important role in
the proof of the Cayley-Hamilton theorem, see cayhamlem1 20671, cayhamlem3 20692 and
cayhamlem4 20693.
|
| |
| Theorem | fvmptnn04if 20654* |
The function values of a mapping from the nonnegative integers with
four distinct cases. (Contributed by AV, 10-Nov-2019.)
|
      
    
   
   
   
                                      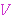                   ![]_ ]_](_urbrack.gif)                 
      ![]_ ]_](_urbrack.gif)                    ![]_ ]_](_urbrack.gif)                    ![]_ ]_](_urbrack.gif)                |
| |
| Theorem | fvmptnn04ifa 20655* |
The function value of a mapping from the nonnegative integers with four
distinct cases for the first case. (Contributed by AV, 10-Nov-2019.)
|
      
    
   
   
   
                                       
     ![]_ ]_](_urbrack.gif)   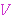 
           ![]_ ]_](_urbrack.gif)   |
| |
| Theorem | fvmptnn04ifb 20656* |
The function value of a mapping from the nonnegative integers with four
distinct cases for the second case. (Contributed by AV,
10-Nov-2019.)
|
      
    
   
   
   
                                       
           ![]_ ]_](_urbrack.gif)  
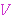        
    ![]_ ]_](_urbrack.gif)   |
| |
| Theorem | fvmptnn04ifc 20657* |
The function value of a mapping from the nonnegative integers with four
distinct cases for the third case. (Contributed by AV, 10-Nov-2019.)
|
      
    
   
   
   
                                       
     ![]_ ]_](_urbrack.gif)   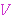 
           ![]_ ]_](_urbrack.gif)   |
| |
| Theorem | fvmptnn04ifd 20658* |
The function value of a mapping from the nonnegative integers with four
distinct cases for the forth case. (Contributed by AV, 10-Nov-2019.)
|
      
    
   
   
   
                                             ![]_ ]_](_urbrack.gif)   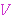 
           ![]_ ]_](_urbrack.gif)   |
| |
| Theorem | chfacfisf 20659* |
The "characteristic factor function" is a function from the
nonnegative
integers to polynomial matrices. (Contributed by AV, 8-Nov-2019.)
|
     Mat Mat                 Poly1 Poly1         Mat Mat              
                     matToPolyMat matToPolyMat               
    
                     
                       
             
           
                       
              
   
                    |
| |
| Theorem | chfacfisfcpmat 20660* |
The "characteristic factor function" is a function from the
nonnegative integers to constant polynomial matrices. (Contributed by
AV, 19-Nov-2019.)
|
     Mat Mat                 Poly1 Poly1         Mat Mat              
                     matToPolyMat matToPolyMat               
    
                     
                       
             
           
                      ConstPolyMat ConstPolyMat          
              
   
                |
| |
| Theorem | chfacffsupp 20661* |
The "characteristic factor function" is finitely supported.
(Contributed by AV, 20-Nov-2019.) (Proof shortened by AV,
23-Dec-2019.)
|
     Mat Mat                 Poly1 Poly1         Mat Mat              
                     matToPolyMat matToPolyMat               
    
                     
                       
             
           
                       
              
   
           finSupp finSupp       |
| |
| Theorem | chfacfscmulcl 20662* |
Closure of a scaled value of the "characteristic factor function".
(Contributed by AV, 9-Nov-2019.)
|
     Mat Mat                 Poly1 Poly1         Mat Mat              
                     matToPolyMat matToPolyMat               
    
                     
                       
             
           
                     var1 var1     
           .g .g  mulGrp mulGrp           
              
   
             
                    |
| |
| Theorem | chfacfscmul0 20663* |
A scaled value of the "characteristic factor function" is zero almost
always. (Contributed by AV, 9-Nov-2019.)
|
     Mat Mat                 Poly1 Poly1         Mat Mat              
                     matToPolyMat matToPolyMat               
    
                     
                       
             
           
                     var1 var1     
           .g .g  mulGrp mulGrp           
              
   
            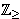         
                |
| |
| Theorem | chfacfscmulfsupp 20664* |
A mapping of scaled values of the "characteristic factor function" is
finitely supported. (Contributed by AV, 8-Nov-2019.)
|
     Mat Mat                 Poly1 Poly1         Mat Mat              
                     matToPolyMat matToPolyMat               
    
                     
                       
             
           
                     var1 var1     
           .g .g  mulGrp mulGrp           
              
   
                  
          finSupp finSupp   |
| |
| Theorem | chfacfscmulgsum 20665* |
Breaking up a sum of values of the "characteristic factor function"
scaled by a polynomial. (Contributed by AV, 9-Nov-2019.)
|
     Mat Mat                 Poly1 Poly1         Mat Mat              
                     matToPolyMat matToPolyMat               
    
                     
                       
             
           
                     var1 var1     
           .g .g  mulGrp mulGrp         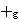           
              
   
             g g           
              g g                         
           
                        
                                  |
| |
| Theorem | chfacfpmmulcl 20666* |
Closure of the value of the "characteristic factor function"
multiplied
with a constant polynomial matrix. (Contributed by AV, 23-Nov-2019.)
|
     Mat Mat                 Poly1 Poly1         Mat Mat              
                     matToPolyMat matToPolyMat               
    
                     
                       
             
           
                  
  .g .g  mulGrp mulGrp           
              
   
             
                        |
| |
| Theorem | chfacfpmmul0 20667* |
The value of the "characteristic factor function" multiplied with a
constant polynomial matrix is zero almost always. (Contributed by AV,
23-Nov-2019.)
|
     Mat Mat                 Poly1 Poly1         Mat Mat              
                     matToPolyMat matToPolyMat               
    
                     
                       
             
           
                  
  .g .g  mulGrp mulGrp           
              
   
            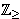         
                    |
| |
| Theorem | chfacfpmmulfsupp 20668* |
A mapping of values of the "characteristic factor function"
multiplied
with a constant polynomial matrix is finitely supported. (Contributed
by AV, 23-Nov-2019.)
|
     Mat Mat                 Poly1 Poly1         Mat Mat              
                     matToPolyMat matToPolyMat               
    
                     
                       
             
           
                  
  .g .g  mulGrp mulGrp           
              
   
                  
              finSupp finSupp   |
| |
| Theorem | chfacfpmmulgsum 20669* |
Breaking up a sum of values of the "characteristic factor function"
multiplied with a constant polynomial matrix. (Contributed by AV,
23-Nov-2019.)
|
     Mat Mat                 Poly1 Poly1         Mat Mat              
                     matToPolyMat matToPolyMat               
    
                     
                       
             
           
                  
  .g .g  mulGrp mulGrp         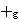           
              
   
             g g                
             g g                             
           
                        
                 
                    |
| |
| Theorem | chfacfpmmulgsum2 20670* |
Breaking up a sum of values of the "characteristic factor function"
multiplied with a constant polynomial matrix. (Contributed by AV,
23-Nov-2019.)
|
     Mat Mat                 Poly1 Poly1         Mat Mat              
                     matToPolyMat matToPolyMat               
    
                     
                       
             
           
                  
  .g .g  mulGrp mulGrp         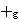           
              
   
             g g                
             g g                     
                             
                             
                
              |
| |
| Theorem | cayhamlem1 20671* |
Lemma 1 for cayleyhamilton 20695. (Contributed by AV, 11-Nov-2019.)
|
     Mat Mat                 Poly1 Poly1         Mat Mat              
                     matToPolyMat matToPolyMat               
    
                     
                       
             
           
                  
  .g .g  mulGrp mulGrp           
              
   
             g g                
           |
| |
| 11.5.3 The Cayley-Hamilton theorem
In this section, a direct algebraic proof for the Cayley-Hamilton theorem is
provided, according to Wikipedia ("Cayley-Hamilton theorem", 09-Nov-2019,
https://en.wikipedia.org/wiki/Cayley%E2%80%93Hamilton_theorem, section
"A direct algebraic proof" (this approach is also used for proving Lemma 1.9 in
[Hefferon] p. 427):
"This proof uses just the kind of objects needed to formulate the
Cayley-Hamilton theorem: matrices with polynomials as entries. The matrix
(t * In - A) whose determinant is the characteristic polynomial of A is such a
matrix, and since polynomials [over a commutative ring] form a commutative
ring, it has an adjugate
(1) B = adj(t * In - A) .
Then, according to the right-hand fundamental relation of the adjugate, one has
(2) ( t * In - A ) x B = det(t * In - A) x In = p(t) * In .
Since B is also a matrix with polynomials in t as entries, one can, for each i,
collect the coefficients of t^i in each entry to form a matrix Bi of numbers,
such that one has
(3) B = sumi = 0 to (n-1) t^i Bi .
(The way the entries of B are defined makes clear that no powers higher than
t^(n-1) occur). While this looks like a polynomial with matrices as
coefficients, we shall not consider such a notion; it is just a way to write a
matrix with polynomial entries as a linear combination of n constant matrices,
and the coefficient t^i has been written to the left of the matrix to stress
this point of view.
Now, one can expand the matrix product in our equation by bilinearity
(4) p(t) * In = ( t * In - A ) x B
= ( t * In - A ) x sumi = 0 to (n-1) t^i * Bi
= sumi = 0 to (n-1) t * In x t^i Bi
- sumi = 0 to (n-1) A * t^i Bi
= sumi = 0 to (n-1) t^(i+1) * Bi
- sumi = 0 to (n-1) t^i * A x Bi
= t^n Bn-1
+ sumi = 1 to (n-1) t^i * ( Bi-1 - A x Bi )
- A x B0 .
Writing
(5) p(t) In = t^n * In + t^(n-1) * c(n-1) x In + ...
+ t * c1 In + c0 In ,
one obtains an equality of two matrices with polynomial entries, written as
linear combinations of constant matrices with powers of t as coefficients.
Such an equality can hold only if in any matrix position the entry that is
multiplied by a given power t^i is the same on both sides; it follows that the
constant matrices with coefficient t^i in both expressions must be equal.
Writing these equations then for i from n down to 0, one finds
(6) Bn-1 = In ,
Bi-1 - A x Bi = ci * In for 1 <= i <= n-1 ,
- A x B0 = c0 * In .
Finally, multiply the equation of the coefficients of t^i from the left by A^i,
and sum up:
(7) A^n Bn-1 + sumi
= 1 to (n-1) ( A^i x Bi-1 - A^(i+1) x Bi )
- A x B0 = A^n + cn-1 * A^(n-1) + ... + c1 * A + c0 * In .
The left-hand sides form a telescoping sum and cancel completely; the
right-hand sides add up to p(A):
(8) 0 = p(A) .
This completes the proof."
To formalize this approach, the steps mentioned in Wikipedia must be elaborated
in more detail.
The first step is to formalize the preliminaries and the objective of the
theorem. In Wikipedia, the Cayley-Hamilton theorem is stated as follows:
"... the Cayley-Hamilton theorem ... states that every square matrix over a
commutative ring ... satisfies its own characteristic equation." Or in more
detail: "If A is a given n x n matrix and In is the n x n identity matrix,
then the characteristic polynomial of A is defined as p(t) = det(t * In - A),
where det is the determinant operation and t is a variable for a scalar element
of the base ring. Since the entries of the matrix (t * In - A) are (linear or
constant) polynomials in t, the determinant is also an n-th order monic
polynomial in t. The Cayley-Hamilton theorem states that if one defines an
analogous matrix equation, p(A), consisting of the replacement of the scalar
eigenvalues t with the matrix A, then this polynomial in the matrix A results
in the zero matrix,
p(A) = 0.
The powers of A, obtained by substitution from powers of t, are defined by
repeated matrix multiplication; the constant term of p(t) gives a multiple of
the power A^0, which is defined as the identity matrix. The theorem allows A^n
to be expressed as a linear combination of the lower matrix powers of A. When
the ring is a field, the Cayley-Hamilton theorem is equivalent to the statement
that the minimal polynomial of a square matrix divides its characteristic
polynomial."
Actually, the definition of the characteristic polynomial of a square matrix
requires some attention. According to df-chpmat 20632, the characteristic
polynomial of an  x x  matrix matrix  over a ring over a ring  is defined as is defined as
   CharPlyMat CharPlyMat                        
where     maDet maDet   is the function mapping an is the function mapping an  x x  matrix
over the polynomial ring over the ring matrix
over the polynomial ring over the ring  to its determinant, to its determinant,
   var1 var1   is the variable of the polynomials over is the variable of the polynomials over  , ,  is the
is the  x x  identity matrix as matrix over the polynomial ring over
the ring identity matrix as matrix over the polynomial ring over
the ring  (not the (not the  x x  identity matrix of the matrices over the
ring identity matrix of the matrices over the
ring  !) and !) and          matToPolyMat matToPolyMat      is the matrix is the matrix
 over a ring over a ring  transformed into a constant matrix over the polynomial
ring over the ring transformed into a constant matrix over the polynomial
ring over the ring  . Thus . Thus  is the multiplication of a polynomial
matrix with a "scalar", i.e. a polynomial (see chpmatval 20636). is the multiplication of a polynomial
matrix with a "scalar", i.e. a polynomial (see chpmatval 20636).
By this definition, it is ensured that              ,
the matrix whose determinat is the characteristic polynomial of the matrix ,
the matrix whose determinat is the characteristic polynomial of the matrix
 , is actually a matrix over the polynomial ring over the ring , is actually a matrix over the polynomial ring over the ring  ,
as stated in Wikipedia ("matrix with polynomials as entries"). This matrix is
called the characteristic matrix of matrix ,
as stated in Wikipedia ("matrix with polynomials as entries"). This matrix is
called the characteristic matrix of matrix  (see Wikipedia "Polynomial
matrix", 16-Nov-2019, https://en.wikipedia.org/wiki/Polynomial_matrix).
Following the notation in Wikipedia, we denote the characteristic polynomial of
the matrix (see Wikipedia "Polynomial
matrix", 16-Nov-2019, https://en.wikipedia.org/wiki/Polynomial_matrix).
Following the notation in Wikipedia, we denote the characteristic polynomial of
the matrix  , formally defined by , formally defined by    CharPlyMat CharPlyMat      as
"p(M)" in the comments. The characteristric matrix as
"p(M)" in the comments. The characteristric matrix              will be denoted by "c(M)", so that "p(M) = det( c(M) )". will be denoted by "c(M)", so that "p(M) = det( c(M) )".
After the preliminaries are clarified, the objective of the Cayley-Hamilton
theorem must be considered. As described in Wikipedia, the matrix  must be
"inserted" into its characteristic polynomial in an appropriate way. Since
every polynomial can be represented as infinite, but finitely supported sum
of monomials scaled by the corresponding coefficients (see ply1coe 19666), also
the characteristic polynomial can be written in this way: must be
"inserted" into its characteristic polynomial in an appropriate way. Since
every polynomial can be represented as infinite, but finitely supported sum
of monomials scaled by the corresponding coefficients (see ply1coe 19666), also
the characteristic polynomial can be written in this way:
p(M) = sumi ( pi * M^i )
Here, * is the scalar multiplication in the algebra of the polynomials over the
ring  , and the coefficients are elements of the ring , and the coefficients are elements of the ring  . .
By this, we can "define" the insertion of the matrix M into its characteristic
polynomial by "p(M) = sum( pi * M^i)", see also cayleyhamilton1 20697.
Here, * is the scalar multiplication in the algebra of the matrices over the
ring  . .
To prove the Cayley-Hamilton theorem, we have to show that "p(M) = 0", where 0
is the zero matrix.
In this section, the following class variables and informal identifiers
(acronyms in the form "A(B)" or "AB") are used:
| class variable/ informal identifier |
definiens |
explanation |
 |
|
An arbitrary finite set, used as dimension for matrices |
 |
|
An arbitrary (commutative) ring:    |
| B(R) |
     |
Base set of (the ring)  |
 |
  Mat Mat   |
Algebra of  x x  matrices over (the ring) matrices over (the ring)  |
 |
     |
Base set of the algebra of  x x  matrices, i .e. the set of all matrices, i .e. the set of all
 x x  matrices matrices |
 |
|
An arbitrary  x x  matrix matrix |
 |
 Poly1 Poly1   |
The algebra of polynomials over (the ring)  |
| B(P) |
     |
Base set of the algebra of polynomials, i .e. the set of all
polynomials |
 , XR , XR |
 var1 var1   |
The variable of polynomials over (the ring)  |
 , XA , XA |
 var1 var1   |
The variable of polynomials over matrices of the algebra  |
 |
 .g .g  mulGrp mulGrp    |
The group exponentiation for polynomials over (the ring)  |
| ^ |
|
Arbitrary group exponentiation |
 |
 algSc algSc   |
The injection of scalars, i.e. elements of (the ring)  into the
base set of the algebra of polynomials over into the
base set of the algebra of polynomials over  |
     , S(p) , S(p) |
  algSc algSc      |
The element  of (the ring) of (the ring)  represented as polynomial over represented as polynomial over
 |
 |
  Mat Mat   |
Algebra of  x x  matrices over (the polynomial ring) matrices over (the polynomial ring)  over the ring
over the ring  |
| B(Y) |
     |
Base set of the algebra of polynomial  x x  matrices, i .e. the
set of all polynomial matrices, i .e. the
set of all polynomial  x x  matrices matrices |
 |
 Poly1 Poly1   |
Algebra of polynomials over the ring of  x x  matrices over
the ring matrices over
the ring  |
| B(Q) |
     |
Base set of the algebra of polynomials over the ring of  x x  matrices over the ring
matrices over the ring  , i .e. the set of all polynomials having , i .e. the set of all polynomials having
 x x  matrices as coefficients matrices as coefficients |
 , + , + |
 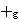    |
The addition of polynomial matrices |
 , - , - |
     |
The subtraction of polynomial matrices |
 , *Y , *Y |
     |
The multiplication of a polynomial matrix with a scalar
( i. e. a polynomial) |
| *A |
     |
The multiplication of a matrix with a scalar ( i. e. an element of the
underlying ring) |
| *Q |
     |
The multiplication of a polynomial over matrices with a scalar ( i. e.
a matrix) |
 , xY , xY |
     |
The multiplication of polynomial matrices |
| xA |
     |
The multiplication of matrices |
| xQ |
     |
The multiplication of polynomials over matrices |
 , 1Y , 1Y |
     |
The identity matrix in the algebra of polynomial matrices over 
|
| 1A |
     |
The identity matrix in the algebra of matrices over  |
 , 0Y , 0Y |
     |
The zero matrix in the algebra of matrices consisting of
polynomials |
 |
  matToPolyMat matToPolyMat   |
The transformation of an  x x  matrix over matrix over  into a
polynomial into a
polynomial  x x  matrix over matrix over  |
| T1(M) |
     |
The matrix M transformed into a polynomial  x x  matrix over matrix over
 |
| U(M) |
     |
The (constant) polynomial  x x  matrix M transformed into a
matrix over the ring matrix M transformed into a
matrix over the ring  . Inverse function of . Inverse function of  : :
           (see m2cpminvid2 20560 ) (see m2cpminvid2 20560 ) |
| T2(M) |
   pMatToMatPoly pMatToMatPoly      |
The polynomial  x x  matrix M transformed into a polynomial
over the matrix M transformed into a polynomial
over the  x x  matrices over matrices over  |
 , c(M) , c(M) |
             |
The characteristic matrix of a matrix  , i.e. the matrix whose
determinant is the characteristic polynomial of the matrix , i.e. the matrix whose
determinant is the characteristic polynomial of the matrix  |
 |
  CharPlyMat CharPlyMat   |
The function mapping a matrix over (a ring)  to its
characteristic polynomial to its
characteristic polynomial |
 , p(M) , p(M) |
     |
The characteristic polynomial of a matrix over (a ring)  |
 |
     |
The scalar matrix (diagonal matrix) with the characteristic polynomial
of a matrix as diagional elements |
 |
  maAdju maAdju   |
The function mapping a matrix consisting of polynomials to its
adjugate ("matrix of cofactors") |
 , adj(cm(M)) , adj(cm(M)) |
     |
The adjugate of the characteristic matrix of the matrix  |
Using this notation, we have:
- "c(M) e. B(Y)", or
       , see chmatcl 20633 , see chmatcl 20633
- "p(M) e. B(P)", or
       , see chpmatply1 20637 , see chpmatply1 20637
- "T(M) e. B(Y)", or
           ,
see mat2pmatbas 20531 ,
see mat2pmatbas 20531
-
       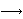      , see maduf 20447 , see maduf 20447
- "adj(cm(M)) e. B(Y)", or
      
Following the proof shown in Wikipedia, the following steps are performed:
- Write
 , the adjugate of the characteristic matrix, as a finite sum
of scaled monomials, see pmatcollpw3fi1 20593: , the adjugate of the characteristic matrix, as a finite sum
of scaled monomials, see pmatcollpw3fi1 20593:
adj(cm(M)) = sumi=0 to s ( XR ^i *Y T1(b(i)) )
where b(i) are matrices over the ring  , so T1(b(i)) are constant
polynomial matrices. , so T1(b(i)) are constant
polynomial matrices.
This step corresponds to (3) in Wikipedia. In contrast to Wikipedia, we
write  as finite sum of not exactly determined number of summands,
which may be greater than needed (including summands of value 0). This
will be sufficient to provide a representation of as finite sum of not exactly determined number of summands,
which may be greater than needed (including summands of value 0). This
will be sufficient to provide a representation of      as
infinite, but finitely supported sum, see step 3. as
infinite, but finitely supported sum, see step 3.
- Write
     , the product of the characteristic matrix and its
adjugate as finite sum of scaled monomials, see cpmadugsumfi 20682. This
representation is obtained by replacing , the product of the characteristic matrix and its
adjugate as finite sum of scaled monomials, see cpmadugsumfi 20682. This
representation is obtained by replacing  by the representation
resulting from step 1. and performing calculation rules available for the
associative algebra of matrices over polynomials over a commutative ring: by the representation
resulting from step 1. and performing calculation rules available for the
associative algebra of matrices over polynomials over a commutative ring:
cm(M) *Y adj(cm(M))
= sumi=0 to s ( XR ^i *Y ( T1(b(i-1))
- T1(M) xY T1(b(i)) ) )
+ XR ^(s+1) *Y ( T1(b(s)) - T1(M) xY T1(b(0))
where b(i) are matrices over  , so T1(b(i)) are constant polynomial
matrices: , so T1(b(i)) are constant polynomial
matrices:
cm(M) *Y adj(cm(M))
= cm(M) *Y sumi=0 to s ( XR ^i *Y T1(b(i)) )
[see pmatcollpw3fi1 20593 (step 1.)]
= ( ( XA *Y 1Y ) - T1(M) )
*Y sumi=0 to s ( XR ^i *Y T1(b(i)) )
[def. of cm(M)]
= ( XA *Y 1Y ) *Y sumi=0 to s ( XR ^i *Y T1(b(i)) )
- T1(M) *Y sumi=0 to s ( XR ^i *Y T1(b(i)) )
[see rngsubdir 18600]
= sumi=0 to s ( XR ^i *Y ( T1(b(i-1))
- T1(M) xY T1(b(i)) ) )
+ XR ^(s+1) *Y ( T1(b(s)) - T1(M) xY T1(b(0))
[see cpmadugsumlemF 20681]
This step corresponds partially to (4) in Wikipedia.
- Write
     as infinite, but finitely supported sum of scaled
monomials, see cpmadugsum 20683: as infinite, but finitely supported sum of scaled
monomials, see cpmadugsum 20683:
cm(M) * adj(cm(M)) = sumi ( XR ^i *Y G(i) )
This representation is obtained by defining a function G for the
coefficients, which we call "characteristic factor function", see
chfacfisf 20659, which covers the special terms and the padding with 0.
G(i) is a constant polynomial matrix (see chfacfisfcpmat 20660). This step
corresponds partially to (4) in Wikipedia, with summands of value 0
added.
- Write
       , the scalar matrix (diagonal matrix) with
the characteristic polynomial of a matrix as diagional elements, as
infinite, but finitely supported sum of scaled monomials. See
cpmidgsum 20673: , the scalar matrix (diagonal matrix) with
the characteristic polynomial of a matrix as diagional elements, as
infinite, but finitely supported sum of scaled monomials. See
cpmidgsum 20673:
p(m) *Y IY = sumi ( XR ^i *Y ( S(pi) *Y IY ) )
The proof of cpmidgsum 20673 is making use of pmatcollpwscmat 20596, because
       is a scalar/diagonal polynomial matrix with the
characteristic polynomial "p(M)" as diagonal entries (since pi is
an element of the ring is a scalar/diagonal polynomial matrix with the
characteristic polynomial "p(M)" as diagonal entries (since pi is
an element of the ring  , S(pi) is a (constant) polynomial). This
corresponds to (5) in Wikipedia, with summands of value 0 added. , S(pi) is a (constant) polynomial). This
corresponds to (5) in Wikipedia, with summands of value 0 added.
- Transform the sum representation of
     from step 3. into
polynomials over matrices: from step 3. into
polynomials over matrices:
T2(cm(M) * adj(cm(M))) = sumi ( U(G(i)) *Q XA ^i )
[see cpmadumatpoly 20688]
where U(G(i)) is a matrix over the ring  . .
- Transform the sum representation of
 from step 4. into polynomials
over matrices: from step 4. into polynomials
over matrices:
T2(p(m) *Y IY) = sumi ( pi *A IA ) *Q XA ^i )
[see cpmidpmat 20678]
- Equate the sum representations resulting from steps 5. and 6. by using
cpmadurid 20672 to obtain the equation
sumi ( U(G(i)) *Q XA ^i ) = sumi ( pi *A IA ) *Q XA ^i ):
sumi ( U(G(i)) *Q XA ^i )
= T2(cm(M) * adj(cm(M))) [see step 5.]
= T2(p(m) *Y IY) [see cpmadurid 20672]
= sumi ( pi *A IA ) *Q XA ^i ) [see step 6.]
Note that this step is contained in the proof of chcoeffeq 20691, see
step 9. This step corresponds to the conclusion from (4) and (5)
in Wikipedia, with summands of value 0 added.
- Compare the sum representations of step 7. to obtain the equations
U(G(i)) = pi *A IA , see chcoeffeqlem 20690. This corresponds to (6) in
Wikipedia. Since the coefficients of the transformed representations and
the original representations are identical, the equations of the
coefficients are also valid for the original representations of steps 3.
and 4.
- Multiply the equations of the coefficients from step 8. from the left by
M^i, and sum up, see chcoeffeq 20691:
sumi ( M^i xA U(G(i)) ) = sumi ( M^i xA ( pi *A IA) )
This corresponds to (7) in Wikipedia.
- Transform the right hand side of the equation in step 9. into an
appropriate form, see cayhamlem3 20692:
sumi ( pi *A M^i )
= sumi ( M^i xA ( pi *A IA) ) [see cayhamlem2 20689]
= sumi ( M^i xA U(G(i)) ) [see chcoeffeq 20691]
- Apply the theorem for telescoping sums, see telgsumfz 18387, to the sum
sumi ( T1(M)^i xY G(i) ), which results in an equation to 0:
sumi ( T1(M)^i xY G(i) ) = 0Y, see cayhamlem1 20671:
sumi ( T1(M)^i xY G(i) )
= sumi=1 to s
( T1(M)^i xY T1(b(i-1)) - T1(M)^(i+1) xY T1(b(i)) )
+ ( T1(M)^(s+1) xY T1(b(s)) - T1(M) xY T1(b(0)) )
[see chfacfpmmulgsum2 20670]
= ( T1(M) xY T1(b(0)) - T1(M)^(s+1) xY T1(b(s)) )
+ ( T1 M)^(s+1) xY T1(b(s)) - T1(M) xY T1(b(0)) )
[see telgsumfz 18387]
= 0Y [see grpnpncan0 17511]
This step corresponds partially to (8) in Wikipedia.
- Since
 is a ring homomorphism (see mat2pmatrhm 20539), the left hand
side of the equation in step 10. can be transformed into a representation
appropriate to apply the result of step 11., see cayhamlem4 20693: is a ring homomorphism (see mat2pmatrhm 20539), the left hand
side of the equation in step 10. can be transformed into a representation
appropriate to apply the result of step 11., see cayhamlem4 20693:
sumi ( pi *A M^i )
= sumi ( M^i xA U(G(i)) ) [see cayhamlem3 20692 (step 10.)]
= U(T1(sumi ( M^i xA U(G(i)) ))) [see m2cpminvid 20558]
= U(sumi T1( M^i xA U(G(i)) )) [see gsummptmhm 18340]
= U(sumi ( T1(M^i) xY T1(U(G(i))) )) [see rhmmul 18727]
= U(sumi ( T1(M)^i xY T1(U(G(i))) )) [see mhmmulg 17583]
= U(sumi ( T1(M)^i xY G(i) )) [see m2cpminvid2 20560 ]
- Finally, combine the results of steps 11. and 12., and use the fact that
 (and therefore also its inverse (and therefore also its inverse  ) is an injective ring
homomorphism (see mat2pmatf1 20534 and mat2pmatrhm 20539) to transform the
equality resulting from steps 11. and 12. into the desired equation
sumi ( pi *A M^i ) = 0A , see cayleyhamilton 20695 resp.
cayleyhamilton0 20694: ) is an injective ring
homomorphism (see mat2pmatf1 20534 and mat2pmatrhm 20539) to transform the
equality resulting from steps 11. and 12. into the desired equation
sumi ( pi *A M^i ) = 0A , see cayleyhamilton 20695 resp.
cayleyhamilton0 20694:
sumi ( pi *A M^i )
= U(sumi ( T1(M)^i xY G(i) )) [see cayhamlem4 20693 (step 12.)]
= U(0Y ) [see cayhamlem1 20671 (step 11.)]
= 0A [see m2cpminv0 20566]
The transformations in steps 5., 6., 10., 12. and 13. are not mentioned in the
proof provided in Wikipedia, since it makes no distinction between a matrix
over a ring  and its
representation as matrix over the polynomial ring
over the ring and its
representation as matrix over the polynomial ring
over the ring  in
general! in
general!
|
| |
| Theorem | cpmadurid 20672 |
The right-hand fundamental relation of the adjugate (see madurid 20450)
applied to the characteristic matrix of a matrix. (Contributed by AV,
25-Oct-2019.)
|
     Mat Mat                  CharPlyMat CharPlyMat
       Poly1 Poly1         Mat Mat      
 var1 var1         matToPolyMat matToPolyMat     
                                               maAdju maAdju
                                           
    |
| |
| Theorem | cpmidgsum 20673* |
Representation of the identity matrix multiplied with the characteristic
polynomial of a matrix as group sum. (Contributed by AV,
7-Nov-2019.)
|
     Mat Mat                 Poly1 Poly1         Mat Mat      
 var1 var1      
 .g .g  mulGrp mulGrp                           algSc algSc         CharPlyMat CharPlyMat               
                           g g           
       coe1 coe1      
       |
| |
| Theorem | cpmidgsumm2pm 20674* |
Representation of the identity matrix multiplied with the characteristic
polynomial of a matrix as group sum with a matrix to polynomial matrix
transformation. (Contributed by AV, 13-Nov-2019.)
|
     Mat Mat                 Poly1 Poly1         Mat Mat      
 var1 var1      
 .g .g  mulGrp mulGrp                           algSc algSc         CharPlyMat CharPlyMat               
                             matToPolyMat matToPolyMat                         g g           
       coe1 coe1              |
| |
| Theorem | cpmidpmatlem1 20675* |
Lemma 1 for cpmidpmat 20678. (Contributed by AV, 13-Nov-2019.)
|
     Mat Mat                 Poly1 Poly1         Mat Mat      
 var1 var1      
 .g .g  mulGrp mulGrp                           algSc algSc         CharPlyMat CharPlyMat               
                             matToPolyMat matToPolyMat               coe1 coe1     
                    coe1 coe1          |
| |
| Theorem | cpmidpmatlem2 20676* |
Lemma 2 for cpmidpmat 20678. (Contributed by AV, 14-Nov-2019.) (Proof
shortened by AV, 7-Dec-2019.)
|
     Mat Mat                 Poly1 Poly1         Mat Mat      
 var1 var1      
 .g .g  mulGrp mulGrp                           algSc algSc         CharPlyMat CharPlyMat               
                             matToPolyMat matToPolyMat               coe1 coe1     
                             |
| |
| Theorem | cpmidpmatlem3 20677* |
Lemma 3 for cpmidpmat 20678. (Contributed by AV, 14-Nov-2019.) (Proof
shortened by AV, 7-Dec-2019.)
|
     Mat Mat                 Poly1 Poly1         Mat Mat      
 var1 var1      
 .g .g  mulGrp mulGrp                           algSc algSc         CharPlyMat CharPlyMat               
                             matToPolyMat matToPolyMat               coe1 coe1     
                      finSupp finSupp       |
| |
| Theorem | cpmidpmat 20678* |
Representation of the identity matrix multiplied with the characteristic
polynomial of a matrix as polynomial over the ring of matrices.
(Contributed by AV, 14-Nov-2019.) (Revised by AV, 7-Dec-2019.)
|
     Mat Mat                 Poly1 Poly1         Mat Mat      
 var1 var1      
 .g .g  mulGrp mulGrp                           algSc algSc         CharPlyMat CharPlyMat               
                             matToPolyMat matToPolyMat                 Poly1 Poly1        var1 var1               
 .g .g  mulGrp mulGrp          pMatToMatPoly
pMatToMatPoly         
               
   g g   
      coe1 coe1     
             |
| |
| Theorem | cpmadugsumlemB 20679* |
Lemma B for cpmadugsum 20683. (Contributed by AV, 2-Nov-2019.)
|
     Mat Mat                 Poly1 Poly1         Mat Mat      
  matToPolyMat matToPolyMat        var1 var1      
 .g .g  mulGrp mulGrp                                      
                            
        
 g g                                  g g                
                 |
| |
| Theorem | cpmadugsumlemC 20680* |
Lemma C for cpmadugsum 20683. (Contributed by AV, 2-Nov-2019.)
|
     Mat Mat                 Poly1 Poly1         Mat Mat      
  matToPolyMat matToPolyMat        var1 var1      
 .g .g  mulGrp mulGrp                                      
                            
        
 g g                                  g g                                      |
| |
| Theorem | cpmadugsumlemF 20681* |
Lemma F for cpmadugsum 20683. (Contributed by AV, 7-Nov-2019.)
|
     Mat Mat                 Poly1 Poly1         Mat Mat      
  matToPolyMat matToPolyMat        var1 var1      
 .g .g  mulGrp mulGrp                                    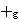       
            
              
   
                 
   g g                                         g g             
                      g g                         
           
                        
                                  |
| |
| Theorem | cpmadugsumfi 20682* |
The product of the characteristic matrix of a given matrix and its
adjunct represented as finite sum. (Contributed by AV, 7-Nov-2019.)
(Proof shortened by AV, 29-Nov-2019.)
|
     Mat Mat                 Poly1 Poly1         Mat Mat      
  matToPolyMat matToPolyMat        var1 var1      
 .g .g  mulGrp mulGrp                                    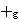       
                            maAdju maAdju
                                                 g g  
                      
           
                        
                                  |
| |
| Theorem | cpmadugsum 20683* |
The product of the characteristic matrix of a given matrix and its
adjunct represented as an infinite sum. (Contributed by AV,
10-Nov-2019.)
|
     Mat Mat                 Poly1 Poly1         Mat Mat      
  matToPolyMat matToPolyMat        var1 var1      
 .g .g  mulGrp mulGrp                                    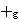       
                            maAdju maAdju
                  
    
    
                     
                       
             
           
                                                              g g    
    
            |
| |
| Theorem | cpmidgsum2 20684* |
Representation of the identity matrix multiplied with the
characteristic polynomial of a matrix as another group sum.
(Contributed by AV, 10-Nov-2019.)
|
     Mat Mat                 Poly1 Poly1         Mat Mat      
  matToPolyMat matToPolyMat        var1 var1      
 .g .g  mulGrp mulGrp                                    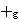       
                            maAdju maAdju
                  
    
    
                     
                       
             
           
                      CharPlyMat CharPlyMat               
                                           g g  
      
            |
| |
| Theorem | cpmidg2sum 20685* |
Equality of two sums representing the identity matrix multiplied with
the characteristic polynomial of a matrix. (Contributed by AV,
11-Nov-2019.)
|
     Mat Mat                 Poly1 Poly1         Mat Mat      
  matToPolyMat matToPolyMat        var1 var1      
 .g .g  mulGrp mulGrp                                    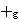       
                            maAdju maAdju
                  
    
    
                     
                       
             
           
                      CharPlyMat CharPlyMat               
 algSc algSc                                       g g           
       coe1 coe1                 g g    
    
            |
| |
| Theorem | cpmadumatpolylem1 20686* |
Lemma 1 for cpmadumatpoly 20688. (Contributed by AV, 20-Nov-2019.)
(Revised by AV, 15-Dec-2019.)
|
     Mat Mat                 Poly1 Poly1         Mat Mat      
  matToPolyMat matToPolyMat      
       
                      
    
    
                     
                       
             
           
                      ConstPolyMat ConstPolyMat     
                    var1 var1          
               maAdju maAdju                 Poly1 Poly1        var1 var1               
 .g .g  mulGrp mulGrp          cPolyMatToMat
cPolyMatToMat                                       
  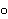          |
| |
| Theorem | cpmadumatpolylem2 20687* |
Lemma 2 for cpmadumatpoly 20688. (Contributed by AV, 20-Nov-2019.)
(Revised by AV, 15-Dec-2019.)
|
     Mat Mat                 Poly1 Poly1         Mat Mat      
  matToPolyMat matToPolyMat      
       
                      
    
    
                     
                       
             
           
                      ConstPolyMat ConstPolyMat     
                    var1 var1          
               maAdju maAdju                 Poly1 Poly1        var1 var1               
 .g .g  mulGrp mulGrp          cPolyMatToMat
cPolyMatToMat                                       
  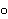   finSupp finSupp       |
| |
| Theorem | cpmadumatpoly 20688* |
The product of the characteristic matrix of a given matrix and its
adjunct represented as a polynomial over matrices. (Contributed by AV,
20-Nov-2019.) (Revised by AV, 7-Dec-2019.)
|
     Mat Mat                 Poly1 Poly1         Mat Mat      
  matToPolyMat matToPolyMat      
       
                      
    
    
                     
                       
             
           
                      ConstPolyMat ConstPolyMat     
                    var1 var1          
               maAdju maAdju                 Poly1 Poly1        var1 var1               
 .g .g  mulGrp mulGrp          cPolyMatToMat
cPolyMatToMat         pMatToMatPoly
pMatToMatPoly         
                                           g g    
                     |
| |
| Theorem | cayhamlem2 20689 |
Lemma for cayhamlem3 20692. (Contributed by AV, 24-Nov-2019.)
|
              Mat Mat                                   .g .g  mulGrp mulGrp       
            
              
         
        
        
        
     |
| |
| Theorem | chcoeffeqlem 20690* |
Lemma for chcoeffeq 20691. (Contributed by AV, 21-Nov-2019.) (Proof
shortened by AV, 7-Dec-2019.) (Revised by AV, 15-Dec-2019.)
|
     Mat Mat                 Poly1 Poly1         Mat Mat              
                     matToPolyMat matToPolyMat         CharPlyMat CharPlyMat               
                   
                
                                    
           
                                                 cPolyMatToMat
cPolyMatToMat             
             
               Poly1 Poly1    g g                    Poly1 Poly1       .g .g  mulGrp mulGrp  Poly1 Poly1      var1 var1          Poly1 Poly1    g g    
     coe1 coe1     
       Poly1 Poly1       .g .g  mulGrp mulGrp  Poly1 Poly1      var1 var1         
               coe1 coe1           |
| |
| Theorem | chcoeffeq 20691* |
The coefficients of the characteristic polynomial multiplied with the
identity matrix represented by (transformed) ring elements obtained from
the adjunct of the characteristic matrix. (Contributed by AV,
21-Nov-2019.) (Proof shortened by AV, 8-Dec-2019.) (Revised by AV,
15-Dec-2019.)
|
     Mat Mat                 Poly1 Poly1         Mat Mat              
                     matToPolyMat matToPolyMat         CharPlyMat CharPlyMat               
                   
                
                                    
           
                                                 cPolyMatToMat
cPolyMatToMat         
                            
              coe1 coe1          |
| |
| Theorem | cayhamlem3 20692* |
Lemma for cayhamlem4 20693. (Contributed by AV, 24-Nov-2019.)
(Revised
by AV, 15-Dec-2019.)
|
     Mat Mat                 Poly1 Poly1         Mat Mat              
                     matToPolyMat matToPolyMat         CharPlyMat CharPlyMat               
                   
                
                                    
           
                                                 cPolyMatToMat
cPolyMatToMat        .g .g  mulGrp mulGrp       
                                         g g         coe1 coe1        
          g g           
              |
| |
| Theorem | cayhamlem4 20693* |
Lemma for cayleyhamilton 20695. (Contributed by AV, 25-Nov-2019.)
(Revised by AV, 15-Dec-2019.)
|
     Mat Mat                 Poly1 Poly1         Mat Mat              
                     matToPolyMat matToPolyMat         CharPlyMat CharPlyMat               
                   
                
                                    
           
                                                 cPolyMatToMat
cPolyMatToMat        .g .g  mulGrp mulGrp         .g .g  mulGrp mulGrp          
                             g g         coe1 coe1        
             g g               
           |
| |
| Theorem | cayleyhamilton0 20694* |
The Cayley-Hamilton theorem: A matrix over a commutative ring
"satisfies its own characteristic equation". This version of
cayleyhamilton 20695 provides definitions not used in the theorem
itself,
but in its proof to make it clearer, more readable and shorter compared
with a proof without them (see cayleyhamiltonALT 20696)! (Contributed by
AV, 25-Nov-2019.) (Revised by AV, 15-Dec-2019.)
|
     Mat Mat                        
                   .g .g  mulGrp mulGrp          CharPlyMat CharPlyMat        coe1 coe1            Poly1 Poly1         Mat Mat                                            .g .g  mulGrp mulGrp          matToPolyMat matToPolyMat               
   
                                                                  
                            cPolyMatToMat cPolyMatToMat                       g g           
            |
| |
| Theorem | cayleyhamilton 20695* |
The Cayley-Hamilton theorem: A matrix over a commutative ring
"satisfies its own characteristic equation", see theorem 7.8
in [Roman]
p. 170 (without proof!), or theorem 3.1 in [Lang] p. 561. In other
words, a matrix over a commutative ring "inserted" into its
characteristic polynomial results in zero. This is Metamath 100 proof
#49. (Contributed by Alexander van der Vekens, 25-Nov-2019.)
|
     Mat Mat                           CharPlyMat CharPlyMat        coe1 coe1                     .g .g  mulGrp mulGrp                        g g           
            |
| |
| Theorem | cayleyhamiltonALT 20696* |
Alternate proof of cayleyhamilton 20695, the Cayley-Hamilton theorem.
This proof does not use cayleyhamilton0 20694 directly, but has the same
structure as the proof of cayleyhamilton0 20694. In contrast to the
proof of cayleyhamilton0 20694, only the definitions required to
formulate the theorem itself are used, causing the definitions used in
the lemmas being expanded, which makes the proof longer and more
difficult to read. (Contributed by AV, 25-Nov-2019.)
(New usage is discouraged.) (Proof modification is discouraged.)
|
     Mat Mat                           CharPlyMat CharPlyMat        coe1 coe1                     .g .g  mulGrp mulGrp                        g g           
            |
| |
| Theorem | cayleyhamilton1 20697* |
The Cayley-Hamilton theorem: A matrix over a commutative ring
"satisfies its own characteristic equation", or, in other
words, a
matrix over a commutative ring "inserted" into its
characteristic
polynomial results in zero. In this variant of cayleyhamilton 20695, the
meaning of "inserted" is made more transparent: If the
characteristic
polynomial is a polynomial with coefficients      , then a
matrix over a commutative ring "inserted" into its
characteristic
polynomial is the sum of these coefficients multiplied with the
corresponding power of the matrix. (Contributed by AV, 25-Nov-2019.) , then a
matrix over a commutative ring "inserted" into its
characteristic
polynomial is the sum of these coefficients multiplied with the
corresponding power of the matrix. (Contributed by AV, 25-Nov-2019.)
|
     Mat Mat                           CharPlyMat CharPlyMat        coe1 coe1                     .g .g  mulGrp mulGrp                  var1 var1        Poly1 Poly1               
 .g .g  mulGrp mulGrp                    
              
     finSupp finSupp          
    g g           
             g g           
             |
| |
| PART 12 BASIC TOPOLOGY
|
| |
| 12.1 Topology
|
| |
| 12.1.1 Topological spaces
A topology on a set is a set of subsets of that set, called open sets, which
satisfy certain conditions. One condition is that the whole set be an open
set. Therefore, a set is recoverable from a topology on it (as its union,
see toponuni 20719), and it may sometimes be more convenient to
consider
topologies without reference to the underlying set. This is why we define
successively the class of topologies (df-top 20699), then the function which
associates with a set the set of topologies on it (df-topon 20716), and finally
the class of topological spaces, as extensible structures having an
underlying set and a topology on it (df-topsp 20737). Of course, a topology is
the same thing as a topology on a set (see toprntopon 20729).
|
| |
| 12.1.1.1 Topologies
|
| |
| Syntax | ctop 20698 |
Syntax for the class of topologies.
|
 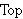 |
| |
| Definition | df-top 20699* |
Define the class of topologies. It is a proper class (see topnex 20800).
See istopg 20700 and istop2g 20701 for the corresponding characterizations,
using respectively binary intersections like in this definition and
nonempty finite intersections.
The final form of the definition is due to Bourbaki (Def. 1 of
[BourbakiTop1] p. I.1), while the
idea of defining a topology in terms
of its open sets is due to Aleksandrov. For the convoluted history of
the definitions of these notions, see
Gregory H. Moore, The emergence of open sets, closed sets, and limit
points in analysis and topology, Historia Mathematica 35 (2008)
220--241.
(Contributed by NM, 3-Mar-2006.) (Revised by BJ, 20-Oct-2018.)
|
 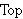 
            
    
             |
| |
| Theorem | istopg 20700* |
Express the predicate " is a topology." See istop2g 20701 for another
characterization using nonempty finite intersections instead of binary
intersections. is a topology." See istop2g 20701 for another
characterization using nonempty finite intersections instead of binary
intersections.
Note: In the literature, a topology is often represented by a
calligraphic letter T, which resembles the letter J. This confusion may
have led to J being used by some authors (e.g., K. D. Joshi,
Introduction to General Topology (1983), p. 114) and it is
convenient
for us since we later use  to represent linear transformations
(operators). (Contributed by Stefan Allan, 3-Mar-2006.) (Revised by
Mario Carneiro, 11-Nov-2013.) to represent linear transformations
(operators). (Contributed by Stefan Allan, 3-Mar-2006.) (Revised by
Mario Carneiro, 11-Nov-2013.)
|
     |